Sn、Cu掺杂的β-Ga₂O₃能带的理论计算

Theoretical Calculation of Energy Band on β-Ga₂O₃ Doped with Sn and Cu elements

摘要: 本文基于MS 2018软件，采用密度泛函第一性原理方法，利用平面波超软赝势计算了β-Ga₂O₃超胞掺杂不同含量Sn、Cu元素后的能带结构、态密度和分波态密度变化特性。研究发现，在本征半导体β-Ga₂O₃超胞中进行少量的Sn、Cu元素掺杂均可减小β-Ga₂O₃的禁带宽度，增强其导电特性。少量Sn掺杂后，β-Ga₂O₃的费米能级更接近导带，表现出更明显的n型导电特性，且其费米面附近的态密度明显增加。而少量Cu掺杂后，价带上部还出现了浅受主能级，导致β-Ga₂O₃的费米能级更接近其价带，具有明显的p型导电特性。对比研究发现，掺杂浓度越高，费米面附近的态密度增加效果就越强，这更有利于β-Ga₂O₃半导体用于制备各类异质结晶体管和光电器件领域中。

Abstract: Based on plane-wave ultra-soft pseudopotential model in the MS 2018 software, the energy band structure, density of states and partial density of the intrinsic β-Ga₂O₃ and β-Ga₂O₃ doped with different contents of Sn and Cu elements were calculated by using the first-principles calculation method. The results show that a small amount of substituted Sn and Cu atoms doping in the intrinsic β-Ga₂O₃ supercell lattice structure can reduce the bandgap width and the conductivity of β-Ga₂O₃ can be improved. Doped with a small amount of Sn elements, the Fermi energy level of Sn/β-Ga₂O₃ moves forward to the conduction band bottom, showing more obvious n-type conductivity, and the density of states near the Fermi energy level increases obviously. However, doped with a small amount of Cu elements, the Fermi energy level of Cu/β-Ga₂O₃ is closer to the top of the valence band and the shallow donor impurity energy level is introduced into the top of the valence band, showing an obvious p-type conductivity. All the calculation results indicate that the higher the doping concentration is, the stronger the effect of increasing the density of states near the Fermi energy level is, which is more favorable for β-Ga₂O₃ semiconductor to be used in the preparation of various heterojunction transistors and optoelectronic devices.

1. 引言

β-Ga₂O₃半导体的禁带宽度约为4.8 eV，其在可见区260 nm的紫外区都有较好的光学通过率，加上其制造成本较低、具有较高的击穿电场强度和较快的载流子传输率等优点，是制备工作在短波长的光电子器件的首选材料。近年来，世界各国科学家都对β-Ga₂O₃的物理性质和制备技术开展了一系列的研究，特别是对β-Ga₂O₃的电子特性、光学以及磁学特性研究中，更是投入了大量的资金和精力 [1] [2] [3]。但因本征的β-Ga₂O₃半导体电导率不高，要将其应用于日盲型紫外探测器和其它短波长光电器件，就必需制备出电导率满足半导体器件应用要求的n型和p型β-Ga₂O₃材料。

掺杂改性是提高半导体材料光电性能的有效途径，通过少量的元素掺杂，可显著改善半导体材料的吸收性、电导率和载流子迁移率 [4]。目前，通过掺杂不同元素，研究掺杂效应对β-Ga₂O₃能带、态密度和电导率影响的研究论文还不是特别多．针对将来应用需要及目前β-Ga₂O₃理论研究存在的问题，本文基于第一性原理的平面波超软赝势法，利用Material Studio 2018软件中的CASTEP模块，分别计算并比较了本征β-Ga₂O₃、Sn掺杂的Sn/β-Ga₂O₃和Cu掺杂的Cu/β-Ga₂O₃晶体超胞的能带结构、态密度和分波态密度，并对不同Sn、Cu掺杂百分比对β-Ga₂O₃晶体电导率的影响进行了理论计算。讨论了掺杂前后其能带结构、态密度和分波态密度的变化及影响因素 [5] [6]。研究结果可为新一代β-Ga₂O₃高迁移率半导体薄膜场效应晶体管和日盲型紫外探测器的制备和应用提供理论依据。

2. 理论模型和计算方法

基于第一性原理密度泛函理论(DFT)，采用CASTEP计算模块中的平面波赝势(PWPP)方法，根据MS 2018软件数据库中收录的cif文件中导入Ga₂O₃的晶体基本单元结构，构建了3 × 1 × 1的β-Ga₂O₃晶体超胞 [7] [8] [9] [10]，如图1所示。随后，对超胞进行了几何优化并进行了计算。计算中，采用一般能量的平面波赝势技术，基于平面波基函数展开了电子波函数，并选用超软赝势来描述Ga、O、Cu、Sn原子中电子与离子核的相互作用，使用广义梯度近似的Perdew、Burke和Ernzerhof (PBE)格式加上Hubbard U (GGA + U)来描述交换相关效应。最后，利用BFGS算法，实现了几何结构和原子坐标的完全松弛，通过测试估算其电子性能和几何结构的收敛性后，最后得到的优化后的真实计算参数如表1所示。

Table 1. Optimized calculation parameters

表1. 优化后采用的计算参数

Ga₂O₃分子可形成5种不同的晶体结构，通过对Ga₂O₃的这5种同份异构体的对比，我们发现单斜结构的β-Ga₂O₃具备更稳定的物理化学性质，而其他4种同份异构体在一定条件下均可以向β-Ga₂O₃转化。因此，β-Ga₂O₃相是最稳定常见的晶体构型。β-Ga₂O₃的晶体结构属于C2/m空间群，具有双旋转对称轴，基本结构单元为Ga₄O₂₄，是由两个GaO₄四面体和两个共棱的GaO₆八面体套构而成的。Ga原子在β-Ga₂O₃结构中有两个点位，分别为四面体中的Ga₍₁₎点位及八面体中的Ga₍₂₎点位。不同点位的Ga原子又被O原子包围。图1为1 × 1 × 1的β-Ga₂O₃的超胞结构，晶格参数为：a = 12.230 Å，b = 6.080 Å，c = 5.800 Å；α = γ = 90˚，β = 103.7˚，与实验值吻合较好，证明我们的实验是合理的。图上标注了处于四面体中心的Ga₍₁₎点位，处于八面体中心的Ga₍₂₎点位及3个表示为O₍₁₎，O₍₂₎，O₍₃₎的不同点位O原子的位置图。该超胞中，包括12个Ga原子和20个O原子。依照参考文献的结果，在计算中，当掺杂元素Sn或Cu原子替位Ga₍₂₎点位的Ga原子时，掺杂的β-Ga₂O₃晶格生成能为最低。因此，按照能量最低原理，本文研究了由Sn、Cu原子分替位取代β-Ga₂O₃晶格中的Ga₍₂₎点位Ga原子后的能带结构变化情况。

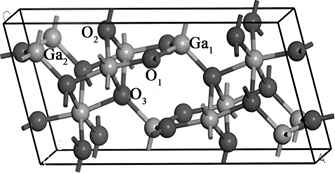
Figure 1. 1 × 1 ×1 lattice structure of β-Ga₂O₃ supercrystal cells and point location distribution of different atoms

图1. β-Ga₂O₃超晶胞1 × 1 × 1晶格结构及不同原子的点位分布图

3. 计算与讨论

图2给出了计算得到的本征β-Ga₂O₃超晶胞沿布里渊区特殊波矢对称点的能带结构图。其中，费米能级处于能量为0的位置。从计算得到的能带结构图中可看出，本征β-Ga₂O₃的导带处于费米面上方区域，价带位于费米面下方区域，价带顶部靠近费米面。其导带最低点和价带的最高点都位于布里渊区的同一波矢G点处，因此，本征β-Ga₂O₃为直接带隙半导体材料。从图2中还可看出，本征β-Ga₂O₃禁带宽度Eg约为1.98 eV，该能隙计算值与实际值4.23 eV有一定偏差，这主要是使用GGA的DFT理论计算时，是以基态为基础的，这将导致处于激发态电子之间的交换相关势被低估，最终使得理论计算得到的带隙值和实验带隙值有一定偏差 [7]。但在相同的计算条件下，其计算结果不影响对晶体电子能带结构的特性分析。虽然计算结果得出的能隙比实际值偏小。但这也能够说明本征β-Ga₂O₃的禁带能隙较大，电子迁移率不高，导电特性不能满足光电器件制备基本要求，要想使其实用化，必须开展本征β-Ga₂O₃半导体的n型和p型掺杂改性的研究。

Figure 2. The calculated band structure of the intrinsic β-Ga₂O₃ supercrystalline cell along the direction of the symmetry point in the Brillouin region. The corresponding points of transverse wave vector k are L(−0.5, 0, 0.5), M(−0.5, −0.5, 0.5), A(0, 0, 0.5), G(0, 0, 0), Z(0, −0.5, −0.5) and V(0, 0, 0.5), respectively

图2. 计算得到的本征β-Ga₂O₃超晶胞沿布里渊区对称点方向的能带结构图。横轴波矢k对应点分别为L(−0.5, 0, 0.5)，M(−0.5, −0.5, 0.5)，A(0, 0, 0.5)，G(0, 0, 0)，Z(0, −0.5, −0.5)和V(0, 0, 0.5)

为了进一步研究β-Ga₂O₃中电子能带的形成及分布特点，分别计算了β-Ga₂O₃的总态密度和分波态密度，图3(a)~(c)为计算得到的本征β-Ga₂O₃超晶胞的总态密度和分波态密度(DOS)的谱图。β-Ga₂O₃中的O、Ga的价电子态分别为2s²2p⁴和3d¹⁰4s²4p¹，从图3的分波态密度图中可看出，本征β-Ga₂O₃价带的上半部分主要由Ga原子的4p态、Ga原子的4s态和O原子的2p态轨道的成键态组成，宽度约为7.25 eV，处于费米能级以下0.00~7.50 eV能量范围。在价带的上部附近，O原子的2p态、Ga原子的4s和4p态存在广泛的重叠，表明它们之间存在强耦合。因此，Ga原子和O原子之间的原子键就表现出了较强烈的共价特性。从图3(a)中还可看到，β-Ga₂O₃半导体的价带中还存在−11.00~−13.00 eV和−16.00~−18.00 eV之间的中间价带和最低价带。其中，−11.00~−13.00 eV间的中间价带主要来自Ga原子3d能级及Ga原子与O原子的p轨道和s轨道电子的共同贡献。考虑到半导体的主要特性应是由价带顶部和导带底的位置决定的，因此，我们只需重点关注价带顶，导带低的结构特征，不需要深入讨论中间价带和最低价带。对比图3(a)~(c)的β-Ga₂O₃半导体的导带低能带分布，发现，其导带底能带主要由Ga原子的4s态组成，O原子的2p态和Ga原子的4p态也有一定的贡献。

Figure 3. Total and partial density of states of β-Ga₂O₃

图3. β-Ga₂O₃总态密度及分波态密度图

为研究n型及p型β-Ga₂O₃半导体的制备方法，我们首先计算了当一个及两个Sn原子替代Ga₍₂₎点位原子形成掺杂Sn/β-Ga₂O₃半导体能带结构。此时，掺杂Sn原子的比例占超胞总原子数的数值比分别为1:20和2:20。图4及图5分别给出了两种掺杂比例的计算能带结构图，O、Ga和Sn原子的价电子态排布规律分别为2s²2p⁴，3d¹⁰4s²4p¹和5s²5p²。结果表明，掺杂比例为1:20的Sn/β-Ga₂O₃的带隙Eg从本征材料的1.98 eV减小到1.37 eV，掺杂比例为2:20的2Sn/β-Ga₂O₃的Eg减小到1.46 eV。说明，Sn原子的掺杂将会使其禁带宽度明显减小。Sn掺杂后，其导带的最小值和价带的最大值都存在，且在G点处具有直接带隙。对比图4和图5能带结构特点，可看出，随着Sn元素掺杂比例的增大，费米面附近的态密度也随之增大。掺杂后，费米面明显上移，并与导带能级交迭，这将使其导电性得到进一步提高。此结果与文献研究结论一致，说明Sn掺杂可使β-Ga₂O₃成为n型半导体，并可应用在β-Ga₂O₃半导体材料的光电器件的制备中。

Figure 4. Energy band structure of Sn/β-Ga₂O₃ supercrystalline cells along the direction of symmetry point in the Brillouin region. Transverse wave vector k corresponding points of Z(0, 0, 0.5), G(0, 0, 0), Y(0, 0.5, 0), A(0.5, 0, 0), B(−0.5, 0, 0), D(−0.5, 0, 0.5), E(−0.5, 0.5, 0.5) and C(0, 0.5, 0.5), respectively

图4. Sn/β-Ga₂O₃超晶胞沿布里渊区对称点方向的能带结构图。横轴波矢k对应点分别为Z(0, 0, 0.5)，G(0, 0, 0)，Y(0, 0.5, 0)，A(0.5, 0, 0)，B(−0.5, 0, 0)，D(−0.5, 0, 0.5)，E(−0.5, 0.5, 0.5)和C(0, 0.5, 0.5)

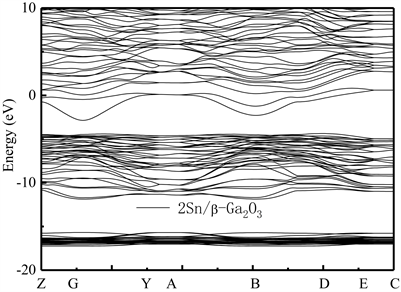
Figure 5. The band structure of 2Sn/β-Ga₂O₃ supercrystalline cells along the direction of the symmetry point in the Brillouin region. Transverse wave vector k corresponding points of Z(0, 0, 0.5), G(0, 0, 0), Y(0, 0.5, 0), A(0.5, 0, 0), B(−0.5, 0, 0), D(−0.5, 0, 0.5), E(−0.5, 0.5, 0.5) and C(0, 0.5, 0.5), respectively

图5. 2Sn/Ga₂O₃超晶胞沿布里渊区对称点方向的能带结构图。横轴波矢k对应点分别为Z(0, 0, 0.5)，G(0, 0, 0)，Y(0, 0.5, 0)，A(0.5, 0, 0)，B(−0.5, 0, 0)，D(−0.5, 0, 0.5)，E(−0.5, 0.5, 0.5)和C(0, 0.5, 0.5)

图6为掺杂比例为2:20的2Sn/β-Ga₂O₃的总态密度图及分波态密度图，可看出，Sn的杂质能级位于β-Ga₂O₃导带下0.00 eV附近处，说明2:20比例Sn的替位掺杂可在β-Ga₂O₃导带的底部引入Sn的杂质能级，导致β-Ga₂O₃的费米能级与Sn杂质能级相交，这会进一步增强其n型导电特性。此时，其带隙宽度约为1.46 eV，掺杂后，其价带顶从0.00 eV附近下降到−4.50 eV附近。与本征β-Ga₂O₃相比，Sn掺杂的β-Ga₂O₃的价带也存在多个子带，价带的顶部和导带的底部主要由O原子的2p态和Sn原子的5s态组成。在费米能级以下−11.00 eV区域，Sn原子的5s态还出现了一个较强的尖峰，O原子的2p态和Sn原子的5s、5p态有广泛的重叠，表明O原子和Sn原子之间存在键合相互作用，在导带中也观察到O原子的2p态的贡献。

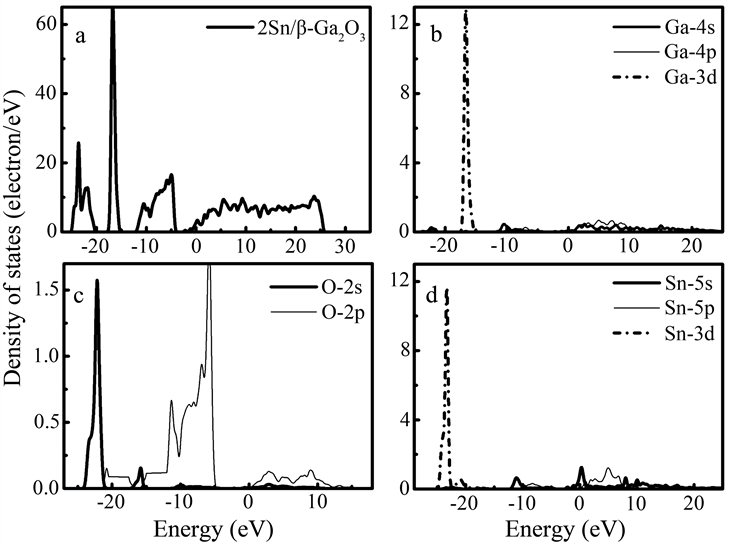
Figure 6. Total and partial density of states of Sn/β-Ga₂O₃ and it’s doping ratio is 2:20

图6. 掺杂比例为2:20的Sn/β-Ga₂O₃的总态密度及分波态密度图

为了比较不同掺杂元素对Ga₂O₃晶格能带结构的影响，并研究p型导电类型β-Ga₂O₃的制备技术，本文还研究了不同比例Cu元素替位Ga₍₂₎原子后的能带结构特点。图7和图8分别给出了掺杂比例分别为1:20和2:20的Cu/β-Ga₂O₃的能带结构图。可看到，掺杂后，Cu/β-Ga₂O₃能带结构的价带顶附近出现了新的较明显的受主能级，随着掺杂比例的增加，受主能级的态密度(DOS)也随之增大。这说明，Cu/β-Ga₂O₃明显为p型半导体。对比图7和图8还可看到，不同比例的Cu掺杂原子替代Ga₍₂₎点位Ga原子后，禁带宽度Eg从本征的约为1.98 eV分别减小为0.97 eV和1.12 eV，且体系的价带也明显上移，价带上还出现了浅受主能级。根据文献结论 [10] [11] [12]，此时，Cu掺杂后带隙窄化主要原因是O原子和Ga、Cu原子间较强的p-d杂化作用造成的。

Figure 7. Energy band structure of Cu/β-Ga₂O₃ supercrystalline cells along the direction of symmetry point in Brillouin region. Transverse wave vector k corresponding points of Z(0, 0, 0.5), G(0, 0, 0), Y(0, 0.5, 0), A(−0.5, 0.5, 0), B(−0.5, 0, 0), D(−0.5, 0, 0.5), E(−0.5, 0.5, 0.5), and C(0, 0.5, 0.5), respectively

图7. Cu/β-Ga₂O₃超晶胞沿布里渊区对称点方向的能带结构图。横轴波矢k对应点分别为Z(0, 0, 0.5)，G(0, 0, 0)，Y(0, 0.5, 0)，A(−0.5, 0.5, 0)，B(−0.5, 0, 0)，D(−0.5, 0, 0.5)，E(−0.5, 0.5, 0.5)和C(0, 0.5, 0.5)

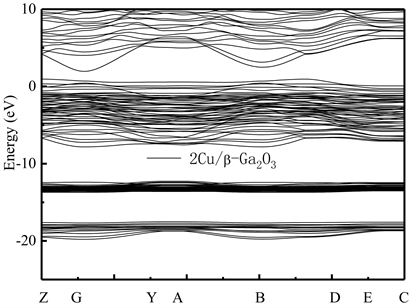
Figure 8. Energy band structure of Cu/β-Ga₂O₃ supercrystalline cells along the direction of symmetry point in Brillouin region. Transverse wave vector k corresponding points of Z(0, 0, 0.5),G(0, 0, 0),Y(0, 0.5, 0), A(−0.5, 0.5, 0), B(−0.5, 0, 0), D(−0.5, 0, 0.5), E(−0.5, 0.5, 0.5), and C(0, 0.5, 0.5), respectively

图8. 2Cu/Ga₂O₃超晶胞沿布里渊区对称点方向的能带结构图。横轴波矢k对应点分别为Z(0, 0, 0.5)，G(0, 0, 0)，Y(0, 0.5, 0)，A(−0.5, 0.5, 0)，B(−0.5, 0, 0)，D(−0.5, 0, 0.5)，E(−0.5, 0.5, 0.5)和C(0, 0.5, 0.5)

图9(a)~(d)给出了比例为2:20的Cu掺杂的2Cu/β-Ga₂O₃的态密度和分波态密度能带图。依照轨道理论，Cu、O、Ga原子的价电子态分别为3p⁶3d¹⁰4s¹、2s²2p⁴、3d¹⁰4s²4p¹。对比图9(a)和图9(d)的态密度图可知，Cu的受体杂质能级位于β-Ga₂O₃价带1.28~2.00 eV附近区域，与本征β-Ga₂O₃相比，2Cu/β-Ga₂O₃的价带顶主要由O原子的2p态和Cu原子的3d态的成键态构成，导带底主要由Cu原子的4s态、3p态以及Ga原子的4s轨道的成键态组合构成，但O原子的2p态也有少许贡献。在2Cu/β-Ga₂O₃晶体的费米能级附近，O原子的2p态和Cu原子的3d态有明显的重叠，表明它们之间存在很强的交换相互作用，这一强交换相互作用最终导致了费米能级附近能级出现劈裂，其费米能级更加深入价带。计算表明，随着Cu掺杂量的增加，2Cu/β-Ga₂O₃的p型导电特性更加显著 [11]。

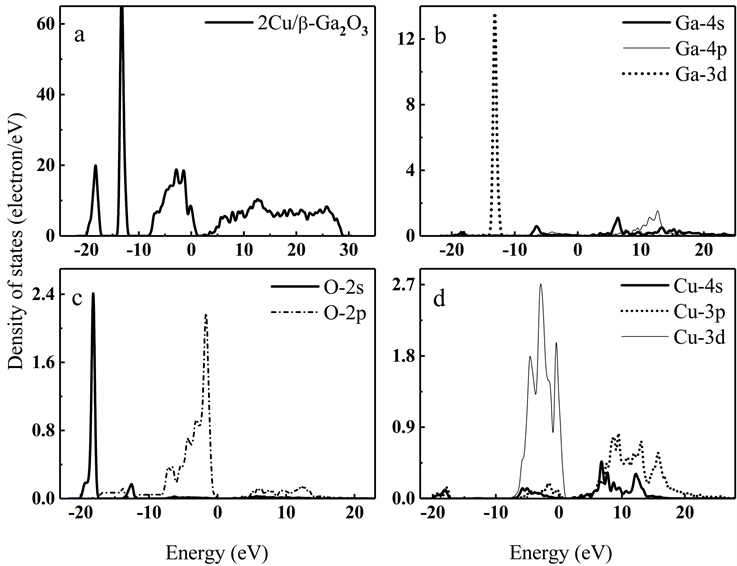
Figure 9. Total and partial density of states of Cu/β-Ga₂O₃ and the doping ratio of Cu elements is 2:20

图9. 掺杂比例为2:20的Cu/β-Ga₂O₃的总态密度及分波态密度图

4. 结论

Sn、Cu原子替位Ga₍₂₎原子点位的掺杂改性可调节本征β-Ga₂O₃的能带结构和导电类型。Sn的掺杂可在其导带底部引入杂质能级，导致β-Ga₂O₃的费米面出现明显上移，并使β-Ga₂O₃成为n型半导体，并随着Sn元素掺杂比例的增大，其禁带宽度逐渐减小，费米面附近的态密度也随之增大。Cu掺杂后，β-Ga₂O₃能带结构的价带顶附近出现了新的较明显的受主能级，随着掺杂比例的增大，其禁带宽度逐渐减小，费米面进入价带区，Cu受主杂质能级附近的态密度也随之增大。Cu掺杂后的Cu/β-Ga₂O₃明显为p型半导体。Sn、Cu原子替位Ga₍₂₎原子点位的掺杂改性可应用在β-Ga₂O₃半导体材料的光电器件的制备中。

基金项目

国家自然科学基金资助项目(61076104, 80220022)；

大连市科技创新基金资助重点项目(2019J12GX036)。

NOTES

^*通讯作者。