小车轨道踏面缺陷的多体动力学仿真

Multi-Body Dynamics Simulation of Tread Defects for Trolley Tracks

摘要: 轨道踏面缺陷是轨道式集装箱门式起重机(简称：轨道吊)上小车轨道缺陷的重要表现形式，准确分析小车轨道踏面的缺陷情况对保障轨道吊的安全运行至关重要。以广州港某轨道吊为研究对象，利用多体动力学软件RecurDyn对轨道踏面的有缺陷工况和无缺陷工况进行动力学仿真，获得两种工况下应力的分布以及小车车轮通过轨道时的振动加速度；将模拟获得的两种振动加速度进行对比分析，得出判断轨道缺陷的方法；将振动加速度的仿真结果与实测结果进行对比分析，验证了动力学仿真模型的可靠性。

Abstract: Rail tread defects, as a crucial manifestation form of trolley rail defects on rail container gantry crane (rail-mounted crane), being accurately analyzed is of great importance to ensure the safe operation of the rail-mounted gantry. Taking a rail-mounted gantry in Guangzhou port as the research object, utilizing multi-body dynamics software RecurDyn to perform dynamic simulation of the working condition on the two rail treads with or without defects, to get the stress distribution and vibration acceleration of the trolley wheels passing through the rail under the two different conditions. Through the analysis and contrast of the two kinds of vibration acceleration obtained by simulation, the method of judging rail defects was obtained. In addition, the simulation results of vibration acceleration were compared with the measured results to verify the reliability of the dynamic simulation model.

1. 引言

伴随着中国经济的快速发展，沿海港口的吞吐量逐年递增。轨道式集装箱门式起重机(简称：轨道吊)作为重要的装卸、搬运和堆放设备，在港口的应用越来越广。科学地评估轨道缺陷情况，有利于保障轨道吊安全运行，并预防重大事故发生。刚柔耦合多体动力学 [1] 有效地整合了刚体分析与柔体分析，将研究对象作为一个整体进行研究，所得结果具有更高的计算精度，且降低了仿真过程中的复杂度。

国内外学者采用刚柔耦合多体动力学进行了大量研究。贾尚帅和王兴民 [2] 建立内燃电传动车组动力包的刚柔耦合模型，通过研究，得到了中间构架柔性对带双子系统的双层隔振系统模态特性和谐响应的影响；桑平 [3] 建立刚柔耦合的弹性车轮轮对模型，对弹性车轮预装应力与静强度进行了计算分析，研究弹性车轮通过错牙时的车轮类型、轨缝长度、运行速度等参量对其动力学性能的影响；陈志平和祝男杰 [4] 采用多体动力学软件RecurDyn，建立了50 m大型射电天线轮轨接触刚柔耦合动力学模型并进行仿真，经与实验结果对比，验证了RecurDyn计算结果的可靠性；Kang Seokho [5] 利用RecurDyn分析辣椒收获机的动态特性并确定其不同条件下的安全工况；于凯 [6] 基于RecurDyn建立了刚柔耦合的厢式货车整车模型，考察了不同速度条件下车辆的平顺性。

本文基于多体动力学软件RecurDyn，采用刚柔耦合接触模型对小车轨道踏面进行数值模拟。对轨道踏面的有缺陷工况和无缺陷工况进行动力学仿真，模拟广州港某轨道吊上小车机构在轨道上的运行过程，得到车轮的振动加速度变化情况。本文的仿真结果可为小车轨道的日常维护和检修提供建议和预警。

2. 小车轨道刚柔耦合接触模型动力学仿真

2.1. 仿真算法基础

如果一个机械多体系统通过一系列最小的广义坐标 $y\left(t\right)$ 描述，运动方程就可以表示为一个二阶常微分方程，数学表达式为 [7]：

$M\left(y\right)\ddot{y}=f\left(y,\stackrel{\dot{}}{y},t\right)$ (1)

式中 $M\left(y\right)$ 为质量矩阵，包含所有体的质量特性和惯性特性；t为时间； $f\left(y,\stackrel{\dot{}}{y},t\right)$ 为外力和陀螺力的矢量。在给定t、y、 $\stackrel{\dot{}}{y}$ 的条件下，可对公式(1)采用多体系统的拓扑学有效求解出 $M{\left(y\right)}^{-1}f\left(y,\stackrel{\dot{}}{y},t\right)$。

2.2. 模型的简化原则

广州港某轨道吊由大车机构、小车机构、起升机构、控制室等子系统组成。由于轨道吊是一个非常复杂的系统，考虑计算成本及建模的复杂性，需要对本文研究的小车机构—轨道模型进行简化。轨道吊大梁下方四个立柱作为支撑整个横梁的结构，在模型中由约束条件代替；轨道吊上的楼梯和栏杆相对于钢结构而言质量很小，对整体结构应力的影响不大，可以不予考虑；另外，鉴于大车机构的作用是在地面轨道上缓慢移动起重机，对钢结构主体部分的影响较小，可以忽略；按照等效原则，将起升机构及小车机构的质量折算成荷载，施加在小车车轮上。

2.3. 有限元模型建立

本文通过三维CAD建模软件SolidWorks建立轨道吊的简化模型，并将模型以x-t格式导入多体动力学软件RecurDyn，如图1所示。由于本文主要研究轨道踏面的缺陷，为了简化模拟计算，将小车机构视为刚体，大梁及轨道视为柔性体。本文通过RecurDyn中的F-Flex模块对轨道建立柔性体模型，采用Shell单元对轨道及大梁进行网格划分，轨道踏面的网格尺寸为5 mm，其它部分的网格尺寸为150 mm。小车机构—无缺陷轨道的网格模型如图2所示。小车机构—有缺陷轨道的模型由图2的模型修改得到，利用HyperMesh软件将部分轨道踏面的节点向下移动0.5 mm，以便表征踏面缺陷。小车机构—有缺陷轨道的缺陷位置如图3所示。轨道吊为钢结构，主体结构的材料为Q345钢，辅材为Q235钢，弹性模量为210 GPa，泊松比0.3。

Figure 1. CAD model of trolley mechanism-track

图1. 小车机构–轨道的CAD模型

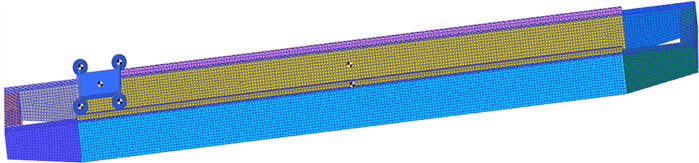
Figure 2. Finite element mesh of trolley mechanism-track

图2. 小车机构–轨道的有限元网格

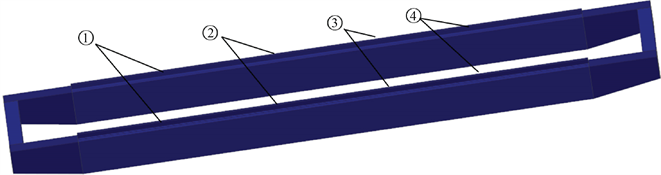
Figure 3. Location of the track defects

图3. 轨道缺陷的位置图

在RecurDyn中对模型进行约束设置，小车车轮施加旋转副，使车轮在轨道踏面上产生相对转动；小车机构与轨道踏面之间设置摩擦接触，使小车机构在轨道上水平移动并使车轮产生滚动；对大梁底面原四根立柱位置设置边界条件，约束其所有方向的平动自由度。

3. 小车在不同轨道上的动力学仿真分析

3.1. 轨道踏面缺陷简介

在轨道吊的生产过程中，由于施工时焊接不规范导致轨道连接处的踏面上出现许多缺陷；另外，随着使用年限的增长，轨道与车轮的摩擦(甚至啃轨)现象会持续影响轨道踏面的平整度，如图4所示。在实际工作条件下，车轮经过轨道踏面缺陷时，会发出刺耳的撞击声并产生显著的冲击。该情况会对车轮和轨道踏面造成伤害，如果不及时加以处理，甚至会发生断轨事故，造成人员伤亡及财产损失。因此本文通过仿真分析，对比车轮经过光滑轨道与预设缺陷轨道的振动加速度，考察轨道踏面缺陷与位置、严重程度的对应关系，为科学评估轨道缺陷位置及危害程度的方法提供理论依据。

Figure 4. Figure of defects of the track tread (the white part is the contact position of the wheel and the track; the red circle is the track tread defect)

图4. 轨道踏面的缺陷图(白色部位为车轮与轨道接触位置；红圈为轨道踏面缺陷)

3.2. 仿真过程与结果分析

根据现场实际测量的结果，车轮在轨道上行驶的角速度约为6 rad/s，据此可在RecurDyn软件中对车轮旋转副Revolute施加的驱动为-STEP (TIME, 0, 0, 0.2, 6)，仿真时间设定为10 s。由仿真结果可知，在两种工况下，大梁及轨道上应力分布和变形均随着小车的移动而变化，最大应力和变形出现在轨道中段。将小车运行在两种轨道下的力学性能进行对比分析，其结果如表1所示。

Table 1. Maximum stresses on the track under two working conditions

表1. 两种工况下轨道上的最大应力

由表1结果可知，有缺陷的轨道踏面所受的应力要大于光滑的轨道。该结果与工程实际情况相符，因为小车车轮滚过轨道踏面上的缺陷时两者会发生碰撞，产生较大的应力变化。两种轨道的应力云图如图5、图6所示，结果表明两种工况下轨道的最大应力皆远小于材料的屈服应力，本文的计算结果与帅飞 [8]、祁鹏 [9] 和王超 [10] 等人的结论相符，因此本文的仿真结果具有很好的可靠性，同时表明小车轨道处于安全状态。

Figure 5. Stress contour of smooth track

图5. 光滑轨道的应力云图

Figure 6. Stress contour of defective track

图6. 有缺陷轨道的应力云图

由图7可知，车轮在光滑轨道上运行时，其振动加速度的幅值一直稳定在−0.2~0.2 m/s²的区间之内。车轮在有缺陷的轨道上运行时，在绝大部分的时间范围内，其振动加速度与光滑轨道的变化情况基本相同，但在2 s、5 s、8 s、9 s等时间点时加速度幅值突然增大到−0.4~0.4 m/s²，随后又减小到−0.2~0.2 m/s²区间。根据后处理的结果，在2 s、5 s、8 s、9 s时车轮刚好滚过轨道踏面的缺陷位置。由此可见，小车在无缺陷的轨道踏面上运行时，其振动加速度幅值维持在−0.2~0.2 m/s²范围之内；而当行驶过轨道踏面缺陷时，其振动加速度发生极为明显的突变，表现为振动加速度的幅值增大。

Figure 7. Acceleration-time diagram of the simulated trolley running on two types of tracks. (a) Smooth track; (b) Defective track; (c) Comparison between smooth track and defective track

图7. 模拟所得的小车在两种类型的轨道上运行的振动加速度-时间图。(a) 光滑的轨道；(b) 有缺陷的轨道；(c) 光滑轨道与有缺陷轨道的对比

根据RecurDyn软件对两种工况仿真的结果可知，可以通过小车在轨道上运行的振动加速度来判断轨道踏面的缺陷位置。小车行驶在无缺陷的轨道踏面时，其振动加速度在一个很小的范围内变化；当小车通过轨道踏面缺陷时，小车车轮与缺陷发生撞击，产生一个冲击荷载，该冲击荷载将会使得该位置的振动加速度发生突变。因此，如果采集的加速度信号的幅值在某些时间点产生明显的增大，而在大部分时间又处于较小的变化区间，则可以判断这些时间对应的轨道踏面位置存在缺陷。

4. 仿真结果与实验结果的对比

为了验证本文构建的仿真模型的可靠性，对广州港某轨道吊上小车轨道的振动加速度进行了现场测试，并将测试数据与仿真结果进行对比分析，如图8所示。结果表明，小车通过轨道时现场测试的加速度曲线图与RecurDyn软件仿真的结果非常接近。在现场测试的结果中，小车的加速度幅值基本保持在−0.3~0.3 m/s²之间，但是在2 s、5 s、8 s、9 s时加速度明显增大(−0.8~0.8 m/s²)，这些时间点对应于小车车轮通过轨道踏面缺陷的时刻。现场实验的结果表明，小车在轨道上行驶时振动加速度幅值突然增加的原因是车轮与轨道踏面缺陷发生作用。

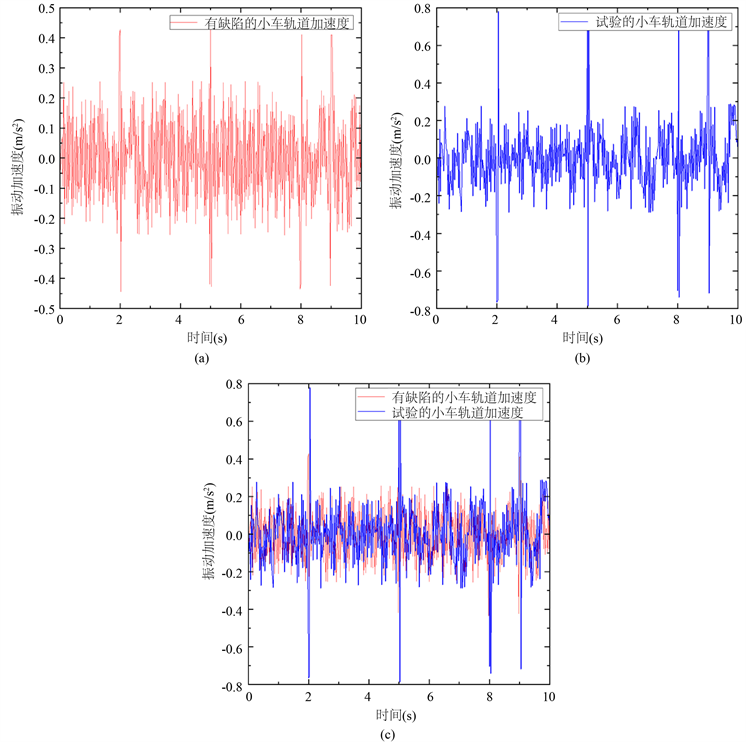
Figure 8. Vibration acceleration-time diagram of a trolley running on a defective track. (a) Simulated vibration acceleration-time diagram; (b) Vibration acceleration-time diagram measured in field test; (c) Comparison of two kinds of vibration acceleration-time diagram

图8. 小车在有缺陷轨道上运行的振动加速度–时间图。(a) 模拟的振动加速度-时间图；(b) 现场试验测得的振动加速度–时间图；(c) 两种振动加速度–时间对比图

5. 结论

本文以广州港某轨道吊为研究对象，基于RecurDyn软件对轨道踏面的典型工况进行了刚柔耦合多体动力学研究，获得了有缺陷工况和无缺陷工况下的加速度变化情况，得出结论如下：

1) 通过分析应力数据，可知模型的最大应力远小于材料的屈服极限；

2) 小车在无缺陷的轨道踏面行驶时，其振动加速度幅值维持在一个较小的区间；

3) 当小车通过有踏面缺陷的轨道时，小车车轮与踏面缺陷相撞而产生冲击荷载，导致该位置的振动加速度瞬间增大，而后减小到正常的加速度范围；

4) 通过对比仿真结果与现场测试结果，验证了仿真结果的可靠性。本文所提的方法为判断轨道踏面缺陷位置提供了理论依据，为小车轨道系统的日常维护和预警提供了数据支撑。

基金项目

湖南省自然科学基金项目(2019JJ50622)。

参考文献

NOTES

^*通讯作者。