多目标优化控制问题可行解的存在性

Existence of the Feasible Solutions for Multiobjective Optimal Control Problems

摘要: 本文主要考虑在欧式空间中，控制集合是一般可分度量空间的情况下，初始和终端状态满足等式和不等式约束的多目标优化控制问题。讨论其可行解的存在条件，并用不动点定理证明。

Abstract: In this paper, we are devoted to considering the existence of the feasible solutions for multiobjective optimal control problems on Euclidean space, where the endpoints satisfy some equality and inequality type constraints, and the control set is a separable metric space. And we prove it with the fixed point theorem.

1. 引言

令 $n,r,j,k\in \mathbb{N}$， $T>0$，U是度量空间。记 ${ℝ}^n$ 为n维欧式空间， $W^{1,1}\left(0,T;{ℝ}^n\right)$ 为从 $\left[0,T\right]$ 映到 ${ℝ}^n$ 的绝对连续函数集合， $\mathcal{U}$ 为从 $\left[0,T\right]$ 映到U的可测函数集合。给定映射 $f:\left[0,T\right]\times {ℝ}^n\times U\to {ℝ}^n$， ${\varphi }_0={\left({\varphi }_{-r},{\varphi }_{-r+1},\cdots ,{\varphi }_{-1}\right)}^{\text{T}}:{ℝ}^n\times {ℝ}^n\to {ℝ}^r$， $\varphi ={\left({\varphi }_{-r},{\varphi }_{-r+1},\cdots ,{\varphi }_{-1},{\varphi }_1,\cdots ,{\varphi }_j\right)}^{\text{T}}:{ℝ}^n\times {ℝ}^n\to {ℝ}^{r+j}$， $\psi :{ℝ}^n\times {ℝ}^n\to {ℝ}^k$，考虑如下控制系统：

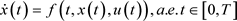(1)

其中 $u(\cdot )\in L^{\infty }\left(\left[0,T\right];{ℝ}^m\right)\cap \mathcal{U}$， $x(\cdot )\in W^{1,1}\left(\left[0,T\right],{ℝ}^n\right)$ 且满足端点约束

$\{\begin{array}{l}{\varphi }_i\left(x\left(0\right),x\left(T\right)\right)\le 0,i=1,\cdots ,j\\ \psi \left(x\left(0\right),x\left(T\right)\right)=0\end{array}$ (2)

对于上述系统，记 $\mathcal{P}$ 为所有可行解的集合，即 $\mathcal{P}=\left\{\left(x(\cdot ),u(\cdot )\right)\in \mathcal{U}\times W^{1,1}\left(0,T;{ℝ}^n\right)|\left(x(\cdot ),u(\cdot )\right)满足\left(1\right)\left(2\right)\right\}$，其中 $u(\cdot )$ 为可行控制， $x(\cdot )$ 为可行轨线。记 ${\mathcal{U}}_{ad}$ 为所有可行控制的集合。

与上述控制系统相关的优化控制问题：

(MCP) 最小化性能指标(目标函数)

$J\left(x(\cdot ),u(\cdot )\right)\triangleq {\varphi }_0\left(x\left(0\right),x\left(T\right)\right)$ (3)

当 $r=1$ 时，(MCP)为单目标优化控制问题，当 $r>1$ 时为多目标优化控制问题。生活中优化控制的数学模型大都是多目标优化控制问题，例如 [1] 中考虑的三位水平井设计优化问题就是两个目标的优化控制问题； [2] 中废水管理的数学模型所用到的优化控制问题有不止一个目标函数。力学和经济学领域也出现了多目标优化控制问题，为解决此类问题，研究多目标优化控制问题的优化条件是必要的，而在研究这些条件之前，我们必须保证解的存在性。

如今对于多目标优化控制问题的研究大部分对控制集合U是有凸性、闭性或其他要求的，例如 [3] [4] [5] [6] [7] [8] 及其中的参考文献。这就使得结论的适用性非常局限，因为生活中的数学问题大多没有这么好的条件。在本篇论文中，我们只需要U是可分度量空间，来研究这种情况下具有端点约束的多目标优化控制问题可行解的存在性。

此篇论文结构如下：第二部分为主要结论做准备，给出需要的假设、定义和引理；第三部分叙述主要结论；第四部分证明此结论。

2. 准备

首先我们给出定理需要的假设：

(C1) U是一个可分的度量空间；

(C2) 映射 $f\left(=f\left(t,x,u\right)\right):\left[0,T\right]\times {ℝ}^n\times U\to {ℝ}^n$ 关于t可测，关于x是 $C^1$ 的，关于u连续。映射 $\varphi \left(=\varphi \left(x_1,x_2\right)\right):{ℝ}^n\times {ℝ}^n\to {ℝ}^{r+j}$ 和 $\psi =\left(\psi \left(x_1,x_2\right)\right)={\left({\psi }_1,\cdots ,{\psi }_k\right)}^{\text{T}}:{ℝ}^n\times {ℝ}^n\to {ℝ}^k$ 是 $C^1$ 的。且存在常数 $K>0$，存在 $x_0\in {ℝ}^n$，s. t.

$\begin{array}{l}\left|f\left(t,x,u\right)-f\left(t,\hat{x},u\right)\right|\le K\left|x-\hat{x}\right|,\\ \left|\varphi \left(x_1,x_2\right)-\varphi \left({\hat{x}}_1,{\hat{x}}_2\right)\right|\le K\left(\left|x_1-{\hat{x}}_1\right|+\left|x_2-{\hat{x}}_2\right|\right),\\ \left|\psi \left(x_1,x_2\right)-\psi \left({\hat{x}}_1,{\hat{x}}_2\right)\right|\le K\left(\left|x_1-{\hat{x}}_1\right|+\left|x_2-{\hat{x}}_2\right|\right),\\ \left|f\left(t,x_0,u\right)\right|\le K\end{array}$

对于任意的 $\left(t,u\right)\in \left[0,T\right]\times U$，任意的 $x,\hat{x},x_1,x_2,{\hat{x}}_1,{\hat{x}}_2\in {ℝ}^n$ 均成立。

接下来给出一些定义和记号：

Definition 2.1：我们称可行解 $\left(\bar{x}(\cdot ),\bar{u}(\cdot )\right)\in \mathcal{P}$ 为(MCP)的弱有效最优解，如果不存在可行解 $\left(\bar{x}(\cdot ),\bar{u}(\cdot )\right)\in \mathcal{P}$，s.t. ${\varphi }_i\left(x\left(0\right),x\left(T\right)\right)<{\varphi }_i\left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right),i\in \left\{-r,\cdots ,-1\right\}$。

在这一部分里我们假设 $\left(\bar{x}(\cdot ),\bar{u}(\cdot )\right)$ 是(MCP)的弱有效最优解。为了方便，对于任意定义在 $\left[0,T\right]\times {ℝ}^n\times U$ 上的映射 $\phi$，我们记 $\phi \left[t\right]=\phi \left(t,\bar{x}\left(t\right),\bar{u}\left(t\right)\right),a.e.t\in \left[0,T\right]$。

关于 $\left(\bar{x}(\cdot ),\bar{u}(\cdot )\right)$，我们令 $I_{A0}=\left\{i\in 1,\cdots ,j|{\varphi }_i\left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)=0\right\}\cup \left\{-r,\cdots ,-1\right\}$， $I_N=\left\{1,\cdots ,j\right\}\backslash I_{A0}$。

接下来给出证明主要结论需要用到的引理。

Lemma 2.1：令集合 $F=\left\{{\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u,W}\left(T\right),\forall W\in {ℝ}^n,u\in \mathcal{U}\right\}$，

其中 $X_{u,W}(\cdot )$ 对于a.e. $t\in \left[0,T\right]$ 满足

$\{\begin{array}{l}{\stackrel{\dot{}}{X}}_{u,W}\left(t\right)={\nabla }_{x}f\left[t\right]X_{u,W}\left(t\right)+f\left(t,\bar{x}\left(t\right),u\left(t\right)\right)-f\left[t\right]\\ X_{u,W}\left(0\right)=W,\forall W\in {ℝ}^n\end{array}$， (4)

则F是凸集。

证明：令 $R\left(T\right)=\left\{X_{u,W}\left(T\right)|W\in {ℝ}^n,u(\cdot )\in \mathcal{U}\right\}$，显然我们只需要证明 $R\left(T\right)$ 是凸集。

对于 $\forall u_1(\cdot ),u_2(\cdot )\in \mathcal{U},W_1,W_2\in {ℝ}^n$， $\forall \alpha \in \left(0,1\right)$，下证 $\alpha X_{u_1,W_1}\left(T\right)+\left(1-\alpha \right)X_{u_2,W_2}\left(T\right)\in R$。

由(4)式， $X_{u_j,W_j}\left(T\right)=W_j+{\displaystyle {\int }_0^T\left({\nabla }_{x}f\left[s\right]X_{u_j,W_j}\left(s\right)+f\left(s,\bar{x}\left(s\right),u_j\left(s\right)\right)-f\left[s\right]\right)\text{d}s}$， $j=1,2$。

则 $\begin{array}{l}\alpha X_{u_1,W_1}\left(T\right)+\left(1-\alpha \right)X_{u_2,W_2}\left(T\right)\\ =\alpha W_1+\left(1-a\right)W_2+{\displaystyle {\int }_0^T\left({\nabla }_{x}f\left[s\right]X_{u_2,W_2}\left(s\right)+f\left(s,\bar{x}\left(s\right),u_2\left(s\right)\right)-f\left[s\right]\right)\text{d}s}\\ +\alpha {\displaystyle {\int }_0^T\left({\nabla }_{x}f\left[s\right]\left(X_{u_1,W_1}\left(s\right)-X_{u_2,W_2}\left(s\right)\right)+f\left(s,\bar{x}\left(s\right),u_1\left(s\right)-u_2\left(s\right)\right)\right)\text{d}s}\end{array}$

由Liapounoff定理， $\exists E\subseteq \left[0,T\right]$， $\left|E\right|=\alpha T$，s.t.

$\begin{array}{l}\alpha {\displaystyle {\int }_0^T\left({\nabla }_{x}f\left[s\right]\left(X_{u_1,W_1}\left(s\right)-X_{u_2,W_2}\left(s\right)\right)+f\left(s,\bar{x}\left(s\right),u_1\left(s\right)-u_2\left(s\right)\right)\right)\text{d}s}\\ ={\displaystyle {\int }_{\left[0,T\right]\cap E}\left({\nabla }_{x}f\left[s\right]\left(X_{u_1,W_1}\left(s\right)-X_{u_2,W_2}\left(s\right)\right)+f\left(s,\bar{x}\left(s\right),u_1\left(s\right)-u_2\left(s\right)\right)\right)\text{d}s}\end{array}$

令 $X_{u,W}\left(t\right)=\{\begin{array}{l}{X}_{u_1,W_1}\left(t\right),t\in E\\ X_{u_2,W_2}\left(t\right),t\in \left[0,T\right]\backslash E\end{array}$， $u\left(t\right)=\{\begin{array}{l}{u}_1\left(t\right),t\in E\\ u_2\left(t\right),t\in \left[0,T\right]\backslash E\end{array}$，

$\exists W=\alpha W_1+\left(1-a\right)W_2\in {ℝ}^n$，s.t.

$\alpha X_{u_1,W_1}\left(T\right)+\left(1-\alpha \right)X_{u_2,W_2}\left(T\right)=W+{\displaystyle {\int }_0^T\left({\nabla }_{x}f\left[s\right]X_{u,W}\left(s\right)+f\left(s,\bar{x}\left(s\right),u\left(s\right)\right)-f\left[s\right]\right)\text{d}s}\in R\left(T\right)$.

因此 $R\left(T\right)$ 是凸集，故F是凸集。证毕。

Lemma 2.2：若 $0\in IntF$，其中 $IntF$ 是集合F的内部，则 $\exists {\delta }_0>0$， $\exists \left(u_1(\cdot ),W_1\right),\cdots ,\left(u_{k+1}(\cdot ),W_{k+1}\right)\in \mathcal{U}\times {ℝ}^n$，s.t.

$B\left({\delta }_0\right)\subseteq co{\left\{{\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right\}}_{\eta =1}^{k+1}$，其中 $coA$ 记为集合A的凸包， $X_{u_{\eta },W_{\eta }}(\cdot )$ 是(4)式中 $\left(u,W\right)$ 替换为 $\left(u_{\eta },W_{\eta }\right)$ 的解。

证明：事实上，由 $0\in Int\left\{{\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u,W}\left(T\right)\right\}\subseteq {ℝ}^k$， $\exists \left(u_1(\cdot ),W_1\right),\cdots ,\left(u_{k+1}(\cdot ),W_{k+1}\right)\in \mathcal{U}\times {ℝ}^n$ 满足 $\left(u_2-u_1,W_2-W_1\right),\cdots ,\left(u_{k+1}-u_1,W_{k+1}-W_1\right)$ 线性无关，使得 $\exists {\delta }_0>0$，且 $B\left({\delta }_0\right)\subseteq co{\left\{{\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right\}}_{\eta =1}^{k+1}$。

Lemma 2.3：对于 $\epsilon >0$， $\exists E_{\epsilon }\subseteq \left[0,T\right]$，令 $u^{\epsilon }\left(t\right)=\{\begin{array}{c}u\left(t\right),t\in E_{\epsilon }\\ \bar{u}\left(t\right),t\notin E_{\epsilon }\end{array}$，相应的 $x^{\epsilon }\left(t\right)$ 满足

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}^{\epsilon }\left(t\right)=f\left(t,x^{\epsilon }\left(t\right),u^{\epsilon }\left(t\right)\right),a.e.t\in \left[0,T\right]\\ x^{\epsilon }\left(0\right)=\bar{x}\left(0\right)+\epsilon W\end{array}$， (5)

且 $\underset{\epsilon \to 0}{\lim }{x}^{\epsilon }\left(t\right)=\bar{x}\left(t\right)$。则 $x^{\epsilon }\left(t\right)-\bar{x}\left(t\right)=\epsilon X_{u,W}\left(t\right)+o\left(\epsilon \right)$。

证明：由(5)式， $x^{\epsilon }\left(t\right)=\bar{x}\left(0\right)+\epsilon W+{\displaystyle {\int }_0^{t}f\left(s,x^{\epsilon }\left(s\right),u^{\epsilon }\left(s\right)\right)\text{d}s}$，

由状态方程(1)， $\bar{x}\left(t\right)=\bar{x}\left(0\right)+{\displaystyle {\int }_0^{t}f\left[s\right]\text{d}s}$。记

$\begin{array}{c}{y}^{\epsilon }\left(t\right)=\frac{1}{\epsilon }\left(x^{\epsilon }\left(t\right)-\bar{x}\left(t\right)\right)\\ =\frac{1}{\epsilon }\left(\epsilon W+{\displaystyle {\int }_0^{t}f\left(s,x^{\epsilon }\left(s\right),u^{\epsilon }\left(s\right)\right)\text{d}s}-{\displaystyle {\int }_0^{t}f\left[s\right]\text{d}s}\right)\\ =W+\frac{1}{\epsilon }{\displaystyle {\int }_0^t\left(f\left(s,x^{\epsilon }\left(s\right),u^{\epsilon }\left(s\right)\right)-f\left(s,\bar{x}\left(s\right),u^{\epsilon }\left(s\right)\right)\right)\text{d}s}\\ +\frac{1}{\epsilon }{\displaystyle {\int }_0^t\left(f\left(s,\bar{x}\left(s\right),u^{\epsilon }\left(s\right)\right)-f\left[s\right]\right)\text{d}s}\\ =W+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^1\frac{\partial f\left(s,\bar{x}\left(s\right)+\tau \left(x^{\epsilon }\left(s\right)-\bar{x}\left(s\right)\right),u^{\epsilon }\left(s\right)\right)}{\partial x}{y}^{\epsilon }\left(s\right)\text{d}\tau \text{d}s}}\\ +{\displaystyle {\int }_0^t\left(f\left(s,\bar{x}\left(s\right),u\left(s\right)\right)-f\left[s\right]\right)\text{d}s}+\frac{1}{\epsilon }\gamma (\; t\; )\end{array}$

其中， $\Vert \gamma \left(t\right)\Vert \le {\epsilon }^2$。令 $\epsilon \to 0$，此时 $\underset{\epsilon \to 0}{\lim }{y}^{\epsilon }\left(t\right)=X_{u,W}\left(t\right)$。

故有 $x^{\epsilon }\left(t\right)-\bar{x}\left(t\right)=\epsilon X_{u,W}\left(t\right)+o\left(\epsilon \right)$。证毕。

3. 主要结论

这一部分中，我们给出可行控制的存在性定理，也就是本文主要结论。

Theorem 3.1： 假设(C1)-(C2)成立， $\left(\bar{x}(\cdot ),\bar{u}(\cdot )\right)$ 是(MCP)的弱有效最优解。若 $0\in IntF$，则一定能在 $\bar{u}(\cdot )$ 附近找到可行控制。即： $\forall \epsilon >0$， $\exists \delta >0$， $\exists u_{\epsilon }(\cdot )\in {\mathcal{U}}_{ad}$，满足 $d\left(\bar{u}(\cdot ),u_{\epsilon }(\cdot )\right)<\delta$，s. t. ${\Vert u_c^{\epsilon }(\cdot )-\bar{u}(\cdot )\Vert }_{L^{\infty }}<\epsilon$。

Remark 3.1： 可行控制的存在性即为可行解的存在性。

4. 证明主要结论

这一部分我们应用第二部分的几个引理和不动点定理证明Theorem 3.1。

Proof： Step 1. 对于 $\forall \alpha >0$， $\exists {\epsilon }_0>0$，s. t.对 $\forall \epsilon \in \left[0,{\epsilon }_0\right]$， $\exists E_{\epsilon }\subset \left[0,T\right]$ 满足 $\left|E_{\epsilon }\right|=\epsilon T$，使得下述性质成立：

(i)对于任意的 $\nu ={\left({\nu }_1,\cdots ,{\nu }_{k+1}\right)}^{\text{T}}$ 满足

${\nu }_{\eta }\ge 0$， $\eta =1\cdots ,k+1$ ； ${\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }}=1$ (6)

$\exists E_{\nu }^1,\cdots ,E_{\nu }^{k+1}\subset \left[0,T\right]$， $\exists L>0$ 使得

$\begin{array}{l}\left|E_{\nu }^{\eta }\right|={\nu }_{\eta }T,\\ {\displaystyle \underset{\eta =1}{\overset{k+1}{\cup }}{E}_{\nu }^{\eta }}=\left[0,T\right],\\ E_{\nu }^p\cap E_{\nu }^q=\varnothing ,\text{if}p\ne q,\\ {\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}H\left(E_{\nu }^{\eta },E_{\hat{\nu }}^{\eta }\right)}\le L\left|\nu -\hat{\nu }\right|\end{array}$ (7)

其中 $\hat{\nu }={\left({\hat{\nu }}_1,\cdots ,{\hat{\nu }}_{k+1}\right)}^{\text{T}}$ 满足(6)。

(ii) 令 $u_{\nu }^{\epsilon }\left(t\right)={\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{I}_{E_{\epsilon }\cap E_{\nu }^{\eta }}\left(t\right)u_{\eta }\left(t\right)}+I_{E_{\epsilon }^C}\left(t\right)\bar{u}\left(t\right)$，即 $u_{\nu }^{\epsilon }\left(t\right)=\{\begin{array}{l}{\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{I}_{E_{\nu }^{\eta }}\left(t\right)u_{\eta }\left(t\right),t\in E_{\epsilon }}\\ \bar{u}\left(t\right),t\notin E_{\epsilon }\end{array}$。记 $x_{\nu }^{\epsilon }(\cdot )$ 是以 $u_{\nu }^{\epsilon }(\cdot )$ 为控制，以 $\bar{x}\left(0\right)+\epsilon {\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }{W}_{\eta }}$ 为初值的轨线，则由Lemma 2.3，

$\left|x_{\nu }^{\epsilon }\left(t\right)-\bar{x}\left(t\right)-\epsilon X_{{\displaystyle \underset{\eta }{\sum }{\nu }_{\eta }{u}_{\eta }},{\displaystyle \underset{\eta }{\sum }{\nu }_{\eta }{W}_{\eta }}}\left(t\right)\right|<\frac{\alpha }{2}\epsilon$. (8)

与( [6] Lemma 4.5]中的证明相似，我们可以证明 $\left|X_{{\displaystyle \underset{\eta }{\sum }{\nu }_{\eta }{u}_{\eta }},{\displaystyle \underset{\eta }{\sum }{\nu }_{\eta }{W}_{\eta }}}\left(t\right)-{\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }{X}_{u_{\eta },W_{\eta }}\left(t\right)}\right|<\frac{\alpha }{2}$，则(8)式为

$\left|x_{\nu }^{\epsilon }\left(t\right)-\bar{x}\left(t\right)-\epsilon {\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }{X}_{u_{\eta },W_{\eta }}\left(t\right)}\right|<\alpha \epsilon$. (9)

Step 2. 对于给定的 $\alpha >0$，存在 ${\tilde{\epsilon }}_0\in \left(0,{\epsilon }_0\right]$，使得 $\forall \epsilon \in \left[0,{\tilde{\epsilon }}_0\right]$ 和 $\nu ={\left({\nu }_1,\cdots ,{\nu }_{k+1}\right)}^{\text{T}}$ 满足(6)式，有

$\left|\psi \left(x_{\nu }^{\epsilon }\left(0\right),x_{\nu }^{\epsilon }\left(T\right)\right)-\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)-\epsilon \left({\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right){\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }{W}_{\eta }}+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right){\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }{X}_{u_{\eta },W_{\eta }}\left(T\right)}\right)\right|\le \alpha \epsilon$.

证明过程与( [6] Lemma 4.5)相似。

Step 3. 由Lemma 2.2及上述证明过程，我们有

$\left|{\epsilon }^{-1}\left(\psi \left(x_{\nu }^{\epsilon }\left(0\right),x_{\nu }^{\epsilon }\left(T\right)\right)-\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)\right)-\left({\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right){\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }{W}_{\eta }}+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right){\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }{X}_{u_{\eta },W_{\eta }}\left(T\right)}\right)\right|\le {\delta }_0$

定义映射

$\begin{array}{l}\mathcal{F}:co{\left\{{\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right\}}_{\eta =1}^{k+1}\\ \to co{\left\{{\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right\}}_{\eta =1}^{k+1}\end{array}$

$\begin{array}{l}\mathcal{F}\left({\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }\left({\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right)}\right)\\ =-{\tilde{\epsilon }}_0{}^{-1}\left(\psi \left(x_{\nu }^{{\tilde{\epsilon }}_0}\left(0\right),x_{\nu }^{{\tilde{\epsilon }}_0}\left(T\right)\right)+{\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }\left({\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right)}\right)\end{array}$

由Brouwer不动点定理， $\exists {\nu }^0={\left({\nu }_0^1,\cdots ,{\nu }_0^{k+1}\right)}^{\text{T}}$ 满足(6)使得

$\begin{array}{l}\mathcal{F}\left({\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }^0\left({\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right)}\right)\\ =-{\tilde{\epsilon }}_0{}^{-1}\left(\psi \left(x_{{\nu }^0}^{{\tilde{\epsilon }}_0}\left(0\right),x_{{\nu }^0}^{{\tilde{\epsilon }}_0}\left(T\right)\right)+{\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }^0\left({\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}\left(T\right)\right)}\right)\\ ={\displaystyle \underset{\eta =1}{\overset{k+1}{\sum }}{\nu }_{\eta }^0({\nabla }_1\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W_{\eta }+{\nabla }_2\psi \left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u_{\eta },W_{\eta }}(\; T\; ))}\end{array}$

故有 $\psi \left(x_{{\nu }^0}^{{\tilde{\epsilon }}_0}\left(0\right),x_{{\nu }^0}^{{\tilde{\epsilon }}_0}\left(T\right)\right)=0$。

另一方面，当 $i\in I_N$ 时， ${\varphi }_i\left(x_{{\nu }_0}^{{\tilde{\epsilon }}_0}\left(0\right),x_{{\nu }_0}^{{\tilde{\epsilon }}_0}\left(T\right)\right)={\varphi }_i\left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)+O\left(\epsilon \right)<0$，

当 $i\in I_{A0}$ 时 ${\varphi }_i\left(x_{{\nu }_0}^{{\tilde{\epsilon }}_0}\left(0\right),x_{{\nu }_0}^{{\tilde{\epsilon }}_0}\left(T\right)\right)=\epsilon \left({\nabla }_1{\varphi }_i\left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)W+{\nabla }_2{\varphi }_i\left(\bar{x}\left(0\right),\bar{x}\left(T\right)\right)X_{u,W}\left(T\right)\right)+O\left({\epsilon }^2\right)<0$。

这就说明 $u_{{\nu }^0}^{{\tilde{\epsilon }}_0}(\cdot )\in {\mathcal{U}}_{ad}$。证毕。