1. 引言
基是研究向量空间和线性变换的一个非常重要和有用的工具。尤其在线性变换中,每一个线性变换完全取决于它在基上的作用。类似的,在研究置换群的过程中,基也是有用的工具。设G作用在集合
上,
的子集
被称为G的基,若满足
;换句话说,在群G中有且仅有单位元能稳定
中的所有元素。在Dixon的经典著作 [1] 中给出了基的一些相关命题。
有限本原群的研究已经有了一些成果,具体参见Cameron (1981) [2] 和Praeger (1990) [3]。对于极小基的研究,Burness在 [4] 中给出了点稳定子属于S-collection的有限典型群的base sizes,他对有限散在单群的base sizes也进行了讨论,具体参考 [5]。Fawcett,Praeger在 [6] 中给出了非本原线性群的base sizes。在 [7] 中,Libeck对本原置换群的base sizes进行讨论。而本文主要利用圈积构造一些传递置换群,确定它们在某种非本原作用下的极小基和base sizes。
2. 预备知识
本节主要给出一些本文中要用到的基本概念及结果。
定义2.1 [1] 非空集合
到自身的一个双射,称为
的一个置换。
中全体置换构成的群,称为
上的对称群,记作
。
定义2.2 [1] 设
是一个非空集合,其中的元素称为一个点,群G在
上的一个作用是指G到
上的一个同态,即:
1)
,
,其中1代表G中的单位元;
2)
,
,
。
定义2.3 [8] 设
为两个抽象群。
是同态映射,则N与F的半直积G为:
,
运算为
。
定义2.4 [8] 设G是群,H是有限集合
上的置换群
,设N是n个G的直积:
,对于任意
,映射
是N的一个自同构:
可作N与H的半直积
,叫做G和H的圈积,记作
。
.
定义2.5 [8] 群G作用在有限集合
上,
,
称为G在
上的逐点稳定子。若
,则称
为群G的基。若
是使得
成立的最小集合,则称
为群G的极小基。
3. 传递置换群在非本原作用下的极小基
定理3.1 设
,
对称群
与
的圈积
非本原作用在
个点上的极小基形如:
,
其中
为集合
中任意
个元素,
。
证明:令
,
,
,
,
设
,故
,群G在集合
的非本原作用如下:
下面考虑逐点稳定子
时,
中有哪些元素。
令
,
,
,
,则:
故
因为
,所以要使
,则K至少要稳定
个点,即
,故:
,
所以群
非本原作用在
上的极小基形如:
,
.
定理3.2:设
,当r为偶数时,二面体群
与对称群
的圈积
非本原作用在
个点上的极小基形如
,其中
,
。
当r为奇数时,极小基形如
,其中任意
,
。
证明:令
,
设
,则
。
群G在集合
上的作用同定理3.1,现在考虑逐点稳定子
时,
中有哪些元素。
首先考虑二面体群
的点稳定子群:
我们知道二面体群的点稳定子
,其中x为二阶元,下面考虑什么时候二面体群的点稳定子为1。
情况1:r为偶数时,
。
那么此时由二面体群的生成元可知当
时,
。所以当r为偶数时,使得逐点稳定子
的最小集合为:
,其中
。
即当r为偶数时,
非本原作用在
上极小基形如
,
。
例如:
当
时,
,二面体群
,如下图所示:
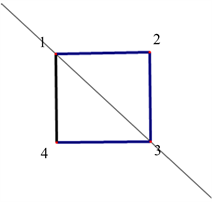
稳定点1,就要稳定点3,故
中稳定一个点的只有单位元与一个二阶元,即
,
,故有:
,
当
时,
,二面体群
,如下图所示:
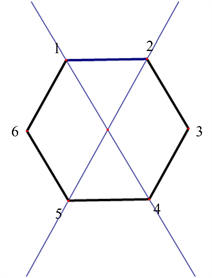
则有
,
,
,
,
情况2:当r为奇数时,二面体群:
此时稳定
中任意一个元素的也只有单位元与一个二阶元,故可知:
其中
,所以当r为奇数时,
非本原作用在
上极小基形如
,其中
,
。
定理3.3:设
,循环群
与对称群
的圈积
,非本原作用在
个点上的极小基形如
,其中任意
,
。
证明:令
,
,
G在集合
上的作用同以上两个定理,现在同样考虑逐点稳定子
时,
中有哪些元素。
因为
本原正则作用在
上,故任意
有
,则要使逐点稳定子
,需要稳定
这r个点,其中任意
。
故群
非本原作用在
上的极小基
,任意
,且
。