空间异性环境中Leslie-Gower捕食模型的稳定性与分支分析

doi:10.12677/PM.2022.121020

期刊菜单

空间异性环境中Leslie-Gower捕食模型的稳定性与分支分析
Stability and Bifurcation Analysis of the Leslie-Gower Predator-Prey Model in Spatial Heterogeneity Environment

DOI: 10.12677/PM.2022.121020, PDF, HTML, XML, 国家自然科学基金支持
作者: 雷梅娟, 张丽娜：西北师范大学数学与统计学院，甘肃兰州
关键词: 捕食模型；空间异性；局部分支；稳定性；Predator-Prey Model； Spatial Heterogeneity； Bifurcation； Stability

摘要: 本文考虑空间异性环境中修正的Leslie-Gower捕食模型。首先通过分析每个半平凡解相应特征值的符号，得到半平凡解的局部稳定性，其次利用局部分支理论证得分支解的存在性，最后经过讨论和证明，获得分支的方向以及分支解的稳定性。

Abstract: We concerned about the modified Leslie-Gower predator model in a spatially heterogeneous environment. Firstly, the local stability of the semi-trivial solution is obtained by analyzing the sign of the principal eigenvalue corresponding to each semi-trivial solution. Secondly, the existence of bifurcation solutions is proved by using the local branch theory. Finally, the direction of the branch and the stability of its solution are obtained after the discussion and proof.

文章引用：雷梅娟, 张丽娜. 空间异性环境中Leslie-Gower捕食模型的稳定性与分支分析[J]. 理论数学, 2022, 12(1): 157-164. https://doi.org/10.12677/PM.2022.121020

1. 引言

2003年，Aziz-Alaoui和Okiye对Leslie-Gower捕食模型作出了修正，考虑具有Holling-II型功能反应的模型 [1]

${\begin{cases} \frac{d u}{d t} = u (a_{1} - b_{1} u) - \frac{c u v}{1 + r_{1} u}, t > 0, \\ \frac{d v}{d t} = v (a_{2} - \frac{b_{2} v}{r_{2} + u}), t > 0, \end{cases}$ (1.1)

其中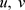分别表示食饵和捕食者的种群密度， $a_{1}, a_{2}$ 分别表示食饵和捕食者的内禀增长率， $b_{1}, b_{2}$ 分别表示食饵和捕食者的种内竞争系数，c表示食饵的种间相互作用系数， $r_{1}, r_{2}$ 为正常数， $r_{2} / b_{2}$ 表示食饵u严重匮乏时，环境对捕食者v的承载力。经无量纲化

$u = \frac{\bar{u}}{b_{1}}, v = \frac{\bar{v}}{b_{1} b_{2}}, γ = \frac{r_{1}}{b_{1}}, m = r_{2} b_{1}, β = \frac{c}{b_{1} b_{2}},$

并去掉“－”，系统(1.1)化为

${\begin{cases} \frac{d u}{d t} = u (a_{1} - u) - \frac{β u v}{1 + γ u}, t > 0, \\ \frac{d v}{d t} = v (a_{2} - \frac{v}{m + u}), t > 0, \end{cases}$ (1.2)

当 $γ = 0$ 时，显然模型有平凡平衡点 $(0, 0)$ ，半平凡平衡点 $(a_{1}, 0)$ 以及 $(0, m a_{2})$ 。当且仅当 $a_{1} > β m a_{2}$ ，模型(1.2)有唯一的正常数平衡点 $(\tilde{u}, \tilde{v})$ 。文献 [2] 对模型引入一般扩散后，对比了常微分系统与相应的扩散系统中非负平衡点的稳定性，发现它们的稳定性结论几乎完全相同，即非负平衡点的稳定性与扩散无关。具体地， $(0, 0)$ 和 $(a_{1}, 0)$ 是无条件不稳定的；当 $a_{1} \leq β m a_{2}$ 时， $(0, m a_{2})$ 是全局渐近稳定的；当 $a_{1} \geq β m a_{2}$ 时， $(\tilde{u}, \tilde{v})$ 是局部渐近稳定的。

文献 [2] 虽然引入了扩散，但仍假设所有系数都是常数，其中 $a_{1}, a_{2}$ 为常数在生物上表示物种处于均匀的空间环境，即空间同性，空间同性环境下扩散的捕食模型已经得到了广泛的研究 [3] [4] [5]，相对地，对于空间异性环境下扩散的捕食模型的研究还不够充分(这种空间异性环境在数学上可以通过将模型中部分系数取为变化的函数来表示)。在许多模型中，学者们已经发现空间异性环境下物种的动力学行为与空间同性下有显著不同。Choi等 [6] 研究发现非均匀坏境中，捕食者更有可能入侵成功；He等 [7] 研究表明，资源总量不变的情况下，空间异性环境中的物种会具有更大的竞争优势；Lou等 [8] 研究了空间异性环境下捕食模型的扩散效应，结果表明空间异性环境会激发出扩散对半平凡解稳定的影响。受以上文献的启发，我们把扩散和空间异性因素引入模型(1.2)，考虑下述模型

${\begin{cases} \frac{\partial u}{\partial t} = d_{1} Δ u + u (a_{1} (x) - u) - β u v, x \in Ω, t > 0, \\ \frac{\partial v}{\partial t} = d_{2} Δ v + v (a_{2} (x) - \frac{v}{m + u}), x \in Ω, t > 0, \\ \partial_{n} u = \partial_{n} v = 0, x \in \partial Ω, t > 0, \\ u (x, 0) = φ (x) \geq (\equiv) 0, v (x, 0) = ψ (x) \geq (\equiv) 0, x \in Ω, \end{cases}$ (1.3)

其中 $d_{1}, d_{2}$ 分别表示食饵和捕食者的扩散率， $Ω$ 是 $ℝ^{N} (N \geq 1)$ 中具有光滑边界 $\partial Ω$ 的有界区域， $n$ 是 $\partial Ω$ 上的单位外法向量， $\partial_{n} = \partial / \partial n$ ， $φ (x), ψ (x)$ 均为 $Ω$ 上的非负且不恒为零的光滑函数， $a_{1} (x), a_{2} (x)$ 在 $Ω$ 内为正且 $a_{1} (x), a_{2} (x) \in C^{r} (\bar{Ω}) (r \in (0, 1))$ 。

本文中，对于 $\bar{Ω}$ 上的连续函数 $f (x)$ ，记

$\overset{\lor}{f} = \min_{\bar{Ω}} f (x), \overset{\land}{f} = \max_{\bar{Ω}} f (x), \bar{f} = \frac{1}{| Ω |} \int f (x) d x .$

2. 预备知识与线性稳定性分析

下面我们介绍后续讨论所需的引理。先考虑单物种模型的平衡态问题

$d Δ u + u (m (x) - u) = 0, x \in Ω, \partial_{n} u = 0, x \in \partial Ω,$ (2.1)

其中 $m (x) \in C^{r} (\bar{Ω})$ ，且在 $\bar{Ω}$ 上不是常函数。由文献 [9] 知系统有唯一正解 $θ_{d, m}$ ，且 $\int_{Ω} m (x) d x < \int_{Ω} θ_{d, m} d x$ 。

引理1 [6] 由 $ℝ^{+}$ 到 $W^{2, p} (\bar{Ω}) \cap C^{2} (\bar{Ω})$ 的映射 $d \to θ_{d, m}$ 是连续的，此外，在 $\bar{Ω}$ 上

$\lim_{d \to 0} θ_{d, m} = \max m (x), \lim_{d \to \infty} θ_{d, m} = \bar{m} .$

讨论平凡解与半平凡解的稳定性时，涉及到特征值问题

$d Δ ψ + h (x) ψ + μ ψ = 0, x \in Ω, \partial_{n} ψ = 0, x \in \partial Ω$ (2.2)

其中d为正常数， $h \in L^{\infty} (Ω)$ ，记 $μ_{k} (d, h)$ 为第k个特征值。

引理2 [9] [10] (2.2)的主特征值 $μ_{1} (d, h)$ 关于d光滑，关于h连续且

1) 若 $\int_{Ω} h (x) d x \geq 0$ ，且 $h \neq 0$ ，则对任意 $d > 0$ 有 $μ_{1} (d, h) < 0$ ；

2) 若 $h_{1} (x) \leq h_{2} (x)$ ，则 $μ_{1} (d, h_{1}) \geq μ_{1} (d, h_{2})$ ，当且仅当 $h_{1} \equiv h_{2}$ 时等号成立；

3) $μ_{1} (d, h)$ 关于d严格单调递增，此外 $\lim_{d \to 0} μ_{1} (d, h) = \min_{\bar{Ω}} (- h)$ ， $\lim_{d \to \infty} μ_{1} (d, h) = - \bar{h}$ 。

为描述(2.1)的主特征值，我们引入不定权重的特征值问题

$Δ φ + λ h (x) φ = 0, x \in Ω, \partial_{n} φ = 0, x \in \partial Ω$ (2.3)

其中h不是常值函数且在 $Ω$ 内可以变号。若 $λ = λ_{1} (h)$ 时有正解，则 $λ_{1} (h)$ 是的主特征值。由文献 [7] 知，当 $\int_{Ω} h d x > 0$ 时， $λ_{1} (h) < 0$ ，当 $\int_{Ω} h d x < 0$ 时， $λ_{1} (h) > 0$ 。

(2.2)的主特征值 $μ_{1} (d, h)$ 与(2.3)的主特征值 $λ_{1} (h)$ 之间的关系由下述引理给出。

引理3 [9] [10] 若 $\int_{Ω} h d x < 0$ 且h在 $Ω$ 内变号，则当 $d < 1 / λ_{1} (h)$ 时， $μ_{1} (d, h) < 0$ ；当 $d = 1 / λ_{1} (h)$ 时， $μ_{1} (d, h) = 0$ ；当 $d > 1 / λ_{1} (h)$ 时， $μ_{1} (d, h) > 0$ 。

接下来，讨论半平凡平衡解的稳定性。显然，系统有平凡平衡解 $(0, 0)$ 和半平凡平衡解 $(θ_{d_{1}, a_{1}}, 0), (0, m θ_{d_{2}, a_{2}})$ 。

定理1 $(θ_{d_{1}, a_{1}}, 0)$ 是不稳定的。 $μ_{1} (d, a_{1} (x) - m β θ_{d_{2}, a_{2}}) > 0$ 时， $(0, m θ_{d_{2}, a_{2}})$ 是局部渐近稳定的； $μ_{1} (d, a_{1} (x) - m β θ_{d_{2}, a_{2}}) < 0$ 时， $(0, m θ_{d_{2}, a_{2}})$ 是不稳定的。若 $m β {\overset{\lor}{θ}}_{d_{2}, a_{2}} > {\overset{\land}{a}}_{1}$ ， $(0, m θ_{d_{2}, a_{2}})$ 是局部渐近稳定的；若 $m β {\bar{θ}}_{d_{2}, a_{2}} < {\bar{a}}_{1}$ ， $(0, m θ_{d_{2}, a_{2}})$ 是不稳定的；若 $m β {\bar{θ}}_{d_{2}, a_{2}} > {\bar{a}}_{1}$ ，且 $a_{1} (x) - m β θ_{d_{2}, a_{2}}$ 在 $Ω$ 内变号，则存在 $d_{1}^{*} = 1 / λ_{1} (a_{1} (x) - m β θ_{d_{2}, a_{2}})$ ，使得 $d_{1} < d_{1}^{*}$ 时， $(0, m θ_{d_{2}, a_{2}})$ 是不稳定的； $d_{1} > d_{1}^{*}$ 时， $(0, m θ_{d_{2}, a_{2}})$ 是局部渐近稳定的。

证明：记(1.3)在平衡解 $(u_{*}, v_{*})$ 的处线性化算子为 $L (u_{*}, v_{*})$ ，令 $- λ$ 是它的特征值，对应的特征函数为 $(ϕ, ψ)$ 。则 $(θ_{d_{1}, a_{1}}, 0)$ 的稳定性由特征值问题

${\begin{cases} d_{1} Δ ϕ + a_{1} (x) ϕ - 2 θ_{d_{1}, a_{1}} ϕ - β θ_{d_{1}, a_{1}} ψ + λ ϕ = 0, x \in Ω, \\ d_{2} Δ ψ + a_{2} (x) ψ + λ ψ = 0, x \in Ω, \\ \partial_{n} ϕ = \partial_{n} ψ = 0, x \in \partial Ω \end{cases}$ (2.4)

决定。若 $ψ \neq 0$ ，则 $λ$ 是算子 $- d_{2} Δ - a_{2} (x)$ 的特征值，因此 $λ = μ_{k} (d_{2}, a_{2} (x)) \geq μ_{1} (d_{2}, a_{2} (x))$ 。若 $ψ \equiv 0$ ，则 $λ$ 是算子 $- d_{1} Δ - a_{1} (x) + 2 θ_{d_{1}, a_{1}}$ 的特征值，因此 $λ = μ_{k} (d_{1}, a_{1} (x) - 2 θ_{d_{1}, a_{1}}) \geq μ_{1} (d_{1}, a_{1} (x) - 2 θ_{d_{1}, a_{1}})$ 。又因为 $θ_{d_{1}, a_{1}}$ 是 $d_{1} Δ θ_{d_{1}, a_{1}} + θ_{d_{1}, a_{1}} (a_{1} (x) - θ_{d_{1}, a_{1}}) = 0$ 的解，结合引理2知 $μ_{1} (d_{1}, a_{1} (x) - 2 θ_{d_{1}, a_{1}}) > μ_{1} (d_{1}, a_{1} (x) - θ_{d_{1}, a_{1}}) = 0$ ，用类似的方法得 $μ_{1} (d_{2}, a_{2} (x)) < μ_{1} (d_{2}, a_{2} (x) - θ_{d_{2}, a_{2}}) = 0$ ，因而

$λ \geq \min {μ_{1} (d_{1}, a_{1} (x) - 2 θ_{d_{1}, a_{1}}), μ_{1} (d_{2}, a_{2} (x))} = μ_{1} (d_{2}, a_{2} (x)) .$

设 $ψ_{1}$ 是主特征值 $μ_{1} (d_{2}, a_{2} (x))$ 对应的主特征函数，则特征值为 $μ_{1} (d_{2}, a_{2} (x))$ 时对应的特征函数是 $(ϕ_{1}, ψ_{1}) = (L_{1}^{- 1} (- β θ_{d_{1}, a_{1}} ψ_{1}), ψ_{1})$ ，其中 $L_{1} = - d_{1} Δ - a_{1} (x) + 2 θ_{d_{1}, a_{1}} - μ_{1} (d_{2}, a_{2} (x))$ ，因为 $L_{1}$ 的特征值都为正，所以 $L_{1}$ 可逆。也就是存在负特征值，因此平衡解 $(θ_{d_{1}, a_{1}}, 0)$ 不稳定。

同样 $(0, m θ_{d_{2}, a_{2}})$ 的稳定性由下面的特征值问题

${\begin{cases} d_{1} Δ ϕ + a_{1} (x) ϕ - m β θ_{d_{2}, a_{2}} ϕ + λ ϕ = 0, x \in Ω, \\ d_{2} Δ ψ + a_{2} (x) ψ - 2 θ_{d_{2}, a_{2}} ψ + θ_{d_{2}, a_{2}}^{2} ϕ + λ ψ = 0, x \in Ω, \\ \partial_{n} ϕ = \partial_{n} ψ = 0, x \in \partial Ω \end{cases}$ (2.5)

决定，若 $ϕ \equiv 0$ ，则 $λ$ 是算子 $- d_{2} Δ - a_{2} (x) + 2 θ_{d_{2}, a_{2}}$ 的特征值，因而

$λ = μ_{k} (d_{2}, a_{2} (x) - 2 θ_{d_{2}, a_{2}}) \geq μ_{1} (d_{2}, a_{2} (x) - θ_{d_{2}, a_{2}}) = 0.$

若 $ϕ \neq 0$ ，则 $λ$ 是算子 $- d_{1} Δ - a_{1} (x) + m β θ_{d_{2}, a_{2}}$ 的特征值，因此

$λ = μ_{k} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) \geq μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) .$

所以

$λ \geq \min {μ_{1} (d_{2}, a_{2} (x) - θ_{d_{2}, a_{2}}), μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}})} = \min {0, μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}})} .$

下面详细分析 $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}})$ 的符号. 由引理2知 $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}})$ 关于 $d_{1}$ 严格单调递增，且满足

$\lim_{d \to 0} μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) = \min_{\bar{Ω}} (m β θ_{d_{2}, a_{2}} - a_{1} (x)) \geq m β {\overset{\lor}{θ}}_{d_{2}, a_{2}} - {\overset{\land}{a}}_{1},$

$\lim_{d \to \infty} μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) = m β {\bar{θ}}_{d_{2}, a_{2}} - {\bar{a}}_{1},$

则如果 $m β {\bar{θ}}_{d_{2}, a_{2}} < {\bar{a}}_{1}$ ，那么 $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) < 0$ ；如果 $m β {\overset{\lor}{θ}}_{d_{2}, a_{2}} > {\overset{\land}{a}}_{1}$ ，那么 $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) > 0$ 。若 $m β {\bar{θ}}_{d_{2}, a_{2}} > {\bar{a}}_{1}$ 且 $a_{1} (x) - m β θ_{d_{2}, a_{2}}$ 在 $Ω$ 内变号，则由引理3知，存在 $d_{1}^{*} ≜ 1 / λ_{1} (a_{1} (x) - m β θ_{d_{2}, a_{2}})$ 使得当 $d < d_{1}^{*}$ 时， $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) < 0$ ；当 $d = d_{1}^{*}$ 时， $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) = 0$ ；当 $d > d_{1}^{*}$ 时， $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) > 0$ 。记 $(ϕ_{2}, ψ_{2})$ 是特征值 $μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) < 0$ 时对应的特征函数，则

$(ϕ_{2}, ψ_{2}) = (ϕ_{2}, L_{2}^{- 1} (θ_{d_{2}, a_{2}} ϕ_{2})),$

其中 $L_{2} = - d_{2} Δ - a_{2} (x) + 2 θ_{d_{2}, a_{2}} - μ_{1} (d_{1}, a_{1} (x) - m β θ_{d_{2}, a_{2}})$ 。易知 $L_{2}$ 可逆。从而 $(0, m θ_{d_{2}, a_{2}})$ 不稳定。用类似的方法可知 $(0, 0)$ 也不稳定。

注： $(0, 0)$ 不稳定表示引入u物种或v物种后，u，v物种至少有一个得以生存。 $(θ_{d_{1}, a_{1}}, 0)$ 不稳定表示v物种入侵系统成功。 $(0, m θ_{d_{2}, a_{2}})$ 不稳定表示u物种入侵系统成功， $(0, m θ_{d_{2}, a_{2}})$ 稳定表示u物种入侵系统不成功。

3. 半平凡解的局部分支

本节，我们以食饵的扩散率为分支参数，应用局部分支定理分析系统(1.3)半平凡平衡解的分支现象。注意到系统(1.3)的正平衡解满足下列方程

${\begin{cases} d_{1} Δ u + u (a_{1} (x) - u - β v) = 0, x \in Ω, \\ d_{2} Δ v + v (a_{2} (x) - \frac{v}{m + u}) = 0, x \in Ω, \\ \partial_{n} u = \partial_{n} v = 0, x \in \partial Ω . \end{cases}$ (3.1)

定义算子 $F (d_{1}, u, v) : ℝ^{+} \times X \to Y$

$F (d_{1}, u, v) = (\begin{matrix} d_{1} Δ u + u (a_{1} (x) - u - β v) \\ d_{2} Δ v + v (a_{2} (x) - \frac{v}{m + u}) \end{matrix}),$

其中

$X = {(u, v) \in W^{2, p} (Ω) \times W^{2, p} (Ω) : \partial_{n} u = \partial_{n} v = 0, x \in \partial Ω}, Y = L^{p} (Ω) \times L^{p} (Ω), p > N .$

对任意的 $d_{1} \in ℝ^{+}$ ，有 $F (d_{1}, 0, m θ_{d_{2}, a_{2}}) = 0$ ，通过计算，易得 $D_{d_{1}} F (d_{1}, u, v)$ ， $F_{u, v} (d_{1}, u, v)$ ， $D_{d_{1}} F_{u, v} (d_{1}, u, v)$ 存在且在 $(d_{1}, 0, m θ_{d_{2}, a_{2}})$ 的邻域内连续。

定理2 若 $m β {\bar{θ}}_{d_{2}, a_{2}} > {\bar{a}}_{1}$ 且 $a_{1} (x) - m β θ_{d_{2}, a_{2}}$ 在 $Ω$ 内变号，则当且仅当 $d_{1} = d_{1}^{*} ≜ 1 / λ_{1} (a_{1} (x) - m β θ_{d_{2}, a_{2}})$ 时，存在从半平凡解 $(0, m θ_{d_{2}, a_{2}})$ 分支出的解曲线。具体来说，存在 $δ > 0$ ，使在 $(d_{1}^{*}, 0, m θ_{d_{2}, a_{2}}) \in ℝ^{+} \times X$ 附近的正平衡解可表示为

${(d_{1}, u (s), v (s)) = (d_{1} (s), s ϕ_{*} + s^{2} u_{1} (s), m θ_{d_{2}, a_{2}} + s ψ_{*} + s^{2} v_{1} (s)) \in ℝ \times X : 0 < s < δ},$

且它是稳定的，其中 $d_{1} (0) = d_{1}^{*}$ ， $(ϕ_{*}, ψ_{*})$ 在证明中被定义， $(u_{1} (s), v_{1} (s))$ 是 $K e r F_{u, v} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}})$ 的补空间在X中关于s的有界光滑函数族。进一步地， $(d_{1}^{*}, 0, m θ_{d_{2}, a_{2}})$ 的分支方向由 ${d^{'}}_{1} < 0$ 刻画。

证明：首先，用局部分支定理证明分支解的存在性。设 $(ϕ, ψ) \in K e r F_{u, v} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}})$ ，则

${\begin{array}{l} d_{1}^{*} Δ ϕ + a_{1} (x) ϕ - m β θ_{d_{2}, a_{2}} ϕ = 0 \\ d_{2} Δ ψ + a_{2} (x) ψ - 2 θ_{d_{2}, a_{2}} ψ + θ_{d_{2}, a_{2}}^{2} ϕ = 0 \end{array}$ (3.2)

若 $ϕ \equiv 0$ ，则 $ψ$ 满足 $d_{2} Δ ψ + a_{2} (x) ψ - 2 θ_{d_{2}, a_{2}} ψ = 0$ ， $ψ \neq 0$ 时，0是 $- d_{2} Δ - a_{2} (x) + 2 θ_{d_{2}, a_{2}}$ 的特征值，故

$0 = μ_{k} (d_{2}, a_{2} (x) - 2 θ_{d_{2}, a_{2}}) \geq μ_{1} (d_{2}, a_{2} (x) - 2 θ_{d_{2}, a_{2}}) > μ_{1} (d_{2}, a_{2} (x) - θ_{d_{2}, a_{2}}),$

这与 $μ_{1} (d_{2}, a_{2} (x) - θ_{d_{2}, a_{2}}) = 0$ 产生矛盾，故 $ϕ \neq 0$ 。由第一个方程得 $μ_{1} (d_{1}^{*}, a_{1} (x) - m β θ_{d_{2}, a_{2}}) = 0$ ，设它对应的主特征函数为 $ϕ_{*}$ ，此时 $ψ$ 满足 $K ψ = θ_{d_{2}, a_{2}}^{2} ϕ_{*}$ ，其中 $K = - d_{2} Δ - a_{2} (x) + 2 θ_{d_{2}, a_{2}}$ ，易知K可逆，则 $ψ = K^{- 1} (θ_{d_{2}, a_{2}}^{2} ϕ_{*}) ≜ ψ_{*}$ 。因此，

$K e r F_{u, v} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}}) = s p a n {(\begin{matrix} ϕ_{*} \\ ψ_{*} \end{matrix})} .$

与上述方法类似，考虑它的共轭算子 $F_{u, v}^{*} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}})$ ，易得

$K e r F_{u, v}^{*} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}}) = s p a n {(\begin{matrix} ϕ_{*} \\ 0 \end{matrix})} .$

由Fredholm二择一定理知

$R a n g e F_{u, v} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}}) = {[K e r F_{u, v}^{*} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}})]}^{⊥} .$

因此， $c o d i m R a n g e F_{u, v} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}}) = 1$ ，又因为

$〈 D_{d_{1}} F (d_{1}, u, v) (\begin{matrix} ϕ_{*} \\ ψ_{*} \end{matrix}), (\begin{matrix} ϕ_{*} \\ 0 \end{matrix}) 〉 = - \int_{Ω} {| \nabla ϕ_{*} |}^{2} d x \neq 0,$

所以 $D_{d_{1}} F (d_{1}, u, v) (ϕ_{*}, ψ_{*}) \in R a n g e F_{u, v} (d_{1}^{*}, 0, m θ_{d_{2}, a_{2}})$ 。根据局部分支理论，系统在 $(d_{1}, 0, m θ_{d_{2}, a_{2}})$ 处存在半平凡解曲线 $(d_{1}, u (s), v (s))$ ，其中 $d_{1} = d_{1} (s)$ ， $u (s) = s ϕ_{*} + s^{2} u_{1} (s)$ ， $v (s) = m θ_{d_{2}, a_{2}} + s ψ_{*} + s^{2} v_{1} (s)$ ， $u_{1} (s), v_{1} (s)$ 是关于s的光滑函数。

接下来讨论分支的方向。先将 $d_{1} (s), u (s), v (s)$ 代入(3.1)的第一个方程并两边同除以s，再对s求一次导并令 $s = 0$ ，最后两边同乘 $ϕ_{*}$ 并在 $Ω$ 上积分，经计算得

${d^{'}}_{1} (0) = \frac{- \int_{Ω} (1 + K^{- 1} β θ_{d_{2}, a_{2}}^{2}) ϕ_{*}^{3} d x}{\int_{Ω} {| \nabla ϕ_{*} |}^{2} d x} < 0,$

因此该分支为左向的跨临界分支。

最后证明局部分支解的稳定性。记 $(u (s), v (s))$ 处的线性化算子为 $Γ_{s}$ ，令它实部最大的特征值是 $- η$ ，相应的特征函数为 $(ϕ, ψ)$ 。 $Γ_{0}$ 为 $(0, m θ_{d_{2}, a_{2}})$ 处的线性化算子，易知它有简单特征根0，对应的特征函数为 $(ϕ_{*}, ψ_{*})$ 。下面引入 $Γ_{s}$ 的扰动算子 $Γ_{d_{1}}$ ，

$Γ_{d_{1}} = (\begin{matrix} d_{1} Δ + a_{1} (x) - m β θ_{d_{2}, a_{2}} & 0 \\ θ_{d_{2}, a_{2}}^{2} & d_{2} Δ + a_{2} (x) - 2 θ_{d_{2}, a_{2}} \end{matrix})$

记 $Γ_{d_{1}}$ 的特征值为 $- γ$ ，相应的特征函数为 $(ϕ, ψ)$ ，则当 $| d_{1} - d_{1}^{*} | ≪ 1$ 时， $- γ$ 也是 $Γ_{d_{1}}$ 的简单特征值，且 $d_{1} \to d_{1}^{*}$ ， $γ \to 0$ ， $ϕ \to ϕ_{*}$ ， $ψ \to ψ_{*}$ 。由于

${\begin{array}{l} d_{1} Δ ϕ + a_{1} (x) ϕ - m β θ_{d_{2}, a_{2}} ϕ + γ ϕ = 0 \\ d_{2} Δ ψ + a_{2} (x) ψ - 2 θ_{d_{2}, a_{2}} ψ + θ_{d_{2}, a_{2}}^{2} ϕ + γ ψ = 0 \end{array}$ (3.3)

对(3.3)第一个方程两边同乘 $ϕ$ 且在 $Ω$ 上积分，经过简单计算得

$γ^{'} (d_{1}) = \frac{\int_{Ω} {| \nabla ϕ |}^{2} d x}{\int_{Ω} ϕ^{2} d x} > 0.$

因为 $Γ_{s}$ 的特征值 $- η$ 与 $Γ_{d_{1}}$ 的特征值 $- γ$ 之间存在

$\lim_{s \to 0} \frac{s d^{'} (s) γ^{'} (d_{1})}{η (s)} = - 1$

关系，所以当 $s \in (0, δ)$ 时， $η (s) < 0$ ，因而局部分支解 $(u (s), v (s))$ 是稳定的。

基金项目

国家自然科学基金(批准号：11761063)。

参考文献

[1]	Aziz-Alaoui, M.A. and Daher Okiye, M. (2003) Boundedness and Global Stability for a Predator-Prey Model with Modified Leslie-Gower and Holling-Type II Schemes. Applied Mathematics Letters, 7, 1069-1075. https://doi.org/10.1016/S0893-9659(03)90096-6
[2]	张丽娜, 吴守妍. 修正的Leslie-Gower捕食者-食饵扩散模型解的整体性态[J]. 山东大学学报(理学版), 2014, 49(1): 86-91.
[3]	Li, S.B. and Guo, S.J. (2020) Stability and Hopf Bifurcation in a Hutchinson Model. Applied Mathematics Letters, 101, 106066. https://doi.org/10.1016/j.aml.2019.106066
[4]	Guo, S.J. and Ma, L. (2016) Stability and Bifurcation in a Delayed Reaction-Diffusion Equation with Dirichlet Boundary Condition. Journal of Nonlinear Science, 26, 545-580. https://doi.org/10.1007/s00332-016-9285-x
[5]	Zou, R. and Guo, S.J. (2018) Dynamics in a Diffusive Preda-tor-Prey System with Ratio-Dependent Predator Influence. Computers Mathematics with Applications, 75, 1237-1258. https://doi.org/10.1016/j.camwa.2017.11.002
[6]	Choi, W. and Ahn, I. (2020) Predator-Prey Interaction Systems with Non-Uniform Dispersal in a Spatially Heterogeneous Environment. Journal of Mathematical Analysis and Appli-cations, 485, 123860. https://doi.org/10.1016/j.jmaa.2020.123860
[7]	He, X.Q. and Ni, W.M. (2013) The Effects of Diffusion and Spatial Variation in Lotka-Volterra Competition-Diffusion System II: Heterogeneity vs. Homogeneity. Journal of Dif-ferential Equations, 254, 528-546. https://doi.org/10.1016/j.jde.2012.08.032
[8]	Lou, Y. and Wang, B. (2017) Local Dynamics of a Diffusive Pred-ator-Prey Model in Spatially Heterogeneous Environment. Journal of Fixed Point Theory and Applications, 19, 755-772. https://doi.org/10.1007/s11784-016-0372-2
[9]	Cantrell, R. and Cosner, C. (2003) Spatial Ecology via Reaction-Diffusion Equations, John Wiley Sons, Ltd, Chichester. https://doi.org/10.1002/0470871296
[10]	Zou, R. and Guo, S.J. (2020) Dynamics of a Diffusive Leslie-Gower Predator-Prey Model in Spatially Heterogenous Envi-ronment. Discrete & Continuous Dynamical Systems B, 25, 4189-4210.

为你推荐

友情链接