1. 引言
剪力墙结构作为重要的高层建筑抗侧力结构体系,其抗震性能的研究一直以来都是一个热点方向。通过对剪力墙结构有限元模型进行研究,是分析与预测该结构实际破坏模式与承载能力的重要方式。关于剪力墙结构的数值模拟研究,通常会采用钢筋–混凝土分离式模型进行建模,但多数研究只是将钢筋直接嵌入混凝土中,不考虑钢筋和混凝土之间的粘结、滑移 [1],这与结构实际情况不符,会造成模型结果产生较大的误差。
本文基于ABAQUS有限元分析软件建立剪力墙模型,通过钢筋屈服强度的退化来反映钢筋–混凝土界面粘结滑移和混凝土保护层剥落等引起的综合退化效果 [2],并结合剪力墙拟静力抗震试验结果,对比分析验证了该模型的可靠性。
2. 剪力墙模型概况
2.1. 试件尺寸
为能直观的对比分析模型的准确性,数值模型的建立与剪力墙抗震试验试件的设计一致,试件尺寸及配筋如图1所示。试件截面形式为一字形,试验墙体为一级剪力墙,墙肢截面厚度为160 mm,截面长度为1300 mm,试验试件墙体高度为2400 mm,计算高度为2550 mm。基本尺寸为1300 mm × 160 mm × 2400 mm,墙体采用C25混凝土,试件配筋均为HRB400级钢筋,分布筋采用双排,竖向与水平分布筋均为Φ8@200,试件两端为构造边缘构件,配置6根Φ14竖向钢筋和Φ8@100的箍筋。设计轴压比0.2,竖向荷载412 KN。
2.2. 试验现象与破坏模式
剪力墙试件在循环往复荷载作用下表现为压弯破坏,剪力墙体最终的破坏形式为角部受压区混凝土被压碎、钢筋屈服,同时伴有大量的弯曲和弯剪斜裂缝。墙体破坏模式见图2。

Figure 1. Specimen size and reinforcement drawing
图1. 试件尺寸及配筋图

Figure 2. Final failure state of test piece
图2. 试件最终破坏状态
3. 有限元模型
3.1. 混凝土本构模型
混凝土本构关系采用《混凝土结构设计规范》 [3] (GB 50010-2010),如图3所示,单轴受拉时:

Figure 3. Uniaxial stress-strain curve of concrete
图3. 混凝土单轴应力–应变曲线
单轴受压时:
3.2. 钢筋本构模型
采用下式定义的强度退化模型考虑累积损伤引起的钢筋混凝土构件的受弯承载力退化。
其中
为第i个循环的有效累计滞回耗能;
为第i个循环的滞回耗能;
为屈服后刚度系数;
为第i个循环达到的峰值应变;
为构件在单调荷载加载下破坏时的钢筋受拉应变。图4中
为第i个加载循环的屈服强度,正号为正向加载,负号则为反向加载。
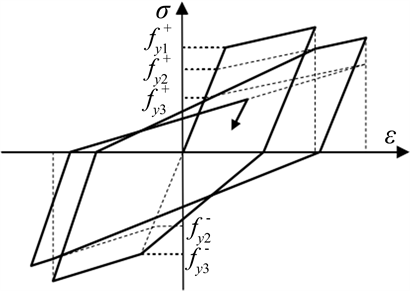
Figure 4. Reinforcement strength degradation model
图4. 钢筋退化模型
3.3. 混凝土损伤准则
本文的混凝土损伤准测采用ABAQUS的CDP模型(混凝土损伤塑形模型)。该模型基于Lubliner [4] 和Lee [5] 提出的塑形损伤模型,通过各项同性拉伸、压缩以及各项同性弹性的损伤理论来模拟混凝土中的非弹性行为,特别适用于模拟承受单调、循环荷载作用下的钢筋–混凝土模型。其弹性模量E通过损伤因子d和初始弹性模量
共同表达,公式如下 [6]:
其中,
为混凝土受压或受压应力,
为对应混凝土受压应变或受拉应变。根据选用的本构关系,即可求得混凝土损伤。
3.4. 模型设置
混凝土采用C3D8R单元,钢筋采用T3D2单元,纵筋和箍筋形成的钢筋网通过embedded region (内置区域)嵌入混凝土模型中,整体模型设置见图5。边界条件设置如下:
Initial:通过设置地梁及顶梁的中心参考点RP1、RP3并分别与地梁、顶梁表明耦合(Coupling),从而避免出现应力集中的现象。限制地梁参考点RP3的X、Y、Z三个方向的位移及转动,对于RP1,限制其垂直于剪力墙身方向的位移及剪力墙平面外的转动。
Step1:构件轴压比为0.2,计算得出总轴力为412KN,施加在参考点RP1上。
Step2:首先建立幅值表Amp1,采用位移控制模拟低周往复循环荷载下的拟静力试验,并将沿剪力墙宽度方向位移幅值变化施加在参考点RP1上。
4. 结果分析
4.1. 受压损伤云图
试验加载位移小于9 mm时,墙体无明显裂缝;试验中初始受弯裂缝出现在位移为12.9 mm时,此时水平荷载约为132 KN,裂缝首先出现在加载端一侧距离墙体底部200 mm处。加载至19 mm时,观察到距离墙体底部300 mm至700 mm间出现多道水平裂缝,宽度较小且有向中上部发展的趋势;加载至32 mm时,裂缝发展已经完全且部分主裂缝可看到张开与闭合;加载至42 mm时,两侧混凝土出现较大竖向裂缝,作动器回拉时,靠水平加载端一侧的混凝土先压碎,此时达到水平荷载最大值304 KN,裂缝数量不再增加;最终加载至68 mm,试件底部严重破坏,钢筋外露,试验结束。从混凝土受压损伤云图6中可以看出,模型模拟的最终损伤结果与试验结果基本吻合。由于在ABAQUS中内置的混凝土损伤(CDP)模型和考虑钢筋屈服强度退化的综合作用,有限元分析出现的损伤模式与试验较为接近,但模型出现损伤的时间早于试验损伤,这也与试验观察损伤会略微滞后有关。有限元分析中的受压损伤集中在两侧塑性铰区,试验中也观察到两侧混凝土压碎,并伴有大量混凝土碎屑。受拉损伤发展至距墙体底部约2/3处,且随墙体高度增加损伤程度降低,试验中观察到裂缝主要集中在中下部,进一步验证了模型的可靠性。
 (a) 受压损伤
(a) 受压损伤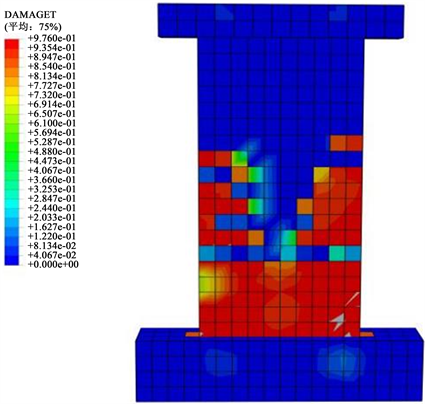 (b) 受拉损伤
(b) 受拉损伤
Figure 6. Concrete damage
图6. 混凝土损伤
4.2. 骨架曲线
将每次位移循环加载时的峰值点依次连接可得到骨架曲线,可以反映构件的强度、刚度、延性、耗能能力。循环往复加载的试验骨架曲线与模拟的骨架曲线大致接近,但极限荷载偏低。模拟曲线与试验曲线对比如图7所示。
由图可见,两曲线的走势相似。加载初期均为线弹性,钢筋未屈服,此时基本无塑性变形,但模拟曲线初始刚度更大。随着位移增大,骨架曲线逐渐由直线变为曲线,且随着位移增加,曲线的斜率逐渐变小,在40 mm左右达到峰值荷载(试验与模拟相差4.5%)。达到峰值荷载后,曲线逐渐放缓,承载力开始下降。可以明显看到,在设置了考虑综合退化效果的钢筋模型后,模拟曲线在达到峰值位移后承载力明显下降,并且与试验曲线吻合程度较好,水平荷载最大误差为7.36%。
4.3. 承载力分析
通过对骨架曲线的分析得到曲线的各特征点:屈服点、峰值点与极值点。对于没有明显拐点的骨架曲线确定屈服点,一般可采用破坏荷载法、双直线法、等能量法残余塑形法可近似确定,但当骨架曲线上有明显转折点时,可直接取该点作为屈服点。本文采用等能量法确定屈服点,即当构件实际吸收的能量与假定的弹塑性体吸收能量相等时 [7],对应的点即为屈服点。连接坐标原点与过骨架曲线最高点的水平直线做一条斜线,当斜线与骨架曲线相交的两块阴影面积相等时对应的点为屈服点。如图8所示:

Figure 8. Determination of yield point by equivalent elastoplastic principle
图8. 等能量法确定屈服点
计算公式如下:
其中,S为骨架曲线到达峰值点之前与坐标轴围成的面积;
为峰值荷载;
为对应峰值位移;
为所求屈服位移。
峰值荷载取水平荷载最大值,峰值位移取峰值荷载对应的位移。极限点取峰值荷载85%处的水平直线与滞回曲线下降段的交点,对应的位移即为极限位移。各特征点和对应位移值见表1。

Table 1. Numerical comparison of characteristic points between test and simulation
表1. 试验与模拟特征点数值对比
由表1可以看出,各特征点试验数据与模拟结果数值较为接近。数值模拟的屈服荷载与试验相差7.1%,屈服位移相差5.8%,峰值荷载相差7.3%,峰值位移相差4.5%,极限荷载与极限位移分别相差4.4%、4.9%。
表明有限元本构关系选取合理,模型基本可靠。
5. 结论
1) 引入钢筋屈服强度退化本构关系的有限元模型在损伤模式上与试验接近,有限元模型出现损伤的时间会略早于试验。受压损伤集中在两侧塑性铰区域,受拉损伤最高发展至距墙底2/3处。
2) 有限元模型与试验的骨架曲线走向相似,都经历了线弹性、弹塑性、破坏三个阶段,有限元模型中线弹性阶段的刚度更大且峰值荷载更大,但极限荷载略低于试验,体现出了更好的延性。
3) 通过等能量法得出屈服点,对试验各特征点进行分析,引入钢筋屈服强度退化本构关系的有限元模型与试验各特征点相差最大处出现在峰值点(7.9%),屈服点、极限点分别相差7.1%、4.9%。
综合损伤破坏模式、骨架曲线、特征点分析得出该模型与试验吻合良好,可用于对剪力墙的混凝土损伤及承载能力分析,具有一定工程价值。