Conformable分数阶单机无穷大电力系统的混沌容错同步

Tolerant Synchronization Analysis for Conformable Fractional Order Unipolar Infinite Power System

摘要: 基于反演设计和容错控制研究Conformable分数阶单机无穷大电力系统的混沌同步问题，在设计过程中引入虚拟的误差函数，利用李雅普诺夫稳定性理论确保带有执行器故障的被控系统的鲁棒同步，最后，模拟结果表明所提控制策略的有效性。

Abstract: A synchronization strategy based on backstepping design and tolerant control is studied for conformable fractional order unipolar infinite power system. The virtual control error functions are introduced in the design, and the Lyapunov stability theory is used to ensure the robust synchronization of the controlled systems with the actuator faults. Finally, the simulation results show the effectiveness of the proposed control strategy.

1. 引言

分数阶微积分是当前非线性研究领域的热点，能够较准确简洁地阐述具有历史记忆性和空间全域相关性等力学与物理过程，在量子力学、电磁振动、材料力学等领域有着十分广泛的应用 [1] [2] [3]。Khalil等 [4] 提出一种表现形式简洁易懂的Conformable分数阶微分定义，与整数阶微分有着良好分析、计算等统一 [5]，受到学者们的极大关注。Atangana等 [6] 继续发展了Conformable分数阶微分理论，为后继学者的研究奠定了基础。Feng和Meng [7] 根据Conformable分数阶微积分性质，研究了一类Conformable分数阶动力学方程的振荡和渐近性质。当前国内外关于Conformable分数阶微分的研究虽然有一些代表性成果 [7] [8] [9] [10] [11]，但尚处于初期阶段。

近年来，研究成果为数不多的容错控制已经成为一种有效的增加系统安全和可靠性的方法 [12] [13] [14] [15]，其设计方法一般有：被动方法、主动方法，即使故障发生，被控系统仍能保持渐近稳定。反演法 [16] [17] [18] [19] [20] 可将复杂的系统分解成不超过原系统阶数的子系统，通过设计中间虚拟控制量、修正虚拟控制律确保系统的稳定性，是一种性能优良的控制方法。Zhang等 [16] 设计反演控制器，对Morse吸引子做了混沌同步分析。Deng等 [17] 通过引入辅助信号，引入基于期望轨迹的前馈补偿概念，提出了一种实用的输出反馈反演控制器，用于液压执行器的运动控制。Zhang等 [19] 针对磁浮列车系统的稳定悬浮控制问题，设计了基于反步法的非线性控制器。Su等 [20] 在控制设计中引入虚拟控制函数，使用改进的自适应定律估计外部扰动的未知边界，利用未知边界的更新值，为不确定的非线性系统合成一类连续自适应鲁棒状态反馈控制器。

有效对电力系统进行稳定分析、评估是保障电力系统安全稳定运行的前提，Zhang等 [21] 基于轨迹断面特征根研究了电力系统暂态稳定定量评估方法，Zhao等 [22] 考虑二次系统具有时滞，用新的Lyapunov-Krasovskii泛函构造函数和解析方法得到了稳定判据，Wang等 [23] 首先利用分岔图及相图对系统的基本动力学行为进行分析，然后借助递归型滑模控制方法为混沌电力系统设计励磁控制器并给出具体表达式。如今单机无穷大系统模式在现实中的应用较为关注，文献 [24] [25] [26] [27] [28] 采用多种控制方法对系统性能指标进行稳定性分析。Yan [29] 采用Lyapunov指数谱、分岔图和吸引子相图分析了Conformable分数阶单机无穷大电力系统的分岔和混沌现象。整数阶电力系统模型已经无法满足研究需要，分析Conformable分数阶单机无穷大电力系统混沌振荡产生的机理有着重要的理论和实际意义 [29] [30] [31] [32]。

本文基于容错控制理论，设计中间虚拟控制量，通过修正虚拟控制律，基于反演方法设计带有执行器故障的控制器，研讨Conformable分数阶单机无穷大电力系统混沌同步问题。

2. 基本理论

定义：函数 $x\left(t\right):\left[a,+\infty \right)\to R$ 的conformable分数阶导数为

$\frac{{\text{d}}^{q}x\left(t\right)}{\text{d}{t}^q}=\underset{\epsilon \to 0}{\lim }\frac{x\left(t+\epsilon t^{1-q}\right)-x\left(t\right)}{\epsilon },t>0,0<q\le 1,$

$\frac{{\text{d}}^{q}x\left(0\right)}{\text{d}{t}^q}=\underset{t\to 0^{+}}{\lim }\frac{{\text{d}}^{q}x\left(t\right)}{\text{d}{t}^q}.$

注：函数 $x\left(t\right)$ 可导，则有 $\frac{{\text{d}}^{q}x\left(t\right)}{\text{d}{t}^q}=x^{\prime }\left(t\right)t^{1-q}$。

定理1：若 $\frac{{\text{d}}^{q}x\left(t\right)}{\text{d}{t}^q}=f\left(x\left(t\right)\right)$，则有 $x\left(t\right)=x\left(0\right)+{\displaystyle \underset{0}{\overset{t}{\int }}f\left(x\left(s\right)\right)s^{q-1}\text{d}s}$。

证明：

$\begin{array}{c}\frac{{\text{d}}^{q}x\left(t\right)}{\text{d}{t}^q}=\underset{\epsilon \to 0}{\lim }\frac{x\left(t+\epsilon t^{1-q}\right)-x\left(t\right)}{\epsilon }=\underset{\epsilon \to 0}{\lim }\frac{{\displaystyle \underset{0}{\overset{t+\epsilon t^{1-q}}{\int }}f\left(x\left(s\right)\right)s^{q-1}\text{d}s}-{\displaystyle \underset{0}{\overset{t}{\int }}f\left(x\left(s\right)\right)s^{q-1}\text{d}s}}{\epsilon }\\ =\underset{\epsilon \to 0}{\lim }\frac{{\displaystyle \underset{t}{\overset{t+\epsilon t^{1-q}}{\int }}f\left(x\left(s\right)\right)s^{q-1}\text{d}s}}{\epsilon }=\underset{\epsilon \to 0}{\lim }f\left(x\left(t+\epsilon t^{1-q}\right)\right){\left(t+\epsilon t^{1-q}\right)}^{q-1}{t}^{1-q}=f\left(x\left(t\right)\right).\end{array}$

所以有 $x\left(t\right)=x\left(0\right)+{\displaystyle \underset{0}{\overset{t}{\int }}f\left(x\left(s\right)\right)s^{q-1}\text{d}s}$ 成立。

定理2：设 $\frac{{\text{d}}^{q}x\left(t\right)}{\text{d}{t}^q}=f\left(x\left(t\right)\right)$，则 $\forall r>0$，有

$\frac{{\text{d}}^q}{\text{d}{t}^q}\Vert x\left(t\right)-y\left(t\right)\Vert \le \frac{{\left(x\left(t\right)-y\left(t\right)\right)}^{\text{T}}\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)}{{\Vert x\left(t\right)-y\left(t\right)\Vert }^2}\Vert x\left(t\right)-y\left(t\right)\Vert ,$

其中函数 $y\left(t\right)$ 满足 $\frac{{\text{d}}^{q}y\left(t\right)}{\text{d}{t}^q}=f\left(y\left(t\right)\right)$。

证明： $\forall r>0$， $\frac{{\text{d}}^q}{\text{d}{t}^q}\left({\text{e}}^{r\frac{t^q}{q}}x\left(t\right)\right)=r{\text{e}}^{r\frac{t^q}{q}}x\left(t\right)+{\text{e}}^{r\frac{t^q}{q}}f\left(x\left(t\right)\right)$。

于是有

$\frac{{\text{d}}^q}{\text{d}{t}^q}\left({\text{e}}^{r\frac{t^q}{q}}\left(x\left(t\right)-y\left(t\right)\right)\right)=r{\text{e}}^{r\frac{t^q}{q}}\left(x\left(t\right)-y\left(t\right)\right)+{\text{e}}^{r\frac{t^q}{q}}\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right).$

由定理1，得

${\text{e}}^{r\frac{t^q}{q}}\left(x\left(t\right)-y\left(t\right)\right)=\left(x\left(0\right)-y\left(0\right)\right)+{\displaystyle \underset{0}{\overset{t}{\int }}{\text{e}}^{r\frac{s^q}{q}}\left(r\left(x\left(s\right)-y\left(s\right)\right)+\left(f\left(x\left(s\right)\right)-f\left(y\left(s\right)\right)\right)\right)s^{q-1}\text{d}s.}$

${\text{e}}^{r\frac{t^q}{q}}\Vert x\left(t\right)-y\left(t\right)\Vert \le \Vert x\left(0\right)-y\left(0\right)\Vert +{\displaystyle \underset{0}{\overset{t}{\int }}{\text{e}}^{r\frac{s^q}{q}}{s}^{q-1}\Vert r\left(x\left(s\right)-y\left(s\right)\right)+\left(f\left(x\left(s\right)\right)-f\left(y\left(s\right)\right)\right)\Vert \text{d}s.}$

$r{\text{e}}^{r\frac{t^q}{q}}\Vert x\left(t\right)-y\left(t\right)\Vert +{\text{e}}^{r\frac{t^q}{q}}\frac{{\text{d}}^q}{\text{d}{t}^q}\Vert x\left(t\right)-y\left(t\right)\Vert \le {\text{e}}^{r\frac{t^q}{q}}\Vert r\left(x\left(t\right)-y\left(t\right)\right)+\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)\Vert .$

$\begin{array}{c}\frac{{\text{d}}^q}{\text{d}{t}^q}\Vert x\left(t\right)-y\left(t\right)\Vert \le \Vert r\left(x\left(t\right)-y\left(t\right)\right)+\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)\Vert -r\Vert x\left(t\right)-y\left(t\right)\Vert \\ =\frac{2r{\left(x\left(t\right)-y\left(t\right)\right)}^{\text{T}}\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)+\Vert f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\Vert }{\Vert r\left(x\left(t\right)-y\left(t\right)\right)+\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)\Vert +r\Vert x\left(t\right)-y\left(t\right)\Vert }.\end{array}$

由于 $\frac{2r{\left(x\left(t\right)-y\left(t\right)\right)}^{\text{T}}\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)+\Vert f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\Vert }{\Vert r\left(x\left(t\right)-y\left(t\right)\right)+\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)\Vert +r\Vert x\left(t\right)-y\left(t\right)\Vert }$ 关于 $r>0$ 单调递减，所以

$\begin{array}{c}\frac{{\text{d}}^q}{\text{d}{t}^q}\Vert x\left(t\right)-y\left(t\right)\Vert \le \underset{r\to +\infty }{\lim }\frac{2r{\left(x\left(t\right)-y\left(t\right)\right)}^{\text{T}}\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)+\Vert f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\Vert }{\Vert r\left(x\left(t\right)-y\left(t\right)\right)+\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)\Vert +r\Vert x\left(t\right)-y\left(t\right)\Vert }\\ =\frac{{\left(x\left(t\right)-y\left(t\right)\right)}^{\text{T}}\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)}{\Vert x\left(t\right)-y\left(t\right)\Vert }\\ =\frac{{\left(x\left(t\right)-y\left(t\right)\right)}^{\text{T}}\left(f\left(x\left(t\right)\right)-f\left(y\left(t\right)\right)\right)}{{\Vert x\left(t\right)-y\left(t\right)\Vert }^2}\Vert x\left(t\right)-y\left(t\right)\Vert .\end{array}$

3. 实例及数值仿真

带有执行器故障函数得Conformable分数阶单机无穷大电力系统混沌微分方程 [29] [30] 为驱动系统：

$\{\begin{array}{l}\frac{{\text{d}}^q{x}_1\left(t\right)}{\text{d}{t}^q}=x_2\left(t\right),\\ \frac{{\text{d}}^q{x}_2\left(t\right)}{\text{d}{t}^q}=-0.5x_2\left(t\right)+2.4x_3\left(t\right)+0.2-\sin x_1\left(t\right),\\ \frac{{\text{d}}^q{x}_3\left(t\right)}{\text{d}{t}^q}=x_4\left(t\right),\\ \frac{{\text{d}}^q{x}_4\left(t\right)}{\text{d}{t}^q}=-x_3\left(t\right)+m\left(t\right),\end{array}$ (1)

其中 $q=0.6$， $m\left(t\right)$ 是执行器故障函数。

响应系统为：

$\{\begin{array}{l}\frac{{\text{d}}^q{y}_1\left(t\right)}{\text{d}{t}^q}=y_2\left(t\right),\\ \frac{{\text{d}}^q{y}_2\left(t\right)}{\text{d}{t}^q}=-0.5y_2\left(t\right)+2.4y_3\left(t\right)+0.2-\sin y_1\left(t\right),\\ \frac{{\text{d}}^q{y}_3\left(t\right)}{\text{d}{t}^q}=y_4\left(t\right),\\ \frac{{\text{d}}^q{y}_4\left(t\right)}{\text{d}{t}^q}=-y_3\left(t\right)+\stackrel{⌢}{m}\left(t\right)-p\left(e_4\left(t\right)+k(e_3\left(t\right)+e_2\left(t\right)+e_1\left(t\right)\right),\end{array}$ (2)

其中 $\stackrel{⌢}{m}\left(t\right)$ 是 $m\left(t\right)$ 的估计。

设误差 $e_i\left(t\right)=y_i\left(t\right)-x_i\left(t\right),i=1,2,3,4$， $\tilde{m}\left(t\right)=\stackrel{⌢}{m}\left(t\right)-m\left(t\right)$，则有如下结论：

定理3：若执行器故障误差 $\tilde{m}\left(t\right)$ 是关于t的可导函数，满足

$\frac{{\text{d}}^q\tilde{m}\left(t\right)}{\text{d}{t}^q}=-\left(e_4\left(t\right)+k\left(e_3\left(t\right)+e_2\left(t\right)+e_1\left(t\right)\right)\right)-r\tilde{m}\left(t\right),$ (3)

当存在常数 $k>0,p>0,r>0$，满足

$W=\left(\begin{array}{ccc}-1& \frac{3}{4}& \frac{3}{4}\\ \frac{3}{4}& -1.9& \frac{1}{4}\\ \frac{3}{4}& \frac{1}{4}& -\left(k-2.4\right)\end{array}\right)<0$， $Q=\left(\begin{array}{ccccc}-1& \frac{3}{4}& \frac{3}{4}& \frac{3}{4}k& 0\\ \frac{3}{4}& -1.9& \frac{1}{4}& \frac{1-1.9k}{2}& 0\\ \frac{3}{4}& \frac{1}{4}& 2.4-k& \frac{2.4k-k^2}{2}& 0\\ \frac{3}{4}k& \frac{1-1.9k}{2}& \frac{2.4k-k^2}{2}& k-p& 0\\ 0& 0& 0& 0& -r\end{array}\right)<0$ (4)

时，驱动系统(1)和响应系统(2)混沌同步。

证明：由(1)和(2)得误差系统：

$\{\begin{array}{l}\frac{{\text{d}}^q{e}_1\left(t\right)}{\text{d}{t}^q}=e_2\left(t\right),\\ \frac{{\text{d}}^q{e}_2\left(t\right)}{\text{d}{t}^q}=-0.5e_2\left(t\right)+2.4e_3\left(t\right)-2\sin \frac{e_1\left(t\right)}{2}\cos \frac{x_1\left(t\right)+y_1\left(t\right)}{2},\\ \frac{{\text{d}}^q{e}_3\left(t\right)}{\text{d}{t}^q}=e_4\left(t\right),\\ \frac{{\text{d}}^q{e}_4\left(t\right)}{\text{d}{t}^q}=-e_3\left(t\right)+\tilde{m}\left(t\right)-p\left(e_4\left(t\right)+k\left(e_3\left(t\right)+e_2\left(t\right)+e_1\left(t\right)\right)\right),\end{array}$ (5)

由定理2和误差系统(5)中的第一个方程得：

$\frac{{\text{d}}^q\Vert e_1\left(t\right)\Vert }{\text{d}{t}^q}\le \frac{e_1\left(t\right)e_2\left(t\right)}{{\Vert e_1\left(t\right)\Vert }^2}\Vert e_1\left(t\right)\Vert .$

令 $e_2\left(t\right)=-e_1\left(t\right)$，则 $\frac{{\text{d}}^q\Vert e_1\left(t\right)\Vert }{\text{d}{t}^q}\le -\Vert e_1\left(t\right)\Vert$，

$\Vert e_1\left(t\right)\Vert \le \Vert e_1\left(0\right)\Vert {\text{e}}^{-\frac{t^q}{q}}\to 0,t\to +\infty .$

设 ${\alpha }_2\left(t\right)=e_2\left(t\right)+e_1\left(t\right)$，则结合(5)中第一、二个方程有

$\{\begin{array}{l}\frac{{\text{d}}^q{e}_1\left(t\right)}{\text{d}{t}^q}={\alpha }_2\left(t\right)-e_1\left(t\right),\\ \frac{{\text{d}}^q{\alpha }_2\left(t\right)}{\text{d}{t}^q}=0.5{\alpha }_2\left(t\right)-0.5e_1\left(t\right)+2.4e_3\left(t\right)-2\sin \frac{e_1\left(t\right)}{2}\cos \frac{x_1\left(t\right)+y_1\left(t\right)}{2}.\end{array}$

再次用定理2得：

$\frac{{\text{d}}^q\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert }{\text{d}{t}^q}\le \frac{-e_1^2\left(t\right)+1.5\left|e_1\left(t\right)\right|\left|{\alpha }_2\left(t\right)\right|+0.5{\alpha }_2^2\left(t\right)+2.4{\alpha }_2\left(t\right)e_3\left(t\right)}{{\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert }^2}\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert .$

令 $e_3\left(t\right)=-{\alpha }_2\left(t\right)$，则有

$\begin{array}{c}\frac{{\text{d}}^q\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert }{\text{d}{t}^q}\le \frac{-e_1^2\left(t\right)+1.5\left|e_1\left(t\right)\right|\left|{\alpha }_2\left(t\right)\right|-1.9{\alpha }_2^2\left(t\right)}{{\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert }^2}\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert \\ \le -0.25\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert .\end{array}$

于是有 $\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right)\right)\Vert \le \Vert \left(e_1\left(0\right),{\alpha }_2\left(0\right)\right)\Vert {\text{e}}^{-0.25\frac{t^q}{q}}\to 0$， $t\to +\infty$。

设 ${\alpha }_3\left(t\right)=e_3\left(t\right)+{\alpha }_2\left(t\right)$，则结合(5)中第一、二、三个方程有

$\{\begin{array}{l}\frac{{\text{d}}^q{e}_1\left(t\right)}{\text{d}{t}^q}={\alpha }_2\left(t\right)-e_1\left(t\right),\\ \frac{{\text{d}}^q{\alpha }_2\left(t\right)}{\text{d}{t}^q}=-1.9{\alpha }_2\left(t\right)-0.5e_1\left(t\right)+2.4{\alpha }_3\left(t\right)-2\sin \frac{e_1\left(t\right)}{2}\cos \frac{x_1\left(t\right)+y_1\left(t\right)}{2},\\ \frac{{\text{d}}^q{\alpha }_3\left(t\right)}{\text{d}{t}^q}=2.4{\alpha }_3\left(t\right)-1.9{\alpha }_2\left(t\right)-0.5e_1\left(t\right)-2\sin \frac{e_1\left(t\right)}{2}\cos \frac{x_1\left(t\right)+y_1\left(t\right)}{2}+e_4\left(t\right).\end{array}$

再次利用定理2得：

$\begin{array}{c}\frac{{\text{d}}^q\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert }{\text{d}{t}^q}\le [\frac{-e_1^2\left(t\right)+1.5\left|e_1\left(t\right)\right|\left|{\alpha }_2\left(t\right)\right|-1.9{\alpha }_2^2\left(t\right)+0.5{\alpha }_2\left(t\right){\alpha }_3\left(t\right)}{{\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert }^2}\\ +\frac{2.4{\alpha }_3^2\left(t\right)+1.5\left|e_1\left(t\right)\right|\left|{\alpha }_3\left(t\right)\right|+e_4\left(t\right){\alpha }_3\left(t\right)}{\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert }]\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert .\end{array}$

令 $e_4\left(t\right)=-k{\alpha }_3\left(t\right)$，则有

$\frac{{\text{d}}^q\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert }{\text{d}{t}^q}\le \frac{{\left(\begin{array}{c}\left|e_1\left(t\right)\right|\\ \left|{\alpha }_2\left(t\right)\right|\\ \left|{\alpha }_3\left(t\right)\right|\end{array}\right)}^{\text{T}}W\left(\begin{array}{c}\left|e_1\left(t\right)\right|\\ \left|{\alpha }_2\left(t\right)\right|\\ \left|{\alpha }_3\left(t\right)\right|\end{array}\right)}{{\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert }^2}\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert .$

由条件(4)中 $W<0$ 知， $\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right)\right)\Vert \to 0$， $t\to +\infty$。

设 ${\alpha }_4\left(t\right)=e_4\left(t\right)+k{\alpha }_3\left(t\right)$，则结合(5)中第一、二、三、四个方程有

$\{\begin{array}{l}\frac{{\text{d}}^q{e}_1\left(t\right)}{\text{d}{t}^q}={\alpha }_2\left(t\right)-e_1\left(t\right),\\ \frac{{\text{d}}^q{\alpha }_2\left(t\right)}{\text{d}{t}^q}=-1.9{\alpha }_2\left(t\right)-0.5e_1\left(t\right)+2.4{\alpha }_3\left(t\right)-2\sin \frac{e_1\left(t\right)}{2}\cos \frac{x_1\left(t\right)+y_1\left(t\right)}{2},\\ \frac{{\text{d}}^q{\alpha }_3\left(t\right)}{\text{d}{t}^q}=\left(2.4-k\right){\alpha }_3\left(t\right)-1.9{\alpha }_2\left(t\right)-0.5e_1\left(t\right)-2\sin \frac{e_1\left(t\right)}{2}\cos \frac{x_1\left(t\right)+y_1\left(t\right)}{2}+{\alpha }_4\left(t\right),\\ \frac{{\text{d}}^q{\alpha }_4\left(t\right)}{\text{d}{t}^q}=\left(k-p\right){\alpha }_4\left(t\right)+\left(2.4k-k^2-1\right){\alpha }_3\left(t\right)+\left(1-1.9k\right){\alpha }_2\left(t\right)-0.5k{e}_1\left(t\right)\\ -2k\sin \frac{e_1\left(t\right)}{2}\cos \frac{x_1\left(t\right)+y_1\left(t\right)}{2}+\tilde{m}\left(t\right).\end{array}$

再次利用定理2和(3)得：

$\begin{array}{l}\frac{{\text{d}}^q\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\alpha }_4\left(t\right),\tilde{m}\left(t\right)\right)\Vert }{\text{d}{t}^q}\\ \le \frac{Z^{\text{T}}\left(t\right)QZ\left(t\right)}{{\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\alpha }_4\left(t\right),\tilde{m}\left(t\right)\right)\Vert }^2}\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\alpha }_4\left(t\right),\tilde{m}\left(t\right)\right)\Vert ,\end{array}$

其中 $Z\left(t\right)={\left(\left|e_1\left(t\right)\right|,\left|{\alpha }_2\left(t\right)\right|,\left|{\alpha }_3\left(t\right)\right|,\left|{\alpha }_4\left(t\right)\right|,\left|\tilde{m}\left(t\right)\right|\right)}^{\text{T}}$。由条件(4)知，

$\Vert \left(e_1\left(t\right),{\alpha }_2\left(t\right),{\alpha }_3\left(t\right),{\alpha }_4\left(t\right),\tilde{m}\left(t\right)\right)\Vert \to 0,t\to +\infty .$

我们取 $k=4,r=3,p=200,m\left(t\right)=0.6+\sin \left(2x_4\left(t\right)\right)$，满足条件(4)，得到conformable分数阶单机无穷大电力系统(1)和(2)的混沌同步情况(见图1~4)。

Figure 1. Synchronization for state vectors $x_1\left(t\right),y_1(\; t\; )$

图1. 状态分量 $x_1\left(t\right),y_1\left(t\right)$ 同步

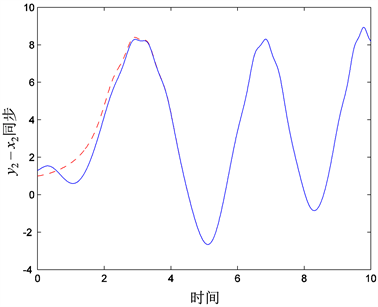
Figure 2. Synchronization for state vectors $x_2\left(t\right),y_2(\; t\; )$

图2. 状态分量 $x_2\left(t\right),y_2\left(t\right)$ 同步

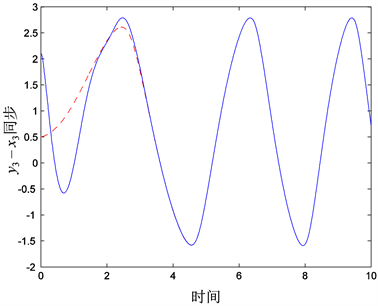
Figure 3. Synchronization for state vectors $x_3\left(t\right),y_3(\; t\; )$

图3. 状态分量 $x_3\left(t\right),y_3\left(t\right)$ 同步

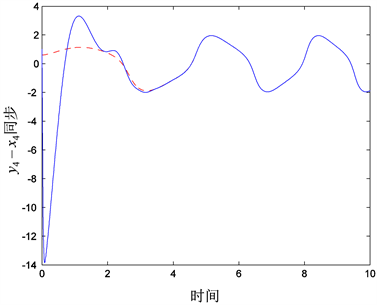
Figure 4. Synchronization for state vectors $x_4\left(t\right),y_4(\; t\; )$

图4. 状态分量 $x_4\left(t\right),y_4\left(t\right)$ 同步

注：当系统(1)、(2)中的第一二三个方程也存在执行器故障函数时，可模仿定理的推导得到类似结论。

4. 结论

本文基于容错控制、反演设计研究了Conformable分数阶单机无穷大电力系统的混沌同步问题。在故障存在的情况下，合理假设中间误差函数用反演法设计出控制器，仍能使系统具有渐近稳定性。

致谢

本文十分感谢山东省自然科学基金(项目编号：ZR2020QA002，ZR2017MA029)的资助。