1. 引言
成形力是辊弯成形中极为重要的一个参数,涉及到设备强度、工艺规程等诸多方面的问题。国内外对成形力的研究已经取得一定的进展,但是对于高强度刚的热辊弯成形力的研究尚属空白 [1] - [11]。本文以TC4钛合金型材为研究对象对其热辊弯成形力展开研究:沿用冷弯成形力内功与外功相等的原理,从屈服强度分布及变化情况入手在变形区内积分,得到热辊弯成形力的数学表达式。
钛合金由于其特殊的物理机械性能只能加热后实现塑性变形,而且热塑性变形的窗口很窄,对温度控制要求高。钛合金的热弯曲成形力的计算有两个特点:一是热变形是在很窄的温度窗口进行的,因此必须知道在这个窗口内材料的本构关系;二是折弯过程是伴随着板材的加热过程和冷却过程同时进行的,所以即使在这个窗口内,材料的本构关系也是连续变化的。由于现有的折弯力计算方法都是以冷弯为模型进行的,对于弹性模量和屈服强度连续变化的加热钛合金材料没有合适的折弯成形力计算方法。在计算之前为简化计算,提出几点假设 [1]:
1) 辊弯成形过程中型材为理想刚——塑性体。
2) 辊弯成形过程中,金属原板的横向弯曲沿着辊弯金属原板成形运动方向进行弯曲。
3) 角钢腿部的纵向弯曲忽略不计。
2. 钛合金连续热辊弯工艺
本文钛合金热弯成形力的研究依靠于特定的加工工艺及工况进行计算的如图1所示,本工艺采用火
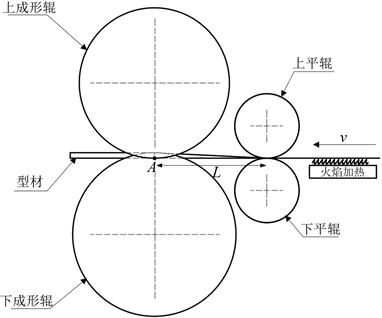
Figure 1. Profile hot roll bending principle diagram
图1. 型材热辊弯原理图
焰加热方式,钛合金板带匀速进入,首先经过火焰加热区温度逐渐升高,加热到指定温度,型材到达第一道次,即上、下平辊。平辊(第一机架)完成型材的平整和送进工作,此时型材开始降温,直至下一对成形辊即A点位置。其余机架承担一定的压弯成形任务使型材通过后被压成角型材,相邻两道次之间的距离为机架间距即L。
3. 变屈服强度成形力表达式
3.1. 最小变形区长度确定
连续式辊式成形机从第一架水平辊中心至最后一架辊轮中心的距离即为变形区长度,对于每一道次的变形区即相邻两机架之间的间距。确定变形区长度的原则是:必须保证带钢边缘在成形过程中不产生塑性变形,即型材边缘在折弯时的边缘纵向伸长量不应超过该种材料的弹性极限延伸量 [3]。本文主要以第一、第二道次为例进行成形力的计算。因第一个道次主要起到压紧、输送型材的目的,成形力为0。因此只需计算第二道次开始使型材弯曲时的成形力大小,也就只需确定第一、二个道次变形区长度即可。在两道次成形示意简图如图2所示,其中型材经第一道次的平整运输到第二道次,该型材在成形方向产生了纵向拉伸,型材原始长度为L,则拉伸后长度为L'。

Figure 2. Schematic diagram of profile forming for two adjacent passes (L-Length of deformation zone of this pass; L'-length of profile after extension; c-Critical bending angle of the pass; θ-bending angle of the pass; l-bending width)
图2. 相邻两道次型材成形示意简图(L-该道次变形区长度;L'-型材延伸后长度;c-该道次的临界弯曲角;θ-该道次弯曲角度;l-弯曲宽度)
为保证带钢边缘在成形过程中不产生塑性变形从而保证型材的加工质量(成形方向),那么型材边缘的延伸长度要小于该材料的弹性极限极限延伸量,依据该型材的弹性极限延伸量公式可以进而推导出最小变形区长度,机架间距应大于该变形区长度。该型材的弹性极限延伸量计算公式为:
(1)
式中:
——材料屈服强度;
E——材料的弹性模量;
最小变形区计算公式为:
(2)
式中:
——型材在当前道次弯曲角度;
l——该道次弯曲宽度;
根据式(2)可知,型材的弹性极限延伸量与该型材的屈服强度、弹性模量有关,而在钛合金热辊弯成形工艺中型材是逐步被加热到指定温度,因此在成形方向上该型材的屈服强度、弹性模量是呈线性分布的。型材的屈服强度变化与温度有对应关系,因此需确定每一时刻的温度变化情况由此确定该时刻型材屈服强度及弹性模量。如图2、图3所示,型材经O点开始加热,并加热至一定温度,随后脱离加热区开始降温,型材到达第一道次B点位置直至第二道次A点进行第一阶段的辊弯成形,该过程型材的温度是逐步降低的,而型材屈服强度是逐步升高的,期间每一个温度对应一个屈服强度值。因此需要知晓B、A两点的温度以获得型材经过对应B、A两点的屈服强度值。为计算简便,本文将B点至A点的温度曲线简化为线性,如图3所示:
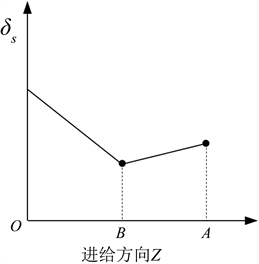
Figure 3. Schematic diagram of yield strength variation along the feed direction
图3. 屈服强度沿进给方向变化简图
由图3可列在变形区A-B内屈服应力变化的数学表达式:
(3)
型材变形主要发生在变形区长度上,而型材的纵向拉伸主要存在于边缘,因此需知晓变形区长度内边缘的平均温度及对应屈服强度、弹性模量值并带入式(1)、(2)求得在该工艺下的最小变形区长度。
3.2. 横向弯曲所需塑性功
由参考文献 [9] 得:对于矩形扁钢,当型材经过某一道次后角度变化为
时,在其弯曲方向上(扁钢宽度方向上)单位长度扁钢弯曲所消耗的塑性功为:
(4)
式中:
——材料屈服强度,在本工艺中在成形方向上存在变化;
s——型材厚度;
——在该成形道次型材的腿部弯曲角,理想情况下该角度随变形区长度L存在线性变化,
。
因弯曲变形主要发生在中心折弯区,为利于折弯,在钛合金加热时加热范围一般大于折弯区域,因此在整个折弯区域温度是一致的,不考虑横向屈服强度的变化,只考虑进给方向(成形方向)的屈服强度的变化,则式(4)为:
(5)
那么整个变形区由横向弯曲所需的塑性功为:
(6)
即将式(3)、(5)代入式(6):
(7)
3.3. 成形辊对型材所做的功
由文献 [9] 知当板材进入成型辊并稳定连续成型时,成型辊对板材的作用力在板材刚刚接触成型辊时为0 (入口处),在即将脱离成型辊而未脱离成型辊时最大(出口处),此作用力呈线性规律,命成型辊与板材接触的距离为
,出口处作用力为p,该道次增加的成型高度为
,那么距离入口处距离为z的作用力
与成型高度
表达式为 [5]:
(8)
(9)
因此在该道次成型辊对型材所做的功为:
(10)
3.4. 热弯成形力表达式建立
因为成型辊对型材作用力呈线性分布,那么成型辊对型材总作用力表达式为:
(11)
前文讲到型材达到规定截面形状横向弯曲所需塑性功等于成型辊对板材所做的功,因此
,则令式(7)式等于式(10)并带入式(11)并整理得热弯成形力为:
(12)
式中:
,其中
为型材腿部在该成形道次之前的总弯曲角。
那么最终整理得热弯成形力为:
(13)
式中:
——型材在该成形道次终辊位置折弯处屈服强度值;
——型材在进入该成形道次时(加热结束)待折弯处的屈服强度值;
l——角型材腿部长度。
4. 算例
试验具体的参数为:第一道次弯曲0˚,第二道次弯曲18˚,成形速度约为2 m/min,两机架间距为90 mm。上下成型辊的辊径直径尺寸均为140 mm,上、下平辊其辊径为60 mm,型材厚度约2 mm,宽度约为60 mm,腿长l = 30 mm。A点温度约为700摄氏度,其边缘平均温度约为550摄氏度,B点温度约为725摄氏度,边缘温度约为400摄氏度。
首先求出最小变形区长度,由试验得知型材在进入变形区进入降温过程时边缘的最高平均温度约为550摄氏度,为安全考虑取该温度下的屈服强度、弹性模量用作该道次最小变形区的计算参数。那么在该温度下TC4钛合金的屈服强度查阅文献 [12] [13] 知约为450 MPa,弹性模量E约为80 GPa,确定A、B两点屈服强度
、
,根据文献可知
,
,将以上参数带入(13)得成形力
。
4.1. 试验过程
现场试验在下成型辊的轴上连接一根长
钢管(IU段),并在钢管右端吊一重物(重物质量经测量可知),型材原始参数与上式一致。
本试验原理为:由成形力F产生的摩擦力作用于下成形辊圆心处的弯矩等于重物作用于该处的弯矩,那么当悬挂的重物恰好使成型辊稳定运行,则此重物的重量恰好使该弯矩等式成立,试验原理如图4所示:
由上图可以建立弯矩等式:
(14)
式中:f——由成型力产生的摩擦力,
,其中
为型材与成型辊之间的摩擦系数;
R——下成型辊直径,Rmm;
i——杠杆长度,
;
mg——重物的重力。
那么成型力计算公式为:
(15)
4.2. 试验与理论推导结果对比
试验测得结果为:当型材辊弯18˚、机架间距为90 mm、摩擦系数
、杠杆长度
、下成形辊半径
、悬挂重物重力约为105 N时恰好使成型辊匀速转动且型材匀速稳定成形。经公式(15)计算该参数下成形力大小F约为1002 N。公式所得结果与试验结果基本吻合,相对误差约17%,分析该钢管重量、人为操作为造成误差存在的原因。
5. 结论
1) 在现有冷弯成形力研究的基础上,确定了保证该型材成形质量的同时不存在纵向塑性变形确定最小变形区长度。依据所提出假设及相关文献建立了型材在辊弯过程中横向弯曲所需内功的数学表达式,从型材在加热过程中屈服强度在整个变形区内变化及分布情况入手利用积分法建立了变屈服强度下热弯成形力的数学表达式。
2) 通过现场多次实测,模拟前两个道次的成形情况测得实际热弯成型力与理论结果吻合良好,相对误差在20 以内。
基金项目
中央引导地方科技发展资金项目(206Z1008G)。
参考文献