WRF-CMAQ-BP神经网络空气质量预报模型研究

Study on Air Quality Forecast Model of WRF-CMAQ-BP Neural Network

摘要: 为减轻大气污染给人类带来的危害，国内外的学者在上个世纪就开始研究空气预报模型，高效且准确性高的预测模型可以预测未来若干天的大气污染情况，人们可以据此做出有效的应对措施以减少大气污染带来的危害。目前常用WRF-CMAQ模拟体系对空气质量进行预报，但由于受到各种不确定因素的影响，WRF-CMAQ预报模型的结果并不理想。本文主要工作是在WRF-CMAQ预报模型的基础上二次建模，提出了两个模型分别为WRF-CMAQ-BP和WRF-CMAQ-XGBoost模型，在构建网络后进行测试，在调参过程中发现WRF-CMAQ-BP模型的效果是更优的，因此本文用WRF-CMAQ-BP模型预测六种常规污染物的单日浓度值。

Abstract: In order to alleviate the harm brought about by atmospheric pollution, scholars at home and abroad began researching the air forecast model, high-efficiency and highly high prediction models can predict the future of atmospheric pollution in the next few days, people can make effective response measures to reduce the harm caused by atmospheric pollution. At present, the WRF-CMAQ simulation system is used to predict air quality, but the results of WRF-CMAQ forecasting model are not ideal due to the influence of various uncertain factors. This paper mainly works two models on the basis of the WRF-CMAQ forecast model, and two models are proposed to be WRF-CMAQ-BP and WRF-CMAQ-XGBOOST models, and test after building networks. During the adjustment process, it is found that the WRF-CMAQ-BP model is better, so the WRF-CMAQ-BP model is used to predict the single concentration value of six conventional pollutants.

1. 引言

建设生态文明是关系人民福祉、关系民族未来的大计，保护和建设好生态环境，实现可持续发展，是我国现代化建设中必须始终坚持的一项基本国策 [1]。由于我国仍处经济发展飞快的阶段，随着经济的增长，能源的消耗量也是巨大的，而由此产生的污染物对环境的影响也是令人担忧的，这可能极大危害人类的健康 [2]。环境污染又分为大气污染、水污染、土壤污染。其中影响最大的为大气污染，实践表明，精确的空气质量预测模型能够预测可能的污染过程并采取相应的措施应对，可以很大程度地减少大气污染及其对人类的伤害。

20世纪60年代以来，一些发达国家已经开始对空气质量预测技术进行了理论和应用的研究，后面形成了以高斯模型、拉格朗日模型或欧拉模型为理论基础的一系列的预测模型 [3]，近年来以数值模拟为基础，结合统计学习的集成模型也逐渐成为空气质量预测模型的热点。相对于国际而言，我国的空气预测模型发展得就比较晚了，直到20世纪90年代以后，我国才开始引进空气质量预测的概念，早期的统计预测模式探索了污染物与污染物、气象要素之间的相关性，随着技术的进步，要求不只要找到关联性，更要求能提前预测可能发生的污染过程并采取一定的有效措施。

目前常用的预报空气质量的模型为WRF-CMAQ模拟体系 [4] [5]，WRF是集数值天气预报、大气模拟、数据同化于一体的模型系统，主要用于大气环境模拟、天气研究、气象预报等，并为空气质量模型(CMAQ、CALPUFF、AERMOD、ADMS等)提供气象场。CMAQ模型是第三代空气质量模型系统，主要用于环境规划、环境保护标准、环境影响评价、环境监测与预报预警、环境质量变化趋势、总量控制、排污许可等有关政策的制定和编制，继而得到具体时间点或时间段的预报结果。虽然WRF-CMAQ模拟体系起到了较好的效果，但是由于存在一定的不确定性，预测结果的精确性有待进一步的研究。

随着人工智能和机器学习的发展，人工神经网络(ANNs)发展迅速，近年来和人工神经网络相关的空气质量预测模型的研究也逐步增多，Perez等人 [6] 开发了一种基于人工神经网络的统计预测模型，对PM₁₀浓度进行了预测，并在智利得到实证应用。

2. 模型假设及相关基础知识

2.1. 模型假设

一次预报数据中的“近地两米温度”等于实测数据中的“温度”；逐日实测数据中的缺失值可用同一天逐小时实测数据24小时的平均值填补。

2.2. 基础知识

首先给出空气质量指数(AQI)的计算公式，为了求解AQI的值，首先需要得到各项污染物的空气质量分指数(IAQI)，其计算公式为

$IAQ{I}_P=\frac{IAQ{I}_{Hi}-IAQ{I}_{Lo}}{B{P}_{Hi}-B{P}_{Lo}}\left(C_P-B{P}_{Lo}\right)+IAQ{I}_{Lo}$

其中 $IAQ{I}_P$ 表示污染物P的空气质量分指数，C_P表示污染物P的质量浓度值， $B{P}_{Hi},B{P}_{Lo}$ 分别表示与C_P相近的污染物浓度限值的高位值与低位值， $IAQ{I}_{Hi},IAQ{I}_{Lo}$ 分别表示与 $B{P}_{Hi},B{P}_{Lo}$ 对应的空气质量分指数。AQI取各分量指数中的最大值，在问题一中对于AQI的计算仅涉及六种污染物，所以AQI的计算公式为：

$AQI=\max \left\{IAQ{I}_{{\text{SO}}_{\text{2}}},IAQ{I}_{{\text{NO}}_{\text{2}}},IAQ{I}_{{\text{PM}}_{\text{10}}},IAQ{I}_{{\text{PM}}_{\text{2}\text{.5}}},IAQ{I}_{{\text{O}}_{\text{3}}},IAQ{I}_{\text{CO}}\right\}$

对于首要污染物的界定，给出如下的定义：

$首要污染物=\{\begin{array}{cc}无首要污染物,& AQI\le 50,\\ 首要污染物,& 50<AQI\le 100,IAQI最大的污染物\left(可多个\right),\\ 超标污染物,& AQI>100.\end{array}$

2.3. 模型建立

由于WRF-CMAQ预报模型的结果并不理想，本文提出了二次建模的概念，即在WRF-CMAQ预报模型的基础上结合实测数据进行二次建模以提高预报的准确性。充分利用附件1、2 (即监测点A、B、C的一次预报数据和实测数据)，建立一个同时适用于A、B、C三个监测点(监测点两两间直线距离 > 100 km，忽略相互影响)的二次预报数学模型是本文的目标，与此同时要求该模型能预测未来三天内六种污染物的单日浓度值并且预测结果中AQI预报值的最大相对误差应尽量小，且首要污染物预测准确度尽量高。在确保该二次预报数学模型高效性和准确性的基础上，使用该模型预测监测点A、B、C在2021年7月13日至7月15日六种常规污染物的单日浓度值，计算相应的AQI和首要污染物并以表格的形式呈现。

本文所涉及的数据处理和所有数值实验均在酷睿i5处理器2.40 GHz，内存4.00 GB配置的64位个人计算机，Matlab R2016a 的环境下进行。

2.4. 数据预处理

附件1、2¹中数据存在缺失或者不符合实际情况的问题，因此为了建立更加有效的二次预报数学模型，首先要对这些数据进行预处理，本节数据处理采用的方法仍为KNN插补法，但较之前不同的是，首先将这些数据转化为一个矩阵，以24小时的逐时测试数据为一组，具体的转化形式为，若选取连续三天的SO₂浓度为一个样本，则转化后的矩阵为3 × 24维大小的矩阵。以附件2中监测点B逐小时污染物浓度与气象实测数据中2019年4月16~18日SO₂ (ug/m³)浓度为例，转化后的矩阵为

$\Lambda =\left(\begin{array}{ccccccc}5& 5& 5& \cdots & 7& 6& 6\\ 7& 6& 6& \cdots & 5& 5& 6\\ 7& 7& 7& \cdots & 5& 6& 6\end{array}\right)$

其中 $\Lambda \in R^{3\times 24}$，若遇到数据缺失则赋值为“NAN”，然后利用KNNImputer对缺失值填补。

2.5. 建立基于WRF-CMAQ模型的BP神经网络的二次预报模型(WRF-CMAQ-BP)

首先将异常和缺失的数据进行了预处理，然后建立二次预报数学模型预测未来三天单日的污染物浓度值，由于WRF-CMAQ模型输出的一次预报数据为逐小时污染物浓度与气象数据，因此本小节将24小时逐时数据取平均值作为一个新的样本点。对于本文建立的两个二次预报数学模型，输入的一次预报数据和实际测试数据设置如下：

2.5.1. 输入一次预报数据和实测数据的选取

由于建立的二次预报模型要同时预测A、B、C三点的污染物浓度，所以在设置输入的数据集时充分考虑此因素，三个预测点的数据集都是整个数据集的1/3共选取了1272组数据。在建立模型前已经将气象条件和污染物的相关性进行分类，通过分类可知温度、湿度、气压、长波辐射和六种污染物的相关性比较强。因此对于输入层变量的选择可参考分类的结果。因此在选择一次预报数据的输入数据变量时，本文选取了近地两米温度、比湿、大气压、长波辐射和六种污染物作为输入层变量(共10个)。当通过网络训练完成后，用附件1、2中的实测数据集进行测试，实测数据集的选取方法类似于一次预报数据集的选取，三个预测点(A、B、C)各1/3共选取1272组数据，与一次预报数据不同的是，实测数据的变量为温度、湿度、气压、风速和六种污染物。

人工神经网络就是模拟人思维的第二种方式，这是一个非线性动力学系统，其特色在于信息的分布式存储和并行协同处理。虽然单个神经元的结构极其简单，功能也是有限的，但大量神经元构成的网络系统所能实现的行为却是极其丰富多彩的。如图1，BP (Back Propagation)神经网络 [7] [8] [9] 包含一个输入层，一个或多个隐含层，一个输出层，每层包含若干个节点。

Figure 1. BP neural network model

图1. BP神经网络模型

BP神经网络能学习和存贮大量的输入–输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络通过修正输出层和隐含层的权值，反复训练学习，使误差不断减小，从而得到满意的结果。接下来将给出基于WRF-CMAQ和BP神经网络的二次预报模型的算法流程图2及关键步骤的分析。

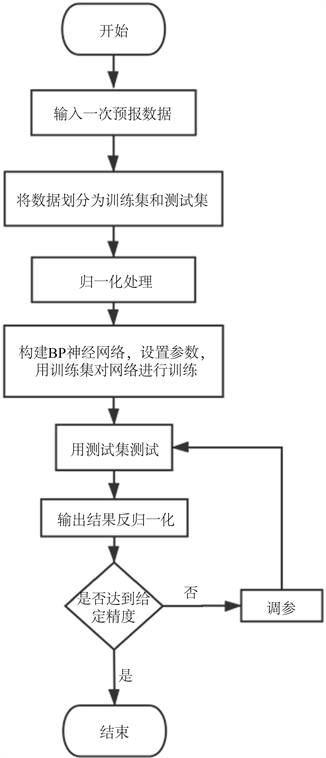
Figure 2. WRF-CMAQ-BP model flow chart

图2. WRF-CMAQ-BP模型流程图

2.5.2. 输入层神经元节点的选取

流程图2中输入元的个数对于要输出的预测结果非常重要，若节点数过少，可能会造成预测结果的精度不够，若节点数过多则会造成模型的计算量较大的同时也未必能提升结果的精确度。因此本文在数据集中选取了和污染物相关性较强的一些变量，流程图2中一次预报数据选取方法在上文中已详细介绍。

2.5.3. 训练集和测试集的划分

将输入的数据的80%用作训练集，20%用作测试集。

2.5.4. 调参(学习速率、训练次数、隐含层层数)

若流程图2中输出结果反归一化后仍未达到给定精度，则需要进行参数的调整，参数调整的标准是看平均绝对误差(MAE)是否足够的小，首先给出MAE的计算公式，对于样本 $X:=\left(x_1,x_2,x_3,\cdots ,x_n\right)$，

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left|x_j-{\hat{x}}_j\right|}$

其中 ${\hat{x}}_j$ 为预测值。下面将给出随着参数的变化，MAE的变化情况图：

图3(a)中横坐标是学习速率，纵坐标是MAE值，由图可知，当学习速率选择0.08时MAE的值是较低的，由图3(b)可得，隐含层节点数量选择9时MAE较小。

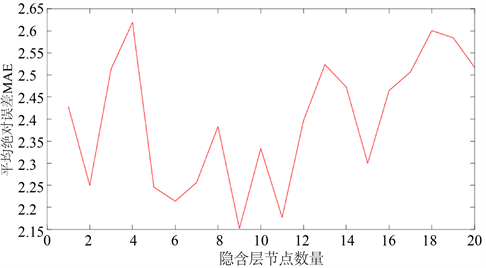(a)(b)

Figure 3. (a) Learning rate; (b) Implicit layer node number

图3. (a) 学习速率；(b) 隐含层节点数量

2.5.5. WRF-CMAQ-BP模型预测监测点A、B、C在2021年7月13日至7月15日 六种常规污染物的单日浓度值

WRF-CMAQ-BP模型最关键的点在于选取合适的输入层变量和调整参数，已在上文说明如何选取的，当训练集训练完成时，用测试集进行测试，下面将给出部分污染物的预测值和期望值的对比图：

图4中可以看出，选取了一千多个样本点，污染物SO₂，NO₂，PM₁₀，PM_2.5的预测值和期待值比较相近。下面将用WRF-CMAQ-BP模型预测监测点A、B、C在2021 年7月13日至7月15日六种常规污染物的单日浓度值及计算AQI值和首要污染物，具体见表1~3。

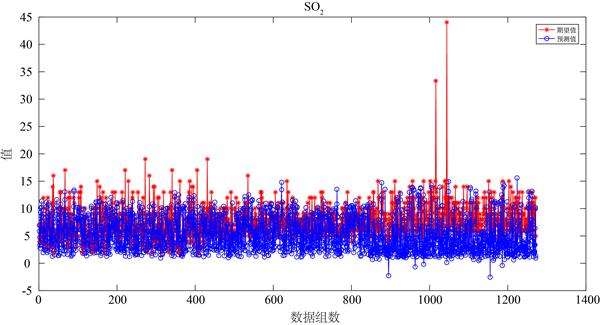(a) SO₂ 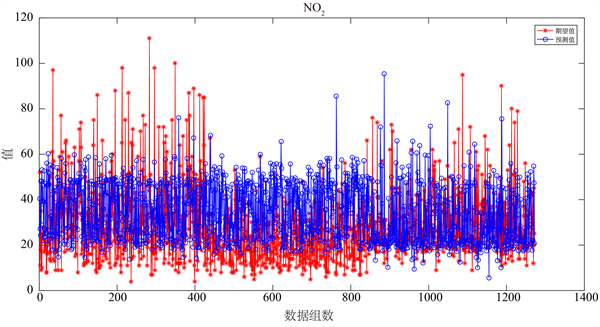(b) NO₂ 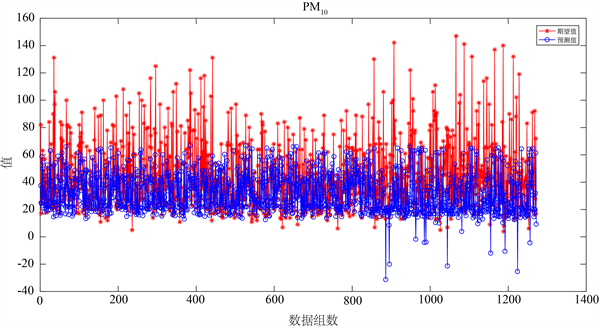(c) PM₁₀ 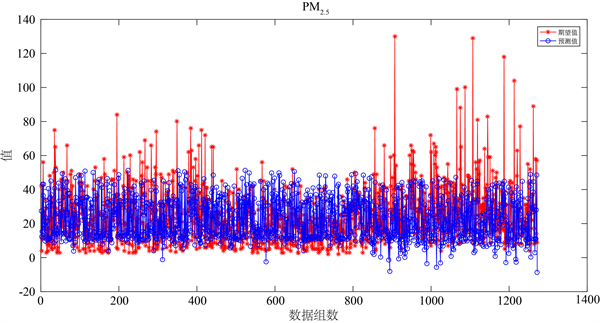(d) PM_2.5

Figure 4. Partial pollutant prediction renderings

图4. 部分污染物预测效果图

Table 1. WRF-CMAQ-BP model on pollutant concentration and AQI prediction results table (A)

表1. WRF-CMAQ-BP模型对污染物浓度及AQI预测结果表(A)

Table 2. WRF-CMAQ-BP model on pollutant concentration and AQI prediction results table (B)

表2. WRF-CMAQ-BP模型对污染物浓度及AQI预测结果表(B)

Table 3. WRF-CMAQ-BP model on pollutant concentration and AQI prediction results table (C)

表3. WRF-CMAQ-BP模型对污染物浓度及AQI预测结果表(C)

2.6. 建立基于WRF-CMAQ的XGBoost的二次预报模型(WRF-CMAQ-XGBoost)

虽然WRF-CMAQ-BP模型预报未来三天污染物浓度表现良好，但为了寻求更优的预报模型，本小节考虑将BP神经网络用XGBoost [10] [11] 替代。

XGBoost是2014年2月诞生的专注于梯度提升算法的机器学习函数库，此函数库因其优良的学习效果以及高效的训练速度而获得广泛的关注。XGBoost具有很多算法不具备的优势，不仅学习效果好、速度快，与梯度提升算法在另一个常用机器学习库scikit-learn中的实现相比，XGBoost的性能一般会有十倍以上的提升。

通俗来讲机器学习就是模型对数据的拟合，对于给定的一组数据，如果使用较为复杂的模型去处理，经常会发生过拟合的现象，此时就需要添加正则项来限制模型的复杂度，但是正则项的确定又是面临的一个新的难题，若选择较为简单的模型可能就很难达到理想的效果。相比而言，Boosting算法比较巧妙，首先使用简单的模型去拟合数据得，到一个比较一般的结果，然后不断向模型中添加简单模型(多数情况下为层数较浅决策树)，随着树的增多，整个Boosting模型的复杂度逐渐变高，直到接近数据本身的复杂度，此时训练达到最佳水平。

因此，Boosting算法要取得良好效果，要求每棵树都足够“弱”，使得每次增加的复杂度都不大，同时树的总数目要足够多。接下来将给出基于WRF-CMAQ和XGBoost的二次预报模型学习训练算法流程图5及关键步骤的分析。

Figure 5. WRF-CMAQ-XGBoost model flow chart

图5. WRF-CMAQ-XGBoost模型流程图

2.7. WRF-CMAQ-XGBoost模型的关键步骤

数据的选取以及训练集的划分和WRF-CMAQ-BP模型相同，下面给出随着参数的调整，MAE值的变化情况图：

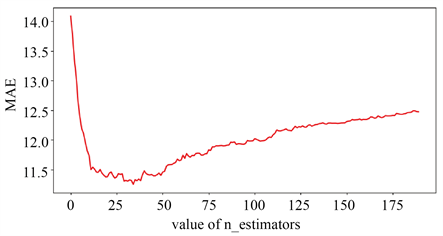
Figure 6. WRF-CMAQ-XGBoost model parameter adjustment

图6. WRF-CMAQ-XGBoost模型参数调整

从图6中可以看出，随着参数的调整，MAE值最小在5左右，远高于图3的MAE值，因此WRF-CMAQ-XGBoost模型的预测效果较WRF-CMAQ-BP模型而言是不具有优势的，所以在预测未来三天污染物的浓度模型选择上，本文选择WRF-CMAQ-BP模型。

3. 结语

本文提出了两个模型分别为WRF-CMAQ-BP和WRF-CMAQ-XGBoost模型，在构建网络后进行测试，在调参过程中发现WRF-CMAQ-BP模型的效果是更优的，因此本文用WRF-CMAQ-BP模型预测监测点A、B、C在2021年7月13日至7月15日六种常规污染物的单日浓度值。但是由于输入元的气象条件变量只有四个，可能还存在一些未考虑到的相关性比较强的气象条件，因此此模型还有待改进。

NOTES

¹本文中提及的附件1和附件2的数据来自2021年中国研究生数学建模竞赛B题附件1和附件2。