1. 引言
现代教育理论认为:“教学过程既是学生在教师指导下的认知过程,又是学生能力的发展过程。” [1] 在小学数学教育研究与实践中,不论哪一种数学教育理论,大都将学生对数学的认知程度作为评价教育效果的判据,这种认知程度体现在对数学基本概念、基本方法和有效运用的系统认知上。但是由于小学生在数学感知与认知上的差异性,在数学思维形成与学习过程中的不确定性等因素,造成数学教育教学的不确定性,并且这种不确定性直接影响小学数学教育的整体质量。本文运用“可拓学”思想 [2],从元认知教育角度提出了基于“可拓认知”的小学数学教育思想和教学方法,为求解数学教育中的不确定问题探索新的研究路径。
2. 小学数学教育的理论基础
2.1. 基于系统观的教育思维
数学教育是小学教育的重要内容,其教育方法论经历了从机械反映论的数学观转向多元的、经验的、系统的数学观,一直以来是中外数学教育讨论的热点话题 [3]。小学数学教育方法论建立在机械反映论基础之上,这种机械反映论遵循着简化论、分析论的基本原则,在培养学生数学能力上发挥了重要作用。数学教育的简化论(要素思维)认为,学生对每一个事物和现象的数学描述是由各个要素、单个部分组成,这些要素和部分指向特定的范畴,形成了一定的数学概念和方法。数学教育的分析论认为,数学描述问题的主要形式是分析思维,其基本意义在于:“让学生理解数学所刻画的事物和现象,需要运用归纳推理、演绎推理、证明等逻辑思维,也就是说,要经过仔细研究、逐步分析,最后得出明确结论。” [4]
19世纪初,一个新的世界观开始萌芽,出现了一系列新的假设,产生了与简化论和分析论相反的系统论。在系统论的影响下,研究者将数学教育与学习过程作为一个相互协同发展的系统,这个系统不是单纯知识的简单地整合和相加,而是体现各部分相互作用、相互依赖而形成的整体,从而形成了基于系统思维的现代数学教育方法论。
心理学家们认识到,简化论试图通过对数字运算与空间形式的反应来测量对数学的感知和认知,是从数学到数学的认知模式,而没有给学习者提供数学的现象特征感知。认知心理学家认为,数学教育行为学派的研究没有提供对数学整体反应的信息,没有为学习者提供数学与现实行为的互动。针对早期数学感知与认知特点,当代数学教育研究者也试图从系统论、信息论和控制论的综合角度探索有效的教育理论和教学模式,一些成熟的理论已经作为小学数学教育的基础理论和实践方法,但是数学教育的不确定性问题仍然没有解决。
2.2. 数学教育的元认知思想
数学是由数字、字母、符号、图形构成的表达现实世界数量关系和空间形式的科学。它不但是一门科学,还与语言、文化、艺术和哲学等相关联构成的思维综合体。因此,对于小学数学教育来说,不能仅仅将数学教育作为传授数学知识的形式,尤为重要的是要对数学的认知形式与过程的把握。从数学教育角度,学生在数学的认知上,不仅仅是对加、减、乘、除运算方法的了解和掌握,要让学生们知道,如何对一个运算形式、一种测量方法的了解和掌握。也就是说,不仅是从数学内容上,更重要的是从如何了解和掌握数学内容上来认知数学,这才是小学数学教育的根本,可称为数学教育的元认知思想。
实际上,数学教育的元认知思想包括教与学两个方面,即教育的教育,学习的学习。小学数学教育教学过程是一个自组织、自适应过程,通过这一过程,得到对学生、教学内容、教学方法和教学目标的不同程度认识,从而调整与优化符合实际要求的教育教学模式,体现的不仅是教育的内容和方法,而是如何实现教育内容与方法。
基础教育的核心问题是,通过教育教学过程使学生明确什么是学习。如果让孩子们了解和掌握了一门知识是如何学会的,那么他就能对学习产生兴趣,将学习融入快乐之中。这种从教育中学会教育,从学习中学会学习的教育理念是一种元认知教育。具体来说,小学数学认知教育是一个从不确定性到确定性的认知转化过程,这种认知转化是小学生认知能力培养的关键。
3. 从不确定到确定的认知转化
3.1. 转化与可拓的超循环特征
近些年,元认知教育理论在小学数学教育中得到了关注。一些研究者从不同角度验证了元认知教育在数学教育中的重要性。例如,项目教学法在小学数学教育中得到了较好的应用效果 [5],其实际意义是,将数学问题与现实生活和社会现象结合起来,让学生在数学的实际意义的感知中得到认知。不难发现,小学生的数学能力都是在对数学认知的认知中得到不断发展,而这种数学能力的形成过程是感知到认知的循环过程,这种循环是一种超循环 [6]。也就是说,这种超循环是在原有数学感知中进入新的数学感知,在数学感知能力的不断形成过程中产生数学认知。
在小学数学教育中,每一个数学知识学习过程都是一个有限次的感知过程(自循环),也就是重复性学习。在经历了解和掌握后进入新一个阶段的知识学习过程(新的自循环),这个新的自循环是前一个自循环的超循环。因此,小学数学教育中的每个阶段的学习过程都要完成从自循环到超循环的可拓认知过程。从概念转变理论也能得到这种感知与认知的超循环特征。在概念转变的教学实践中,强调学生前概念与科学概念相关本体的差异,通过对前概念的经验感知和相关概念的认知进入新的认知生态圈。从可拓认知的角度,这种概念转变的认知生态圈就是一种超循环的感知与认知系统。如图1所示。
3.2. 教与学中的转化机理
小学数学教育是一种教与学的行为系统,这种行为系统是复杂的,其复杂性体现在教与学的融合程度,这种融合程度包括学生感知与认知的转化程度,教师对学生学习的认知程度,以及教学过程的不确定性和确定性的转化程度。在传统的教学研究中,确定性教学是在消除不确定中形成的,但是如何消除不确定性则是一个较为困难的问题。引入超循环认知过程就是为消除不确定性提供了有效的方法。例如,一个确定性数学教学模式是在对不确定性教学过程的认知学习中产生的,教师在得到确定性教学认知的同时学生也得到了确定性的认知学习。可以认为,这种数学认知学习过程必须经过教学过程的超循环进行验证。
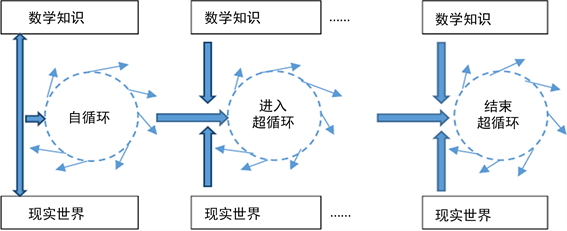
Figure 1. Mathematical cognitive process based on hyperloop
图1. 基于超循环的数学认知过程
目前,小学数学教育处于学生、教师和家长三者的博弈中,要确定一个三者都接受的教育教学模式是非常困难的。在家庭教育环境影响下,家长与教师在学生数学感知与认知上的信息不对称性,造成学生在数学学习行为与教师选择的教育行为之间的不确定性,这是需要通过可拓变换来解决这种不确定性。如果在学生数学教育方面实施了可拓变换功能,使数学教育中的不确定性通过可拓变换达到确定性,这样的数学教育就是一种可拓数学教育。例如,小学三年级的数学教育是建立记忆与联想的数学思维关键期(通常情况下的界定)。这一阶段能够基本确定学生的数学感知与认知能力。如图2所示。
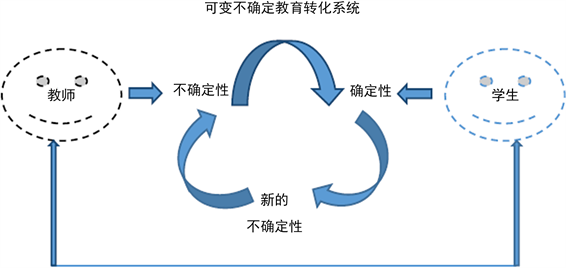
Figure 2. Adjustment process of uncertainty in primary mathematics education
图2. 小学数学教育的不确定性调节过程
因此在实际教育过程中,教师要根据学生对数学感知与认知特点,确定面向个体属性的教育教学模式。通过教学内容、教学方法、教学目标等可拓变换方式 [7],消除教育中的不确定性,来实现教与学的相互融合。在小学数学教育实践中,其教育与教学模式、教学方法并没有确定的标准,而是在不断调节教与学中的不确定性,达到学生、教师和家长共识情况下的确定性。小学数学教育不同于一般的知识传授,它是在有效的观察、模仿和实际体会中形成对数学的感知与认知,经过从无形到有形、有形到无形、无形再到有形的学习活动中,得到对数学的认知与能力。这种数学教育特点就是在教育过程中来认识教育、适应教育和发现新的教育,充分体现了在教育中发现教育的可拓认知思维。
4. 基于可拓认知的教学模式
如前所述,小学数学教育是一种基于可拓认知的元认知教育。这种数学教育的教学模式是根据对数学认知的可拓思维模式决定的,包括四种思维模式:发散性思维、相关性思维、蕴含性思维、共轭性思维。这些可拓思维模式符合个性化、多元化和智能化的小学数学教育的基本要求。
4.1. 发散性认知模式
发散性是事物可拓分析的最基本特性,也是元认知教育中的一种思维模式。无论是数学认知思维、数学教育思维还是数学学习思维,发散性思维是实现可拓认知的前提。实际上,就传统小学数学教育而言,发散性已经是一种成熟的教学思维模式。这里所说的发散性思维教学法,是指从不同角度进行思维,从不同层面进行分析,从而视野开阔,产生出大量的独特的新认知。而收敛性思维是指在教学中以一个方向聚敛前进,从而形成唯一的、确定的答案。例如8 + 5 = 13,就是具有收敛思维模式(集中教学法)。如果是:“还有哪些数相加也为13呢?”就有多种结论,这就是发散性思维教学法。在可拓数学教育中,基于这种发散性思维教学法更利于小学生创造性学习能力的培养。
4.2. 相关性认知模式
小学数学教育的特点不仅仅是单纯数学知识的传授,更重要的是数学知识与现实生活和生产劳动的相关性教育。数学相关性教育是一种联结教育,也体现了“同化”与“迁移”的学习特征。数学的认知过程是从发现整体,到探索部分,再到整体。数学形式与方法开始于对数学整体的感知,然后逐渐地变成个人的意识。在小学音乐教育过程中,整体与整体的相关性,部分与部分的相关性,以及整体与部分的相关性是不可缺少的内容,如果没有相关性思维的教育过程,真正理解和掌握数学的本质是不可能的。因此相关性思维教学法能够唤起学生从学习产生新的学习。
4.3. 蕴含性认知模式
蕴含的意义可以有多种理解。从词语解释角度,蕴含是动词,指一个词包含的内容,蓄积而未显露或发掘。从逻辑角度,蕴含表示一种规则,即如果一种情况发生,那么就会有另一种情况发生,反映了一种因果性。在“可拓认知”的数学教育领域,蕴含是数学知识的一个构成因素,建立了学生数学思想的各种意义层面。包括:1) 数学语言性;2) 数学艺术性;3) 数学文化性;4) 数学科学性、数学生活性,等等 [8]。通过蕴含性思维教学法,能够了解和掌握数学构成与发展中的因果关系。如果没有蕴含性思维教学法,对数学感知仅仅是盲目性的、无规则性的。蕴含性思维教学法能够从理性角度加深对数学学习的认识。
4.4. 共轭性认知模式
共轭性反映了事物一种对立特征,即正与负、实与虚、显与潜等,在事物转换与辩证分析中具有重要的作用。针对小学数学教育,共轭性思维能够使学生比较自然的进入学习环境,并且还能在对比中理解学习内容,发现学习问题。例如,数学感知是在无形的框架下对计算的认知,数字是可以比较和辨认多少的实体,但对于小学生来说,加、减、乘、除的运算形式不太容易理解其现实意义。因此针对这些看不到、摸不着的教学内容,需要共轭性思维。共轭性思维的数学教育是从实与虚、显与潜的角度去认知数学的构成意义,为开拓小学生数学认知提供了新的途径。
以上四种教学思维模式构成了基于“可拓认知”的小学数学教育教学思维系统。
5. 结语
在基于“可拓认知”的数学教育教学过程中,不论哪一种教学思维都是从不同角度解决教与学认知方面的不确定性。小学数学教育的本质是将教育教学建立在“可拓认知”思维基础上,通过对数学可拓认知模式的把握,形成了数学如何教、如何学的模式,即“可拓认知”下的元认知教育模式。研究表明,数学教育思想是从机械论、系统论而发展到可拓论,而小学数学教育的“可拓认知”是一种新的数学教育思想,其核心在于教育过程中的“可拓认知”。这种“可拓认知”体现了数学教育中的元认知教育理论,即对认知的认知、对教育的教育、对学习的学习。“可拓认知”教学模式为小学数学教育研究与实践提供了新的思维模式,作为从事小学数学教育的教师和研究者,要进一步研究“可拓认知”的教育教学理论与方法,将它应用到具体的教育教学实践中。同时,“可拓认知”思维模式可以对元认知教育理论进行深入的研究与实践,这也是当代教育理论亟待解决的问题。