长江流域夏季极端降水非平稳极值建模及其趋势分析

Non-Stationary Modeling and Trend Analysis of Extreme Precipitation in Summer over Yangtze River Basin

摘要: 使用国家气象信息中心位于长江流域共124个有效站点的降水资料，引入随时间变化的动态阈值，建立超门限广义帕累托分布模型，利用非平稳极值模型分析长江流域近57年(1961~2017年)夏季极端降水的时空特征及其趋势分析，并给出了重现期趋势变化情况。该分析对水源管理、水利建设以及城市设计等都具有重要的意义。1) 相对于平稳极值模型，非平稳极值模型能够更好地刻画极端降水；2) 给出了非平稳极值模型下极值模型参数分布情况，结果显示：长江流域尺度参数的趋势存在局部性，大部分地区趋势为正，形状参数呈现出正负相间的分布特征；3) 最后计算了20年、50年、100年一遇重现期趋势变化率，结果显示：不同重现期的降水量分布相似，重现期越长，极端降水重现水平最大的地方越多，重现水平达到了20 mm/decade以上；重现期均值也显示：相较平稳极值模型，非平稳极值模型极端降水的100年重现期所显示的重现水平更大，大的重现水平的区域范围增加。

Abstract: Using the precipitation data of 124 effective stations located in the Yangtze River Basin by the National Meteorological Information Center, the dynamic threshold varying with time is introduced, and the over threshold generalized Pareto distribution model is established. The temporal and spatial characteristics and trend analysis of summer extreme precipitation in the Yangtze River Basin in recent 57 years (1961~2017) are analyzed by using the non-stationary extreme value model, and the trend change of return period is given. The analysis is of great significance to water source management, water conservancy construction and urban design. 1) Compared with the stationary extreme value model, the non-stationary extreme value model can better describe extreme precipitation; 2) The results show that the trend of scale parameters in the Yangtze River Basin is local, the trend is positive in most areas, and the shape parameters show the distribution characteristics of positive and negative phases; 3) Finally, the trend change rates of 20-year, 50-year and 100-year return periods are calculated. The results show that the precipitation distribution in different return periods is similar. The longer the return period, the more places with the largest return level of extreme precipitation, and the return level reaches more than 20 mm/decade; the mean value of return period also shows that compared with the stationary extreme value model, the 100-year return period of extreme precipitation in the non-stationary extreme value model shows a larger return level, and the regional range of large return level increases.

1. 引言

气候变化是当今全球共同面临的重大课题，IPCC第6次评估报告指出，近百年来全球气候正经历一次以变暖为主要特征的显著变化，持续的温室气体排放是造成气候变暖的重要原因之一。在全球变暖背景下，气候变化不仅表现在气候平均态的变化上，也包括极端天气事件的变化。随着全球气候变暖，地球上的极端天气事件就已经开始增多，包括强降雨、热浪、洪水、干旱、强台风等极端天气气候事件的发生频率和强度呈现增加的趋势 [1] [2]。相对于气候平均态，频繁的极端天气气候事件给生态环境、经济发展和人民生活更是造成了严重的影响和损失 [3]。作为人口大国及农业大国，中国更容易受到极端降水的影响，这很可能造成巨大的社会、经济损失和生态系统的破坏。因此，考虑中国未来极端降水的强度、延时、频率变化情况，管理好水资源、农业活动、民用基础设施建设以及其他人类活动显得尤为重要 [4]。

极端降水开展了较多的工作，国内来看，中国区域强降水变化态势整体上与全球是基本一致的，同样存在着区域性差异和局地性明显特征 [5]。全国总的降水量变化趋势不明显，雨日显著减少，毛毛雨显著减少 [6]。从区域性变化看，长江流域降水趋于增多，华北地区降水趋于减少，同时伴随着雨日的显著减少，这意味着降水过程可能呈现强化的趋势，干旱与洪涝灾害趋于增多 [7]。中国区域极端强降水平均强度和极端降水值都有增强的趋势，极端强降水事件也趋于增多，尤其在20世纪90年代，极端强降水量比例趋于增大，说明降水量可能存在向极端化方向发展的趋势 [8]。

翟盘茂等 [9] 以日降水量序列的第95个百分位数定义极端强降水，研究发现从极端强降水量来看，华北地区强降水量值趋于减弱，西北西部无明显变化，长江及长江以南地区趋于增多；从极端强降水日数来看，我国西部地区和长江中下游至华南地区表现为增加趋势，而东北和华北以及四川盆地呈现减小的趋势；从极端强降水事件发生频率和极端强降水平均强度来看，华北地区发生频率呈现明显减少的趋势，但强度有所增加，西北西部地区强降水事件发生频率趋于增加，但强度明显变化，而在长江及其以南地区强降水事件频率和强度都呈增大的趋势。王志福等 [10] 则对中国持续不同天数的极端强降水事件的频数和强度研究发现，持续1天极端事件的相对频数具有上升趋势，其空间上均表现为全国大部分上升，持续2天以上极端事件在长江中下游流域、江南地区和高原东部等地区有显著增多和增强的趋势。白路遥 [11] 分析了最近50年长江流域的极端降水特征，结果表明，整个长江流域各种极端降水量指标的空间差异明显，区域平均年降水量和极端过程降水随时间没有明显的线性趋势；长江上游和中游一带极端频率指标中存在显著非线性增大趋势，四川盆地和下游地区极端频率的非线性趋势不明显。极端降水量大的区域，极端指标出现频率也很高，对年降水量贡献很大，是产生洪涝灾害的重要原因。

对极端降水的分析多基于线性回归、Mann-Kendall等趋势分析方法，极值模型则采用广义极值分布 (generalized extreme value distribution, GEV)和广义帕累托分布(generalized Pareto distribution, GPD)分析极端降水分布特征。荣艳淑等 [12] 利用广义极值分布理论估算了淮河流域的重现期降水量，结果表明：在空间上，半湿润气候区有更强极端降水过程，而湿润气候区降水极端性偏小；在时间上，降水偏多的年代，极端降水量和极端降水过程更多，降水偏少的年代，极端降水指标数值偏小；重现期时间尺度存在临界点，在临界点以下，各站重现期降水量都会明显增大，超过临界点，淮河流域上游和南部重现期降水量变化很小，而中游、下游和北部重现期降水量增大明显。杜鸿等 [13] 运用广义极值分布和广义帕累托分布两种极值统计模型对规范化样本进行拟合，分析淮河流域极端径流的时空变化规律。检验发现，GEV和GPD分布分别能有较好的拟合效果。

不难发现，对于极端降水大量的分析主要基于平稳模型，而利用平稳模型计算水利设计的重现期，往往存在低估，这在极端降水频率增加时，更会造成设计不符合实际需求的状况。因此，本文引入时变阈值，通过构建非平稳极值模型，来分析极端降水趋势特征以及重现期趋势特征，并对比固定阈值情形和平稳极值模型，从而得出平稳模型确实存在低估重现期的情形。

本文主要内容如下，第二部分介绍数据来源与方法，第三部分给出分析结果，第四部分得出结论。

2. 数据与方法介绍

2.1. 数据选取

本文所用数据为中国国家气象局(CMA)国家气象信息中心(NMIC)提供的1951~2017年横跨中国756个气象站的日降水数据。这个数据集的质量已由NMIC控制并约束，是目前最好的日数据集并被广泛应用于气候变化研究 [14]。由于50年代有较多缺失数据，本文选取1961~2017年的降水数据进行研究，再去掉1961~2017年一些缺失了6~8月份(JJA)观测数据的站点，一共得到长江流域124个站点的观测数据，其分布情况见图1，六个代表站用红色标示。可以看出，这些站点由西向东覆盖了整个长江流域，而且跨越了长江南北两侧的区域。站点均匀地分布在中国东部平原，甚至包括了位于中国西北地区的青藏高原和塔里木盆地。

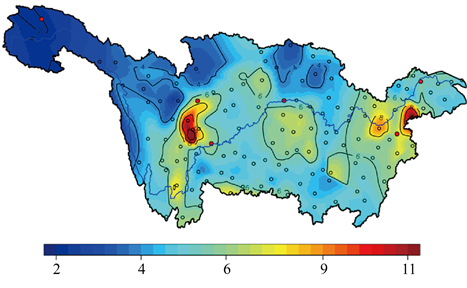
Figure 1. Location distribution of 124 observation stations (6 representative stations) and spatial distribution map of average precipitation (mm/d)

图1. 124个观测站(6个代表站)位置分布以及降水平均值空间分布图(mm/d)

2.2. 方法

2.2.1. 平稳GPD描述

广义Pareto分布(GPD)是专门用来描述超过一个临界值(阈值)的所有观测值资料的概率分布特征，它的分布函数是：

$P\left(X\le x\right)=1-{\left(1+\frac{\xi x}{\sigma }\right)}^{\frac{1}{\xi }}x>0,1+\frac{\xi x}{\sigma }>0$ (1)

其中， $\sigma$ 是尺度参数，它起放大或缩小分布面积的作用，描述极值分布的变率，尺度参数越大，表明极值波动范围越大； $\xi$ 是形状参数，描述极值的分布情况， $\xi <0$，GPD是薄尾的，表示分布有上限， $\xi >0$，GPD是厚尾的，表示分布没有上限 [15]，阈值为0。

2.2.2. 非平稳GPD

1) 动态阈值定义与选择

选取阈值是极其重要而复杂的过程，尤其当观测序列较短时，往往要在极值足够大和超出量样本足够多之间保持合理的平衡。太大的阈值将导致可用数据量变少，从而导致参数估计量的方差偏大；阈值太小将使估计量成为有偏估计，不能满足GPD分析的条件(万仕全等，2010)。本文采用动态阈值，即随时间变化的阈值，来确定各个站点日降水量的百分位点。

对于每个季节

$u\left(t\right)=m\left(t\right)+\alpha$ (2)

其中 $m\left(t\right)=a+b\left(t\right)$，表示每次降水事件的平均降水量， $\alpha$ 为 $\left\{\left[DR\left(t\right)-m\left(t\right)\right]|DR\left(t\right)>m\left(t\right)\right\}$ 的百分位数，是超出平均降水量 $m\left(t\right)$ 的数据分位点。这种方式能够保证超过阈值以上的数量相同，类似于选择降水量的95%分位点， $DR\left(t\right)$ 是观测站的日降水。由于阈值 $u\left(t\right)$ 对任意给定年份要相同， $m\left(t\right)$ 可以认为是每年的平均值，从而可以得到超过阈值的极端降水样本。

2) 非平稳极值模型

设 $X=DR\left(t\right)-u\left(t\right),DR\left(t\right)>u\left(t\right)$，则 $X$ 服从GPD分布如下：

$F\left(x\right)=1-{\left[1+\frac{\xi \left(x-u\right)}{\sigma }\right]}^{-\left(\frac{1}{\xi }\right)},\xi \ne 0$ (3)

式中 $x=DR\left(t\right)$ 是日降水， $u=u\left(t\right)$ 是随时间变化的阈值。满足如下条件：

$x\ge u$ (4)

$1+\frac{\xi \left(x-u\right)}{\sigma }>0$ (5)

其中 $\sigma$ 为尺度参数， $\xi$ 为形状参数，形状参数值小于零说明分布有上限，大与或等于零说明分布没有上限。

因为本文的目标是研究极端降水的实时变化，GPD模型的参数与时间相关，利用极大似然法估计参数，GPD分布的对数似然函数如下：

$L\left(\theta \right)=L\left(\sigma ,\xi \right)=n\ln \xi -n\ln \sigma -\left(\frac{1}{\xi }+1\right){\displaystyle \underset{i=1}{\overset{n}{\sum }}\ln \left(1+\frac{\xi }{\sigma }{x}_i\right)}$ (6)

在模型的参数中添加时间变化项：

$\xi \left(t\right)=\xi ,\ln \left(t\right)={\sigma }_0+{\sigma }_{1}t$ (7)

在式(7)条件下，重现水平也与时间有关，用分位数或者重现水平的方法解释极端值对水资源的分配利用具有重要作用。重现水平是出现气候稀有事件(气候极值)概率的气候变量的可能取值，而出现极值的概率的倒数就是重现期。对于不同概率下(重现期)的重现水平有分布函数：

$F\left(x_N\right)=1-\frac{1}{\rho N}$ (8)

$\rho =n{\zeta }_u$ 是每年超过阈值的平均样本数，GPD重现水平的估计式为：

$x_N\left(t\right)=u\left(t\right)+\frac{\sigma \left(t\right)}{\xi }\left[{\left(N\rho \right)}^{\xi }-1\right],\xi \ne 0$ (9)

若已知重现水平，则其重现期的估计式为：

$N\left(t\right)={\left\{\left[x_N-u\left(t\right)\right]\frac{\xi }{\sigma \left(t\right)}+1\right\}}^{\frac{1}{\xi }}/\rho$ (10)

其中， $N$ 是重现期(年)， $n$ 是每个季节的观测数， ${\zeta }_u$ 是超过阈值 $u$ 的可能性，也是超过阈值的样本数与总观测数的比值。

重现水平随时间变化的趋势 ${\beta }_{N,t}=\frac{\partial x_{N,t}}{\partial t}$ 也是一个关于时间的函数，取其滑动平均值作为估计值：

${\bar{\beta }}_N=b+\frac{\exp {\sigma }_0}{\xi }\left[{\left(Nn{\zeta }_u\right)}^{\xi }-1\right]\frac{1}{\Delta }\left(\exp \left({\sigma }_1{t}_f\right)-\exp \left({\sigma }_1{t}_i\right)\right),\Delta =t_f-t_i$ (11)

$t_i,t_f$ 分别为重现期开始和结束的时间， $b$ 是每个季节降水量均值的线性回归方程的斜率。用(11)式计算重现水平包含两个方面：一是长期的平均降水趋势 $b$，可以解释为降水量中心值变化指标，另一个是尺度参数 ${\sigma }_{\text{1}}$，它提供了出现极端降水极大值概率的趋势变化信息( ${\sigma }_{\text{1}}>0$ 表明出现降水极大值的概率增加， ${\sigma }_{\text{1}}<0$ 表明概率减小)。 $\left[{\left(Nn{\zeta }_u\right)}^{\xi }-1\right]/\xi$ 恒大于零且与 $\xi$ 的正负无关，(11)式第二项的正负取决于 ${\sigma }_{\text{1}}$。如果斜率和尺度参数都大于零，则重现水平随时间增加；若二者都小于零，则重现水平随时间减小；若二者一正一负，则取决于哪个处于主导地位 [16]。

3. 主要结果

3.1. 时变阈值选取

我们用阈值和随时间变化的GPD模拟极端降水事件。本文选取具有代表性的南京、景德镇、奉节、都江堰、宜宾、五道梁这六个站点反映阈值变化与样本选取的关系。如图2所示，图中空心圆表示日降水的分布，红色直线表示随时间变化的阈值，由均值趋势线与分位点后的值相加而得，红线上方为通过阈值筛选的样本点。

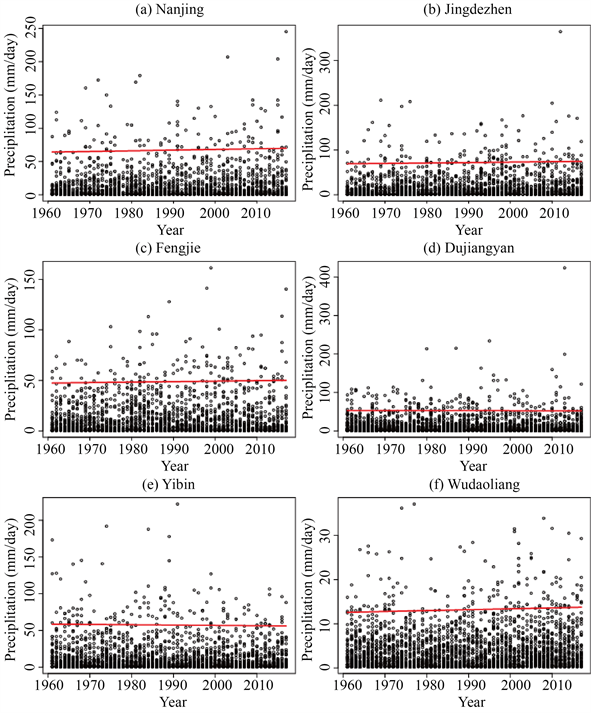
Figure 2. The time series of day precipitation for the six representative stations and the corresponding the u(t) (which are shown in the red line)

图2. 6个代表站日降水分布散点图及阈值u(t) (红线)

图3(a)反映了长江流域各站点的平均阈值(等值线)、阈值随时间变化趋势的空间分布(阴影)和通过显著性检验的站点。图中蓝色三角表示站点呈正显著，蓝色圆圈表示正不显著，红色三角表示负显著，红色圆圈为负不显著。平均阈值的分布与中位数的分布相似，整体来看，长江中下游地区平均阈值较大，说明此处的平均降水量较大，尤其是重庆东北部、湖北东北部、安徽边缘、江苏、浙江、上海及福建等地降水量呈上升趋势；阈值较小的地方位于长江流域上游，甘肃、四川盆地降水呈下降趋势。时变阈值中，包含信息量更多的部分是由线性回归给出的斜率，图3(b)显示了各观测站点m(t)中趋势的直方图。可以明显地看出，绝大部分趋势呈现正值，只有一小部分为负值，这与趋势分布图的结果一致。

因此，长江流域的日降水量随阈值的变化存在趋势性变化，如果采用平稳极值模型，不考虑阈值的变化是不合理的。

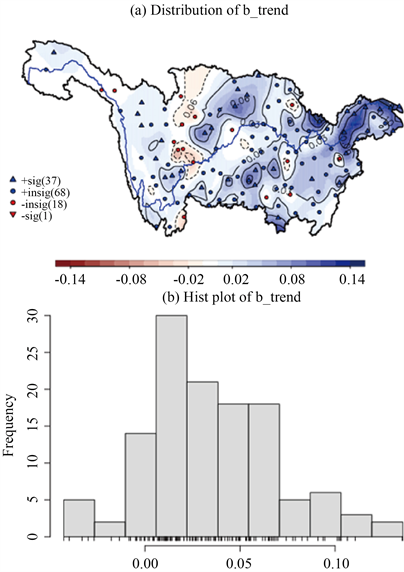
Figure 3. The spatial distribution (a) and histogram (b) plot for the b_trend of 124 stations

图3. 124个站点均值降水趋势系数空间分布图以及趋势系数条形图

3.2. GPD分布构建

3.2.1. 六个代表站GPD分布模拟情况

表1选取了南京、景德镇、奉节、都江堰、宜宾和五道梁六个代表站点展示其分别在平稳和非平稳GPD模式下的参数估计和对应方差，不难看出，平稳GPD模型的结果与非平稳模型有很大的差别。在考虑时变阈值的非平稳模式下，除都江堰站外各个站点的趋势系数均通过了显著性检验，说明考虑了时间变化的GPD模型是正确且有必要的。

Table 1. Stationary and non-stationary estimated parameters (standard errors in parentheses) of GPD

表1. 平稳与非平稳GPD分布的参数估计(括号内为标准差)

3.2.2. 空间场参数估计

由GPD模型所拟合的我国长江流域各站逐日超过阈值的极端降水量概率分布的统计参数在地理空间上的分布特征绘于图4、图5，图4为考虑时间变化的非平稳GPD模型(GPD-tt)，而图5为平稳GPD模型(GPD-cc)的参数分布情况。其中，图4(a)、图5(a)为超过阈值的日极端降水量的均值，图4(b)、图4(c)、图5(b)为尺度参数及其趋势的空间分布，图4(d)、图5(c)为形状参数的空间分布。由图可见，考虑时间变化后，长江流域下游平均尺度参数较大，中心位于陕西安康附近，出现降水极大值的可能性很大。总的来看，长江流域尺度参数的趋势存在局部性，大部分地区趋势为正，在五道梁，曲麻莱，清水河及青海省南部地区呈现负趋势，此外，四川道孚、小金等地尺度参数趋势为负，表明这些地方趋势降低较明显，即降水极大值出现的概率是减小的；反之，在平稳GPD模式下，长江流域平均尺度参数的大值区域增多，如四川都江堰、峨眉山附近，湖北广水，安徽滁洲、景德镇，江西九江等地，出现降水极大值的概率很大。

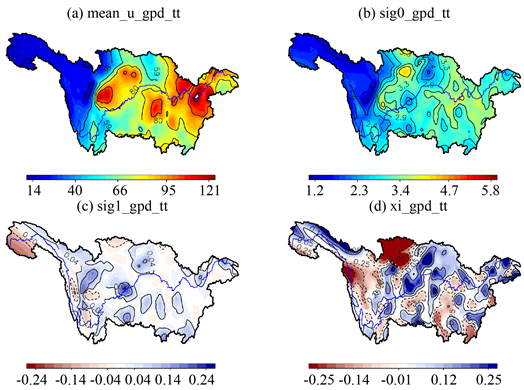
Figure 4. The spatial distribution of u, σ₀, σ₁ and mean field over threshold for the GPD-tt fitting of 124 stations

图4. 124个站点GPD-tt拟合的u，σ₀，σ₁分布图以及超过阈值均值场图

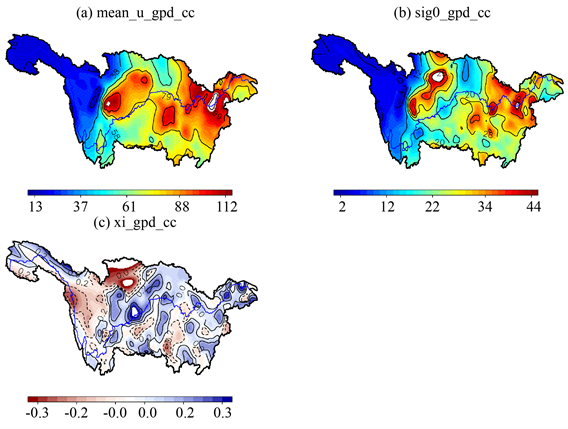
Figure 5. The spatial distribution of u, σ₀ and mean field over threshold for the GPD-cc fitting of 124 stations

图5. 124个站点GPD-cc拟合的u，σ₀分布图以及超过阈值均值场图

对于形状参数，考虑时间变化后，整个长江流域形状参数呈现出正负相间的分布特征，在甘肃南部，陕西南部，四川东北部及东部部分地区为低值中心，陕西东南部，重庆东北部，五道梁，曲麻莱，清水河等地为高值中心；如果不考虑时间变化，与非平稳GPD模型相比，形状参数的空间分部表现出很明显的差异。

3.3. GPD重现期趋势分析

图6给出长江流域所选124个站点在重现期为10年、30年、50年和100年的极端降水重现水平情况。即分别以10年、30年、50年和100年为周期时，可能达到的极端降水的降水量。可以看出，不同重现期的降水量分布相似，极端降水重现水平最大的地方出现在湖北东南、安徽西部、江西北部周围，重庆大部、四川中部及贵州、湖南、广东部分地区，重现期越长，极端降水重现水平最大的地方越多，重现水平达到了20 mm/decade以上。

图7对比了6个代表站在平稳模式和非平稳模式下随着重现期的增加，极端降水重现水平的变化情况。可以看出，虽然在较短的重现期内，不考虑时间变化的GPD模型所反映的极端降水重现水平与时变性的GPD模型基本相同，但随着重现期变长，常数阈值与时变阈值反映的重现水平波动会有明显差别。因此，非平稳极值模型的运用有其必要性及正确性。

图8给出重现期为50、100年非平稳极值模式下极端降水重现水平的空间分布情况，及平稳与非平稳极值模式的比较。可见，对于非平稳模型，100年重现期与50年相比，极端降水的重现水平分布基本相同，但100年重现期所显示的重现水平更大，大的重现水平的区域范围增加。比较平稳和非平稳模型可以看出，在数据观测起始年份，在四川中部，陕西南部，重庆西部，安徽西部等地，平稳极值模型的极端降水的重现水平大于非平稳极值模型，而在数据观测终止年份，重现水平的情形正好相反。

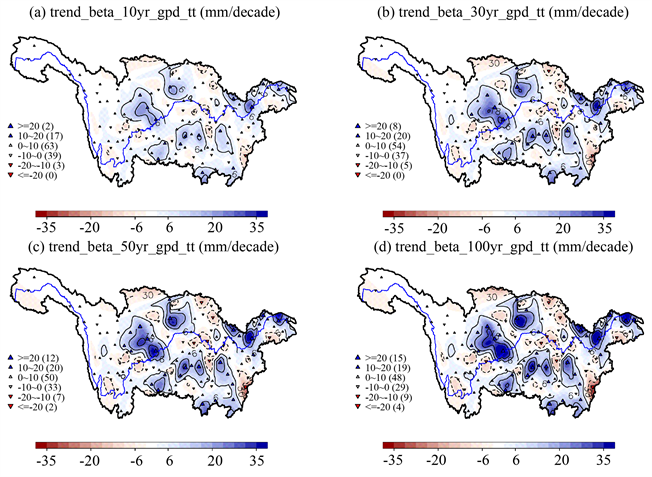
Figure 6. Spatial distribution of the trends in the 10, 30, 50 and 100-yr return level for the GPD-tt fitting of 124 stations

图6. 124个站点GPD-tt拟合的10，30，50及100年重现期趋势空间分布图

Figure 7. Return period curve for 6 representative stations

图7. 6个代表站重现期曲线

Figure 8. Spatial distribution of 50, 100 years return period of non-stationary extreme value model and difference from that of stationary extreme value model

图8. 非平稳极值模式重现期50，100年重现水平的空间分布及其与平稳极值模式情形的差异

4. 结论

本文引入随时间变化的动态阈值，建立超门限广义帕累托分布模型，利用非平稳极值模型分析长江流域近57年(1961~2017年)夏季极端降水的时空特征及其趋势分析，并对比平稳极值模型，给出了重现期趋势变化情况。

1) 长江流域的日降水量随阈值的变化存在趋势性变化，如果采用平稳极值模型，不考虑阈值的变化是不合理的，因此需要采用考虑动态阈值的非平稳极值模型；

2) 在非平稳模型模拟下，长江流域下游平均尺度参数较大，中心位于陕西安康附近，出现降水极大值的可能性很大。长江流域尺度参数的趋势存在局部性，大部分地区趋势为正，此外，四川道孚、小金等地尺度参数趋势为负，表明这些地方趋势降低较明显，即降水极大值出现的概率是减小的；

3) 不同重现期的降水量分布相似，极端降水重现水平最大的地方出现在湖北东南、安徽西部、江西北部周围，重庆大部、四川中部及贵州、湖南、广东部分地区，重现期越长，极端降水重现水平最大的地方越多，重现水平达到了20 mm/decade以上。与平稳极值模型相比，100年重现期所显示的重现水平更大，大的重现水平的区域范围增加。