恰当使用数学工具提升物理学习能力

Improve the Ability of Physics Learning via the Proper Use of Mathematical Tools

摘要: 本文分别从变力冲量的计算、极值类问题的求解、洛伦兹力方向的确定、弹簧振子周期公式的推导四方面，比较了高中物理与大学物理在使用数学工具上的差别。结果表明，物理学的发展促进了数学工具的变革，数学工具又反作用于物理学，不同阶段的物理学需要特定等级的数学工具与之相适应，这对于学生学习不同阶段的物理学具有一定的指导意义。

Abstract: In this paper, the differences between high school physics and college physics in the use of ma-thematical tools are compared from four aspects: the calculation of variable force impulse, the solution of extreme value problems, the determination of Lorentz force direction and the derivation of spring vibrator period formula. The results show that the development of physics promotes the reform of mathematical tools, and the mathematical tools react on physics. Physics in different stages needs specific levels of mathematical tools to adapt to it, which has certain guiding significance for students to learn physics in different stages.

1. 引言

物理学是一门以实验为基础，研究物质运动最基本、最一般的规律和物质的基本结构，以及它们的应用的自然科学。高中物理主要涵盖了力学、光学、热学、功与能的转化、电磁学等方面的基础知识。相比于初中物理而言，内容更为宽广深奥，解决问题的策略更加灵活，这主要得益于高中数学矢量运算及三角函数知识的深入学习。大学物理是高中物理在各个方面的拓展，这主要得益于高等数学知识的学习，这也正是牛顿创立微积分的初衷。微积分已融入大学物理的各个知识章节 [1] [2] [3] [4]。

数学是物理学的语言和工具，数学工具对物理学科的学习至关重要。在中学阶段，我们知道了大多数物理问题可归化为解方程或方程组的方式来解决，于是思维方式进入初等数学的阶段。等到进入大学，我们开始了微积分的学习，思维方式发生了转变，开始习惯用公理化的方式来思考物理问题。公理化的优点在于数学推理过程的严格性，不存在歧义。借助高等数学这一工具，我们发现以前所有的计算方法真的变得合理起来。初等数学主要研究的是常量与线性变量，而高等数学研究的是非线性变量。物理世界的本原是非线性的，中学阶段的线性理论只是一种近似而已。如果进入大学后，我们的思维仍然停留在初等数学阶段，学习高等数学只是满足获得相应的学分，不能恰当使用这一数学工具，那么物理课程的学习将会变得举步维艰。

目前，我国大学毛入学率已超过50%，实现了高等教育普及化。有很大一部分高中毕业生进入高等学校后要学习大学物理。因此，如何做好高中物理与大学物理的有效衔接，使得大学生能尽快适应大学物理的学习，或在学习大学物理的进程中少走弯路，这对于大学物理初学者及教育工作者都提出了新的挑战 [5] [6] [7] [8]。

在处理实际物理问题时，高中阶段我们习惯于初等数学思维分析问题，而大学阶段我们多了一些理性，习惯于系统思维，学会了用高等数学这一工具来分析问题。以下四个问题均出自于大学物理教材，我们不妨比较一下高中物理与大学物理在使用数学工具上的差别。

2. 计算变力的冲量

案例1：一物体质量为10 kg，受到方向不变的力F = 30 + 40t (SI)作用，在开始的两秒内，求此力冲量的大小？若物体的初速度大小为10 m/s，方向与力的方向相同，则在2 s末物体速度的大小？

高中阶段我们这样分析：这是求变力的冲量，显然已经超出了高中生的认知范围，经过类比后，我们发现冲量与求匀变速直线运动的位移有异曲同工之处，位移是速度在时间上的累积效应，且匀变速直线运动中速度随时间是线性变化的。此处，冲量是力对时间的累积效应，且作用力随时间也是线性变化的。因此，通过类比法可计算出变力的冲量，即冲量的大小等于力的变化线与坐标轴围成的面积，如图1所示。

Figure 1. Impulse obtained by “area method”

图1. “面积法”求冲量

$I=S_{梯形}=\frac{30+110}{2}\times 2=140\text{N}\cdot \text{s}$ (1.1)

大学阶段我们这样分析：冲量是力对时间的累积效应，只需知道作用力随时间的变化规律，无论作用力是否随时间作线性变化，直接采用积分的方法，即可计算变力的冲量。

$I={\displaystyle {\int }_0^{t}F\cdot \text{d}t}={\displaystyle {\int }_0^2\left(30+40t\right)\text{d}t}=140\text{N}\cdot \text{s}$ (1.2)

第二问直接使用动量定理即可正确求解。从此题可以看出，当变力F随时间线性变化时，我们利用等效面积可以求解。因为变力与坐标轴所围成的图形一般是三角形或梯形。延伸一下，如果力随时间非线性变化，则“面积法”失效，我们必须借助高等数学积分的思想，方能正确求解。

3. 极值类问题

案例2：一质量为m的物体放置在水平桌面上，在斜向上的拉力F作用下做匀速直线运动，已知物体与桌面间的动摩擦因数为 $\mu$ ，试问力F沿什么方向拉力最小？

Figure 2. Schematic diagram of force analysis

图2. 受力分析示意图

首先，对物体进行受力分析，如图2所示。因为物体做匀速直线运动，所以物体受到的力是平衡的。即，水平方向满足 ${\displaystyle \sum F_x=0}$ ，

$T\cos \theta -F_f=0$ (2.1)

竖直方向满足 ${\displaystyle \sum F_y=0}$ ，

$T\sin \theta +F_N-G=0$ (2.2)

加之牵连关系，

$F_f=\mu F_N$ (2.3)

联立上述3式，解得：

$T=\frac{\mu mg}{\cos \theta +\mu \sin \theta }$ (2.4)

高中阶段我们这样分析：欲求T的最小值，即求函数 $f\left(\theta \right)=\cos \theta +\mu \sin \theta$ 的最大值，我们一般采用辅助角公式，令 $\mu =\tan \varphi$ ， $f\left(\theta \right)$ 可改写为：

$f\left(\theta \right)=\cos \theta +\mu \sin \theta =\sqrt{{\mu }^2+1}\cos \left(\varphi -\theta \right)$ (2.5)

式中 $\varphi =\arctan \mu$ ，将式(2.5)代入式(2.4)，T的表示式改写为：

$T=\frac{\mu mg}{\sqrt{{\mu }^2+1}\cos \left(\varphi -\theta \right)}$ (2.6)

当 $\theta =\varphi =\arctan \mu$ 时，

$T_{\min }=\frac{\mu mg}{\sqrt{{\mu }^2+1}}$ (2.7)

大学阶段我们这样分析：欲求T的最小值，即求函数 $f\left(\theta \right)=\cos \theta +\mu \sin \theta$ 的最大值。按照求极值的基本方法，首先从方程 $f^{\prime }\left(x\right)=0$ 求出在函数 $f\left(x\right)$ 定义域内所有可能的极值点，然后按照函数极值的定义判断在这些点处是否取得极值。具体解法如下，

$f^{\prime }\left(\theta \right)=-\sin \theta +\mu \cos \theta =0\theta \in \left[0,\text{π}/2\right]$ (2.8)

解得：

$\theta =\arctan \mu$ (2.9)

此外，当 $\theta <\arctan \mu$ 时， $f^{\prime }\left(x\right)>0$ 时； $\theta >\arctan \mu$ 时， $f^{\prime }\left(x\right)<0$ 。

即：当 $\theta =\arctan \mu$ 时，

$f_{\max }\left(\theta \right)=\frac{1}{\sqrt{{\mu }^2+1}}+\mu \frac{\mu }{\sqrt{{\mu }^2+1}}=\sqrt{{\mu }^2+1}$ (2.10)

这样就获得了与式(2.7)相一致的结果。对比高中阶段与大学阶段的思维模式，我们不难看出：对于极值类问题的求解，运用高等数学知识求解更具有一般性，尤其对于处理高次方问题，高中阶段几乎无法处理，这时高等数学求极值的优点将得到彰显。

4. “左手定则”与“右手螺旋法则”的统一

案例3：一带正电的粒子，沿垂直于磁场的方向射入一匀强磁场。求带电粒子在磁场中所受洛伦兹力的方向如何？

高中阶段我们这样分析：如何确定带电粒子在磁场中的受力方向？应采用洛伦兹力判别法，即“左手定则”。具体操作是：将左手掌摊平，让磁感应线穿过手掌心，四指与正电荷运动方向保持一致，则和四指垂直的大拇指所指方向即为洛伦兹力的方向，如图3所示。值得注意的是，运动电荷带正电，大拇指的指向即为洛伦兹力的方向。反之，如果运动电荷带负电，仍用四指表示电荷运动方向，那么大拇指的指向的反方向为洛伦兹力方向。

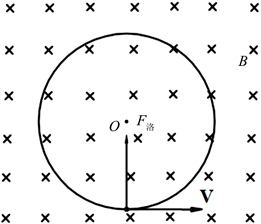
Figure 3. “Left-hand rule” to determine the direction of Lorentz force

图3. “左手定则”确定洛伦兹力的方向

大学阶段我们这样分析：洛伦兹力的矢量表达式为 $\stackrel{\rightharpoonup }{F}=q\stackrel{\rightharpoonup }{v}\times \stackrel{\rightharpoonup }{B}$ 。式中 $q$ 的正负决定于粒子所带电荷的正负。由上式可以看出，洛伦兹力 $\stackrel{\rightharpoonup }{F}$ 总是与带电粒子运动速度 $\stackrel{\rightharpoonup }{v}$ 的方向垂直，即洛伦兹力垂直于速度 $\stackrel{\rightharpoonup }{v}$ 和磁感应强度 $\stackrel{\rightharpoonup }{B}$ 所确定的平面。怎样确定洛伦兹力的方向，具体操作就是：右手的四指从 $\stackrel{\rightharpoonup }{v}$ 以不超过180度的转角转向 $\stackrel{\rightharpoonup }{B}$ 时，竖起的大拇指的指向就是洛伦兹力 $\stackrel{\rightharpoonup }{F}$ 的方向，如图4所示，两者结果一致。

对于洛伦兹力方向的确定，既可以使用高中阶段的“左手定则”，也可以使用大学阶段的“右手定则”，两者在本质上是一致的，这样就实现了“左手定则”与“右手定则”的辩证统一。

Figure 4. Schematic diagram of vector cross product

图4. 矢量叉乘运算示意图

5. 弹簧振子周期公式的推导

案例4：如图5所示，是一个弹簧振子的模型，其中金属杆光滑，轻质弹簧质量远小于金属小球的质量，试推导弹簧振子周期公式。

高中阶段我们这样分析：课本直接给出了简谐运动的振动方程 $x=A\cos \left(\omega t+{\varphi }_0\right)$ 。我们可采用“转换法”求解弹簧振子周期公式。如图5所示，弹簧振子在 $A$ 与 $-A$ 之间振动，

初始位置位于最右端点A处，即初相 ${\phi }_0=0$ 。其振动方程为： $x=A\cos \omega t$ 。如图6所示，线段OP绕点O，以角速度 $\omega$ 作逆时针旋转，我们发现线段OP在x轴上的射影也满足方程 $x=A\cos \omega t$ 。因此，简谐振动可以看成匀速率圆周运动的半径在水平方向的投影。

匀速圆周运动中，周期和角速度之间的关系：

$T=\frac{2\text{π}}{\omega }$ (4.1)

弹性绳的弹力提供小球圆周运动的向心力，

$kr=mr{\omega }^2$ (4.2)

联立以上2式可得：

$T=2\text{π}\sqrt{\frac{m}{k}}$ (4.3)

大学阶段我们这样分析：水平放置的弹簧振子，回复力仅由弹簧弹力提供。由牛顿第二定律可知：

$F=-kx=m\frac{{\text{d}}^{2}x}{\text{d}{t}^2}$ (4.4)

移去第一项，整理得，

$\frac{{\text{d}}^{2}x}{\text{d}{t}^2}+{\omega }^{2}x=0$ (4.5)

式中 $\omega =\sqrt{k/m}$ ，这是一个二阶常系数齐次线性微分方程，其通解为：

$x=C_1\cos \omega t+C_2\sin \omega t$ (4.6)

借助辅助角公式可得，

$x=A\cos \left(\omega t+{\phi }_0\right)$ (4.7)

式中 $A$ 和 ${\phi }_0$ 是由初始条件确定的常数。这样我们就获得了高中课本中直接给出的简谐运动的振动方程，求周期公式也就水到渠成了。

Figure 5. Schematic diagram of spring oscillator

图5. 弹簧振子示意图

Figure 6. Schematic diagram of line segment counterclockwise rotation

图6. 线段OP逆时针旋转示意图

对比高中阶段与大学阶段的两种解题方法，其差异性显而易见，高中阶段的解题方式比较直观，但需要一定的技巧性，一般同学根本发现不了简谐运动与同周期匀速率圆周运动之间的联系，大学阶段的解题方法借助了高等数学知识，解题的理论性更强，适用范围更广。

6. 总结

本文研究了高中物理与大学物理所使用的数学工具的差别。不同等级的数学工具适应于不同阶段的物理学。高中物理侧重初等数学思维，即数学技巧与代数运算的有机结合；而大学物理侧重系统思维，如微积分与矢量运算等策略。学习物理知识的过程是一个循序渐进的过程，学习上因循守旧不思进取，不及时转变思维方式以适应更高层次物理知识的学习，是学不好物理的。

因此，在高中物理的学习过程中，教师应鼓励学生接触微积分，帮助学生建立初步的矢量运算和微积分基础知识，为今后大学物理的学习打下坚实的基础。此外，大学阶段教师应引导学生从初等数学理解物理知识逐渐转变为用微积分思想理解物理学基本概念和基本规律，转变高中物理的思维模式，尽量减轻初等数学的负迁移，使学生尽快熟悉并掌握新的数学工具来探究未知世界。

致谢

感谢编辑部的老师，感谢对我文章提出宝贵意见的匿名审稿专家。

基金项目

本论文感谢国家自然科学基金(61563054)和教育部2020年高等学校大学物理课程教学研究项目(WLJG-ZN-202002)的资助。

NOTES

^*第一作者。

^#通讯作者。