1. 引言
随着基坑工程开挖深度的增大，特别是在上海等软土地区施工超深地连墙时，规范推荐的弹性抗力法已不足以得到合理的地连墙受力变形结果，并且以平面应变为前提的弹性抗力方法也无法反映大型深基坑开挖过程中显著的空间效应，导致设计与实际情况相差较大，造成不必要的风险。基于地层结构法的三维有限元数值模拟能够较好地反映深基坑工程中的空间效应，但土体本构模型的选择对模拟结果有着决定性的影响。
目前主流的本构模型包括Mohr-Coulomb (MC)模型、Druker-Prager (DP)模型、修正剑桥(MCC)模型以及近几年被广泛用于模拟基坑工程的Hardening Soil-Small小应变(HSS)模型，其中MC模型和DP模型属于理想弹塑性模型，MCC模型和HSS模型属于硬化类弹塑性模型 [1]。目前已有不少学者利用不同的模拟方法对软土地层深基坑开挖过程进行了数值模拟研究，刘杰等 [2] 利用ANSYS有限元软件建立了某地铁车站深基坑开挖二维数值计算模型，模型中土体本构模型选用了Mohr-Coulomb模型，通过与现场监测数据的对比验证了模型的可信度，并进一步对支撑位置、围护结构插入土体深度等因素对结构变形的影响进行了分析；戴斌等 [3] 利用Plaxis 2D有限元软件建立了基坑群开挖二维数值计算模型，本构模型选用能较好模拟上海典型软土地层的HS模型，研究了基坑群间缓冲区宽度对相邻基坑同步开挖的影响；陆新征等 [4] 通过ANSYS有限元软件对某深基坑开挖过程支护结构与土体的共同作用进行了三维数值模拟分析，其中土体本构模型选用Drucker-Prager模型，提出结构–土体共同作用的非线性空间效应对变形的影响；徐中华 [5] 针对上海典型软土选用了修正剑桥模型(MCC模型)作为土体本构模型，利用ABAQUS有限元软件对三个上海典型深基坑开挖施工过程进行了三维数值模拟，分析了上海地区支护结构与土体相结合的深基坑变形性状；吴瑞拓等 [6] 考虑了软土地区深基坑开挖属于小应变范围，选择了土体小应变硬化模型(HSS模型)作为土体本构模型，利用Plaxis 3D有限元软件对上海地区一典型软土地铁深基坑开挖过程进行了三维数值模拟分析，探究了深基坑开挖全过程的变形性状；张浩等 [7] 基于简化小应变模型(IGS模型)通过Plaxis 3D有限元软件建立了三维数值模型，对基坑开挖过程中领近隧道的响应进行了研究，验证了该本构模型的可行性；张娇等 [8] 采用HSS本构模型对上海世博片区绿谷一期深大基坑工程进行了三维有限元模拟分析了基坑开挖对领近隧道的影响；李靖等 [9] 采用HSS本构模型对鼎鼎外滩深基坑工程进行了模拟分析了基础换托对周边建筑物的影响；刘磊等 [10] 基于HSS模型建立了全应变范围内的非线性弹性本构模型并对台北TNEC基坑工程进行了有限元分析；宗露丹等 [11] 利用HSS本构模型并结合实验参数对上海国际金融中心深基坑工程施工过程进行了模拟分析对比了不同施工顺序对基坑变形的影响；徐中华等 [12] 基于HSS模型对上海虹杨500 kV地下变电站逆作法深基坑工程进行了模拟分析，研究了各工况下的基坑及土体变形情况；王浩然等 [13] 利用土体硬化模型对华山医院改扩建工程深基坑开挖过程进行了三维数值模拟，探究了基坑开挖对邻近建筑物及周围环境的影响。
2. 工程简介
2.1. 工程概况
上海某盾构隧道工作井由两口工作井及中间连廊组成，工作井边长25 m，连廊宽15 m、长90 m，两侧工作井埋深约36.6 m，连廊埋深约31.1~35.8 m，均采用明挖顺作法施工，基坑平面布置以及主要测点布置如图1所示。其中DB为沉降监测点，P2~7为地连墙深层水平位移监测点。
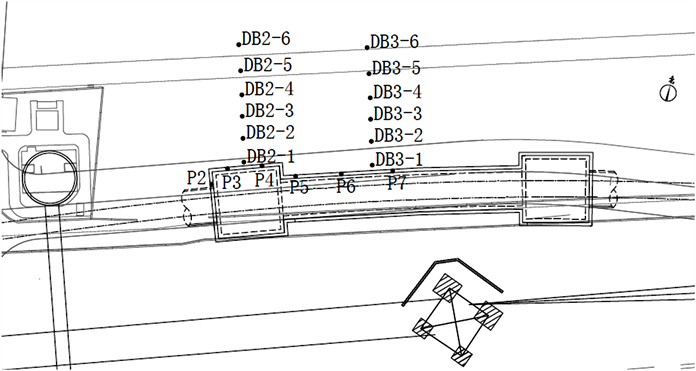
Figure 1. Layout of foundation pit and main monitoring points
图1. 基坑平面布置及主要监测点布置图
2.2. 工程地质
基坑开挖范围内主要土层情况依次为：① 填土，厚度为1.7 m；
灰黄色粉质黏土，厚度为1.3 m，可塑；
灰色淤泥质粉质黏土，厚度为6 m，流塑；④ 灰色淤泥质粉质黏土，厚度为4.5 m，流塑；
灰色粉砂夹粉质黏土，厚度为2.5 m；
灰色粉质黏土，厚度为10.5 m，软塑为主；
暗绿色粉质黏土，厚度为4.2 m，可塑；
灰黄色粉砂夹粉质黏土，厚度为6.6 m；
灰色粉细砂。
2.3. 基坑支护方案
本工程基坑支护方案为地下连续墙+支撑体系(图2)，其中围护结构采用1.2 m厚的地下连续墙，深度在两侧工作井处为66 m，连廊位置处为61 m。沿基坑开挖深度设置十道支撑，其中一、三、五、七、九道为钢筋混凝土支撑，截面面积分别为1000 mm × 1000 mm、1200 mm × 1000 mm、1400 mm × 1000 mm三种，二、四、六、八、十道为双肢钢管支撑，截面分别为∅800，t = 20 mm以及∅609，t = 16 mm两种。
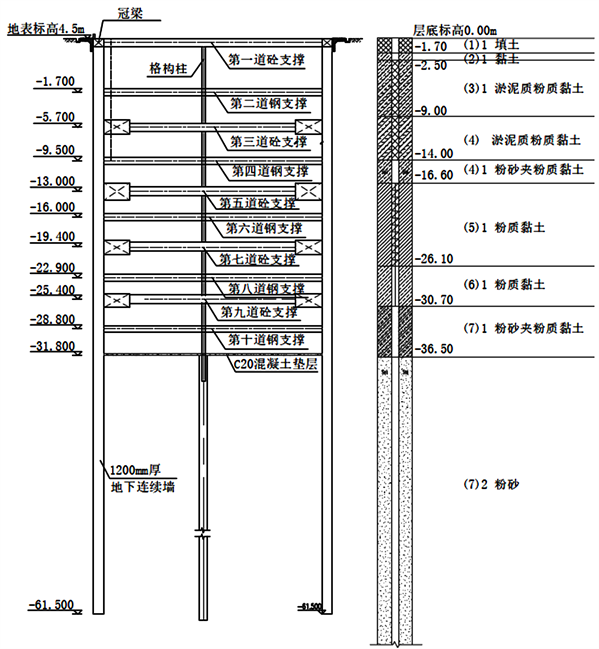
Figure 2. Sectional view of foundation pit
图2. 基坑剖面图
3. 超深地连墙施工过程三维有限元模拟
3.1. 三维数值模型
分别采用ABAQUS和Plaxis3D软件建立深基坑三维数值模型，模型中包括土体、地连墙、支撑体系(支撑、腰梁及格构柱)。其中ABAQUS中的土体模型为避免边界效应，尺寸确定为400 m × 250 m × 100 m，并沿深度方向将土体分成8层(其中将①填土与
层土共同考虑)土体本构模型采用MC模型，采用三维实体单元C3D8进行土体建模，地连墙选用壳单元S4R建模，支撑体系均用梁单元B31建模。模型中主要接触为墙体和土体绑定，支撑体系和墙体绑定，格构柱埋入土体部分为嵌入式约束，边界条件为模型四周设置法向约束，底部设置固定约束，地表自由。整个模型一共288,685个单元、305,720个结点。
而Plaxis3D中土体模型平面尺寸为400 m × 325 m，创建钻孔分割土层，埋深最大为120 m，土体本构模型选用HSS模型，采用10节点实体单元建模，地连墙采用6节点Plate板单元建模，支撑体系均选用3节点beam梁单元建模，其中格构柱埋入土体部分用embedded桩单元建模，地连墙与土体之间的接触通过界面单元模拟。整个模型一共158,422个单元、254,758个结点。三维数值模型如图3所示。
3.2. 土体模型计算参数
ABAQUS土体本构模型选用机理最明确的MC模型，其参数取值较为简单。Plaxis3D的土体本构选用HSS小应变模型，能够更准确地反映软土在深基坑开挖过程中的力学响应，但土体参数较多，缺乏系统性研究，顾晓强等 [14] 与王卫东等 [15] 通过总结大量试验数据建立了上海地区基于土体孔隙比的HSS模型主要参数经验取值，并通过多个深基坑工程验证了其合理性。所以本文HSS模型参数参考文献 [14] [15] 结合地勘报告进行取值。本构模型计算参数取值表1、表2所示。
Table 1. Mohr-Coulomb model parameters
表1. Mohr-Coulomb模型参数
注：
为土体天然重度；E为土体弹性模量，取压缩模量的2~5倍；c为土体粘聚力；
为内摩擦角。
Table 2. HS-Small model parameters
表2. HS-Small模型参数
注：
为参考切线模量；
为参考割线模量；
为加卸载模量；
为动剪切初始模量；
为有效粘聚力；
为有效内摩擦角；
为初始剪切模量70%时对应剪应变；
为加卸载泊松比；
为参考应力；
为模量应力水平相关幂指数；
为破坏比；
为静止侧压力系数。
3.3. 结构模型计算参数
三维数值模型中的所有结构模型均采用线弹性模型，钢筋混凝土材料的弹性模量取为
，钢管的弹性模量取为
，地连墙选用厚度1.2 m的板单元模拟，支撑体系均用梁单元模拟，支撑体系截面参数如表3所示。
Table 3. Support system section parameters
表3. 支撑体系截面参数
3.4. 模拟施工步骤
两个有限元软件均可以通过单元生死的方法实现地连墙施工、土体开挖以及设置对应支撑。并且在开挖土体的同时将地下水位降至开挖面。具体模拟步骤如表4所示。
4. 结果分析
4.1. 超深地连墙侧向位移
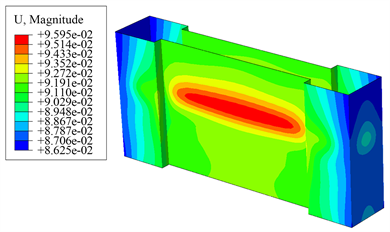
两个模型计算出的开挖至基坑底时地连墙的变形云图如图4所示。可以看出，两个计算结果都展现了地连墙变形的空间效应，变形呈现中间大两边小的鼓形，但由HSS模型计算出的地连墙最大变形位置相较于MC模型计算结果更深，最大变形量也更大。
Table 4. Simulate construction steps
表4. 模拟施工步骤
(a) ABAQUS-MC模型计算结果 
(b) Plaxis3D-HSS模型计算结果
Figure 4. Deformation diagram of diaphragm wall from excavation to the bottom of foundation pit
图4. 开挖至基坑底部地连墙变形图(单位：m)
地连墙在侧向位移监测点P2~P7位置处的模拟结果与现场监测结果对比如图5所示。可以看出实际监测结果也随着测点位置的不同呈现出空间效应，分布规律与模拟结果基本一致，其中HSS模型的地连墙侧向位移计算结果与实测值匹配度较好，地连墙位移形状呈现沿深度方向先大后小的“弓”形，且位移最大值发生在开挖面附近，经作者对大量软土地区深基坑工程的调研，该变形规律符合一般情况。主要是由于开挖过程导致地连墙内侧发生卸荷，而支撑的作用远达不到土体对结构的约束效果，所以地连墙受到外侧土体的水土压力作用，发生向内侧的位移，且按照土压力理论，外侧水土压力沿深度方向呈三角形分布，地连墙在开挖面位置处所受外侧水土压力最大，所以其位移曲线在开挖面以上沿深度方向逐渐增大并在开挖面处达到最大值，而开挖面以下土体虽然收到扰动但是仍然对地连墙有一定约束作用，且随着深度的增加，土体越密实，对结构的约束作用也越大，所以地连墙位移曲线在开挖面以下沿深度方向逐渐减小。在沿坑壁长度方向，地连墙的变形呈现较明显空间效应，这种现象称为“坑角效应” [16]，即围护结构在坑中位置的变形往往小于坑角位置，这是由于矩形基坑外侧土体在坑角位置处会受到来自坑壁两个方向的约束作用，相当于在基坑角部加了两道支撑，导致该处围护结构刚度明显大于坑中部，并且基坑长边上的地连墙侧向位移明显大于短边，可见“坑角效应”还与基坑的尺寸有关。
而相比之下MC模型地连墙的侧向位移值则小得多，这是由于HSS模型能够较好地考虑出软土在破坏前小应变范围内模量随变形而变化的规律，而MC模型在整个开挖过程中模量一直保持不变，且没有考虑应力路径，造成MC模型中土体开挖后产生较大的回弹，抵消掉了一部分地连墙的形变，这也是为什么MC模型中地连墙最大侧向位移位置较浅的原因。
而在测点P2位置处HSS模型模拟结果较现场监测值在墙顶有较大位移，这可能是由于P2位于地连墙短边上，而该部分支撑均为斜撑，相较于长边上的对撑刚度较小，并且模拟中没有考虑到浅层土体加固以及土层在不同位置的分布情况，所以造成该部分变形较大。而其他位置HSS模型的计算结果与现场监测值均匹配较好，说明采用HSS模型能够较好地反映软土地区超深地连墙开挖产生的变形。
4.2. 地表沉降
两个模型在开挖至基坑底部时的地表沉降情况如图6所示。可以看出两个模型在地表沉降的计算结果上有较大差异，MC模型在开挖基坑周围产生了明显的地表隆起，而HSS模型则在基坑周围产生了明显的沉降，并且存在空间效应。
(a) ABAQUS-MC模型计算结果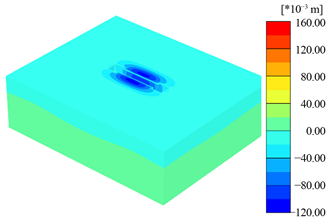 
(b) Plaxis3D-HSS模型计算结果
Figure 6. Simulation Results of Surface Subsidence
图6. 地表沉降模拟结果(单位：m)
在竖向位移监测点DB2-1~5及DB3-1~5位置处的最终地表沉降量模拟结果与现场监测结果对比如图7所示。可以明显看出MC模型中地表竖向变形表现为回弹，这不符合实际情况，说明其并不能真实反映出基坑开挖产生的地表沉降，这同样是因为MC模型过高地考虑了土体的回弹使得地表隆起。而HSS模型计算的地表沉降规律基本符合现场监测结果，地表沉降变形呈“凹槽形”，有明显的沉降槽，符合软土地区开挖土体引起的地表沉降规律，最大沉降值均发生在距离基坑10 m左右位置，地表沉降的影响范围也均在距离基坑60 m范围内，并且在空间分布上地表沉降同样存在明显的“坑角效应”，地表沉降量在坑中部明显大于坑角处，在长边上明显大于短边，说明坑壁对坑角处土体不仅有侧向约束作用还有竖向约束作用。而在基坑中部的沉降量HSS模型计算结果明显大于现场监测值，这可能是由于模拟中未考虑现场额外的土体加固措施。但可以说明相较于MC模型，HSS模型能够更真实反映出深基坑开挖产生的地表沉降情况。
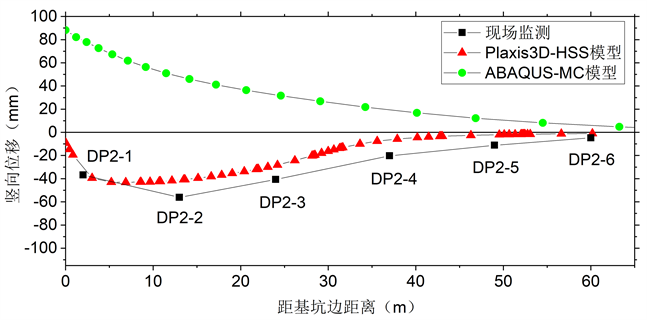
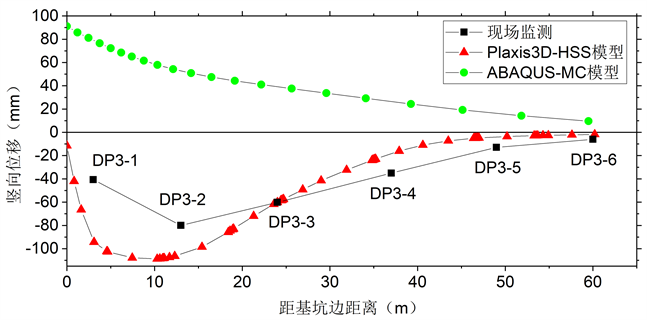
Figure 7. Comparison of calculation results of surface subsidence
图7. 地表沉降计算结果对比
5. 结论
本文以上海某盾构隧道工作井超深基坑工程为背景，通过三维有限元数值模拟方法研究了软土地区超深地连墙施工过程变形情况，并分别采用ABAQUS和Plaxis3D软件对施工过程进行了模拟，通过与现场监测结果对比探究了MC本构模型和HSS本构模型对软土地区超深地连墙施工过程变形模拟的适用性，结论如下：
1) 软土地区超深地连墙施工过程中围护结构的侧向位移以及墙后土体的地表沉降变形具有明显的空间效应，也称“坑角效应”，表现为长边较短边变形更大，中间部分较两端变形更大。
2) 软土在深基坑开挖过程的变形属于小应变范围内，所以对于超深地连墙侧向位移的模拟，HSS本构模型较MC本构模型与现场监测值更加匹配。而MC模型中坑底会产生较大的回弹导致地连墙侧向位移较小。并且MC模型无法模拟基坑开挖导致的地表沉降，而HSS模型能够更好的反映地表沉降规律，所以总体而言HSS模型能够很好地模拟软土地区超深地连墙施工过程的变形，为以后更加复杂的超深地连墙工程提供了有效分析手段。
NOTES
*通讯作者。