轴压T形分布的四肢格构柱绕非对称轴整体稳定性计算

Calculation of Overall Stability of Limb Lattice Columns with T-Shape Distribution under Axial Compression around Asymmetric Axis

摘要: 针对T形分布的方钢管四肢格构柱，对其绕非对称轴的换算长细比以及弯曲屈曲临界力计算公式进行了推导，并采用有限元软件ABAQUS对T形四肢格构柱进行有限元分析，通过对有限元模拟结果与计算公式结果进行对比，最后验证了推导换算长细比的正确性。

Abstract: For the T-shaped square steel tubular four limb lattice columns, the calculation formulas of the converted slenderness ratio around the asymmetric axis and the critical bending buckling force are derived, and the finite element analysis of the T-shaped four limb lattice columns is carried out by using the finite element software ABAQUS. The correctness of the derivation of the converted slenderness ratio is verified by comparing the finite element simulation results with the calculation formula results.

1. 引言

如今人们不再单纯的满足于建筑结构最基本的使用功能，对于房屋的美观舒适也有了更高的要求，传统的框架柱采用矩形柱，不能完全被墙体包围，柱角很大一部分突出房间内部，占用室内空间，不便于家具的布置，同时也影响建筑的美观。在这种背景下，方钢管异形柱的出现很好的解决了这一问题。

荣彬 [1] 在硕士和博士期间主要研究了L形截面方钢管混凝土组合异形柱进行轴压试验研究其破坏和发生失稳破坏的受力性能，对其长细比计算公式进行了推导，并用ANSYS验证了长细比计算公式的正确性。周婷 [2] 在硕士论文和博士论文中相继研究了L形方钢管混凝土组合异形柱的轴压性能、压弯性能及抗震性能。天津大学刘振文 [3] 为了研究方钢管混凝土组合异形柱发生强度破坏和发生失稳破坏时的承载能力，分别设计进行了关于T形短柱试件、十字形短柱试件和长柱试件的轴心受压试验。

天津大学乔景 [4] 进行了T形方钢管混凝土组合异形柱轴心受压承载力研究，提出了一套应用叠加理论的计算公式。陈志华 [5] 对于方钢管混凝土组合异形柱进行了理论计算，有限元分析和试验验证。对于方钢管混凝土组合异形柱，提出基于叠加理论的计算方法并推导了轴压力分配系数计算公式；针对L形截面(LCFT)、T形截面(TCFT)和十字形截面(XCFT)的方钢管混凝土组合异形柱，推导了等效长细比计算公式。

国内尚缺少对多肢格构式异形柱柱肢与缀件在静力和水平往复荷载作用下各自承担荷载的动态变化规律、失效机理的研究。因此，有必要研究多肢格构式异形柱的破坏机理。目前国内外研究人员只对钢管混凝土组合异形柱进行了研究，但针对工程设计及施工需要，没有关于多肢格构式异形柱相关技术条文和国家规范以及行业、地方标准的制定。因此，有必要进行多肢格构式异形柱在不同失效模式下承载力的实用计算方法及优化设计研究。

本文将推导轴压下T形分布的四肢格构柱绕非对称轴的换算长细比公式，并且通过有限元模拟软件对T形四肢格构柱进行计算分析，将有限元模拟结果与推导公式计算结果进行对比分析，验证了推导公式的准确性。

2. 构件设计

T形方钢管多肢格构柱包括肢件和缀材；肢件为方钢管a；多个肢件与多个缀材通过焊接形成异形柱；异形柱采用的缀材为方钢管b，耳板设置在异形柱顶端和底端的方钢管a侧面，通过焊接固定；一个异形柱顶端的方钢管a耳板通过螺栓与连接板一端固定，连接板另一端与另一个异形柱底端的方钢管a耳板通过螺栓连接，形成异形柱之间的对接；异形柱对接后通过焊接将顶端的方钢管a与底端的方钢管a固定连接后，切除耳板。

T形方钢管格构柱是由方钢管肢件以及方钢管缀材焊接而成，可以看作格构式构件。

图1中，1：方钢管a；2：方钢管b

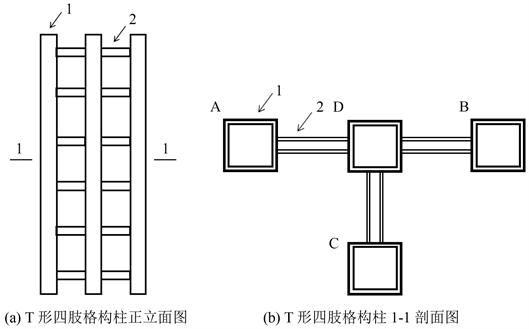
Figure 1. T-shaped four limb lattice special-shaped column

图1. T形四肢格构式异形柱

3. 长细比计算

基本假定：

1) 肢件与缀材采用刚性连接，将模型简化为刚架计算。

2) 忽略A、B柱承担的y方向剪力，CD榀刚架承担全部剪力。

3) 变形时反弯点在各节的中点。

计算T形截面方钢管异形柱时，如何确定长细比是计算的关键。由于柱肢之间通过缀板连接，而且连接两柱肢的方钢管缀板抗剪刚度较弱。所以当格构柱在承受压力作用而处于微弯平衡状态时，不但要考虑弯曲变形的影响，还要考虑缀材件剪切变形的影响。因此对于格构柱应当采用换算长细比代替原始长细比进行计算。

其格构柱绕虚轴的稳定性计算要采用经放大的等效长细比。称为格构式构件绕虚轴的换算长细比 ${\lambda }_{0x}$。根据文献 [6] 两端铰接的理想等截面格构式直柱，它的弯曲屈曲临界力为：

$N_{cr}=\frac{{\pi }^{2}EA}{{\lambda }_x^2}\times \frac{1}{1+\frac{{\pi }^{2}EA}{{\lambda }_x^2}\times {\gamma }_1}=\frac{{\pi }^{2}EA}{{\lambda }_{0x}^2}$ (1)

${\lambda }_{0x}=\sqrt{{\lambda }_x^2+{\pi }^{2}EA{\gamma }_1}$ (2)

式中N_cr——弯曲屈曲临界力；

E——钢材的弹性模量；

A——A、B柱肢的截面面积；

${\lambda }_x$ ——格构柱绕虚轴临界力的长细比；

${\lambda }_{0x}$ ——格构柱绕虚轴临界力的换算长细比；

${\gamma }_1$ ——单位剪力作用下的轴线转角。

只要求得单位剪切角 ${\gamma }_1$，即可求出 ${\lambda }_{0x}$。

下面将推导T形方钢管格构柱绕非对称轴的单位剪切角 ${\gamma }_1$。

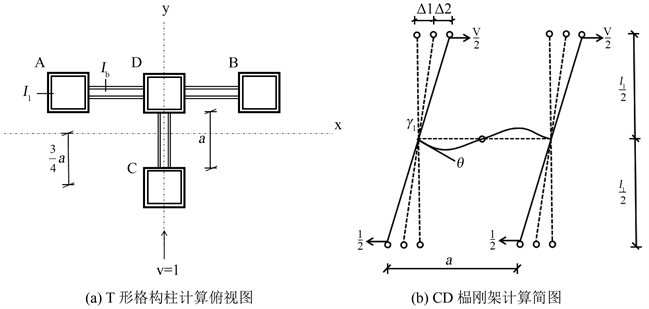
Figure 2. Calculation diagram of bending deformation of T-shaped four limb lattice column around asymmetric axis

图2. T形四肢格构柱绕非对称轴发生弯曲变形计算简图

如图2所示，当单位剪力V = 1沿主轴y轴作用时，可得缀板弯曲变形引起的分肢变位 ${\Delta }_1$ 等于

${\Delta }_1=\frac{l_1}{2}\theta =\frac{l_1}{2}\times \frac{a{l}_1}{12E{I}_b}=\frac{a{l}_1^2}{24E{I}_b}$ (3)

式中a——分肢轴线间距离；

$l_1$ ——相邻缀板中心距；

$I_b$ ——缀板的惯性矩。

分肢本身弯曲变形时的变位 ${\Delta }_2$ 等于

${\Delta }_2=\frac{l_1^3}{48E{I}_1}$ (4)

式中 $I_1$ ——一个分肢的线刚度。

可以得到单位剪切角： ${\gamma }_1$

${\gamma }_1=\frac{{\Delta }_1+{\Delta }_2}{0.5l_1}=\frac{a{l}_1}{12E{I}_b}+\frac{l_1^2}{24E{I}_1}=\frac{l_1^2}{24E{I}_1}\left(1+2\frac{I_1/l_1}{I_b/a}\right)$ (5)

把此单位剪切角 ${\gamma }_1$ 带入(2)中，并令 $K_1=I_1/l_1$， $K_b=I_b/a$，得到换算长细比 ${\lambda }_{0x}$ 为：

${\lambda }_{0x}=\sqrt{{\lambda }_x^2+\frac{{\pi }^{2}A{l}_1^2}{24I_1}\left(1+2\frac{K_1}{K_b}\right)}$ (6)

分肢截面面积 $A_1=0.5A$，令 $A_1{l}_1^2/I_1={\lambda }_1^2$，则：

${\lambda }_{0x}=\sqrt{{\lambda }_x^2+\frac{{\pi }^2}{12}\left(1+2\frac{K_1}{K_2}\right){\lambda }_1^2}$ (7)

式中 ${\lambda }_1$ 为分肢的长细比， $K_1$ 为一个分肢的线刚度， $K_b$ 为缀板线刚度之和。

4. 有限元模拟

4.1. 钢材本构关系

本模拟方钢钢管采用的是Q235钢材，钢材的应力应变关系曲线一般分为弹性段、弹塑性段、塑性段、强化段和二次塑流段，本文在abaqus中对方钢管采用理想弹塑性模型本构关系，具体钢材力学性能参数见下表1所示。

Table 1. Mechanical properties of steel

表1. 钢材力学性能参数

4.2. 单元选取与网格划分

有限元建模中，肢件与缀材方钢管采用实体单元模拟，保证计算精度。网格划分对结果影响显著，经过多次试算对比，网格尺寸确定为：肢件方钢管网格尺寸100 mm、缀材方钢管网格尺寸为80 mm。

4.3. 边界条件及荷载的施加

在建立有限元模型和设置接触单元参数完成后，对有限元模型进行加载求解。

静力分析：约束T形四肢格构柱底面节点的所有平动自由度(x，y，z方向)和柱顶面节点的(x，y向)的平动自由度，使柱子处于两端铰结约束状态。将柱顶面所有节点z向平动自由度耦合，见下图3所示，以保证在加载过程中柱子始终保持轴心受压状态。在柱顶面耦合节点中的主自由度(耦合节点中，编号T35节点的z向自由度)节点上施加单位压力。

Figure 3. Z-direction translational degree of freedom coupling

图3. Z向平动自由度耦合

本模拟将格构柱加载面耦合于一点RP-11，使得格构柱四肢受力截面耦合约束，确保加载点保持一致，并保证模拟采用轴心受压方式进行加载。进而固定两端约束，使其成为全刚接接触形式，并且给予耦合RP-11加载点Z轴方向−40 mm位移进行加载。具体情况如图4所示。

4.4. 计算模型参数

T形方钢管四肢格构柱高3.3 m。方钢管截面尺寸为150 mm × 150 mm，管壁厚为5 mm；缀材方钢管截面尺寸为50 mm × 50 mm，管壁厚为2.5 mm，缀材方钢管长225 mm，相邻缀材中心距为550 mm；肢件和缀材均采用Q235钢材，fy = 235 MPa。

5. 结果分析

5.1. 有限元模拟以及公式计算结果

有限元分析得到的荷载–位移曲线如图4所示，破坏变形如图5所示。通过读取荷载–位移曲线上的最大值 ,可以得到当位移达到2.82 mm时，T形方钢管四肢格构柱达到弯曲屈曲临界力，计算模型得到的极限承载力为1270.03 kn，并且可以确定破坏形式为弯曲屈曲。按照本文计算公式对模型进行计算，得到的极限承载力为1216.52 kn，将结果汇集，对比结果如表2所示，有限元模拟结果偏大，误差为4.4%，且破坏形式均为弯曲屈曲。可以得到结论有限元分析结果与理论计算结果两者较吻合。

Figure 4. Load displacement curve of szg-1 four limb lattice column

图4. SZG-1四肢格构柱荷载–位移曲线

(a) 弯曲变形主视图 (b) 弯曲变形左视图 (c) 弯曲变形俯视图

Figure 5. Bending deformation of T-shaped four limb lattice column

图5. T形四肢格构柱发生弯曲变形

5.2. 结果汇总

为了保证结果具有精确性，本课题共选用8个T形四肢格构柱模型进行公式推导计算以及有限元模拟计算，有限元分析得到的荷载–位移曲线如图6所示，并将两者结果进行汇总对比，汇总对比结果如表2所示。

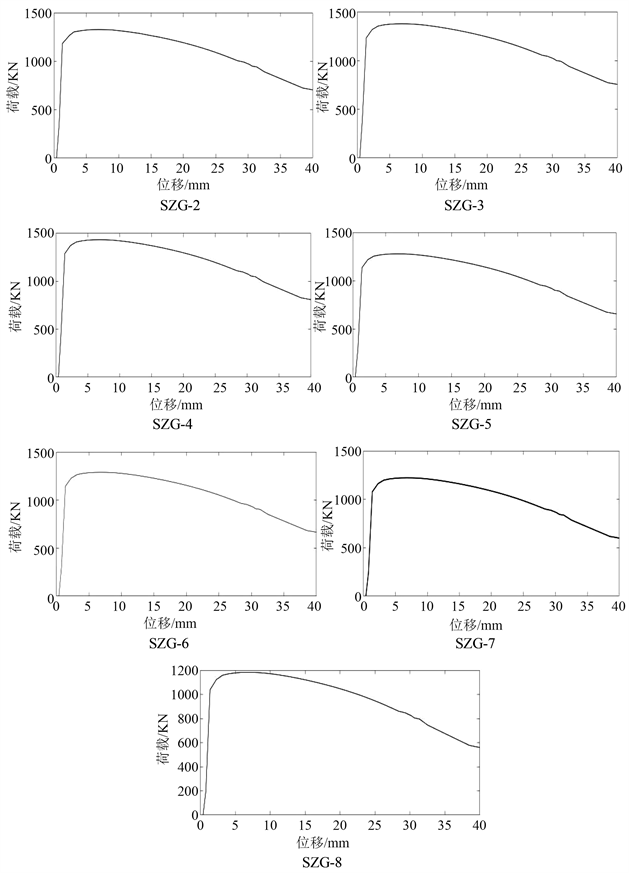
Figure 6. 2-8 load displacement curve of T-shaped four limb lattice column specimen model

图6. 2-8 T形四肢格构柱试件模型荷载–位移曲线

Table 2. Comparison and analysis of finite element simulation and formula calculation results

表2. 有限元模拟与公式计算结果对比

通过分析表2模拟汇总结果可以得出，随着肢件以及缀材尺寸的不断增大，T形方钢管四肢格构柱的极限承载力也在不断升高，并且极限承载力的模拟结果与本文公式计算结果相比，误差保持在5%以内，有限元分析结果与理论计算结果两者较吻合，验证了本文推导的换算长细比计算公式正确性。

6. 结论

1) 由理论分析以及模拟计算结果可知，T形方钢管多肢格构柱这种新型结构具有良好的承载力。

2) 本文对T形分布的四肢方钢管格构柱绕非对称轴异形柱的换算长细比计算公式进行了推导，并结合有限元软件分析进行了验证。通过对比可知，理论分析与有限元分析的结果吻合较好，验证了换算长细比计算公式的正确性。

通过本文推导公式可以初步得出，分肢、缀板线刚度会对T形四肢格构柱稳定承载力产生影响，并且可以通过有限元模拟进行参数化分析工作。