1. 引言
自升式钻井平台是海洋工程领域最重要的设备机械之一,因其有着安装便利性和经济效益高的特点而被广泛应用于近海勘探油气资源等重大海洋项目。海洋里的海床地基常有上硬下软的土层结构,桩靴基础易发生突然穿透上层硬土层进入下卧软弱层的穿刺破坏,严重时会造成整个上层平台的倒塌或者倾覆失稳 [1]。传统型桩靴基础截面形状为纺锤型,筒型桩靴由于承载力强,在穿刺破坏上有更优的表现,近年来受到了更多的关注和研究。同时一些新型的桩靴基础形式被设计出来去解决工程安装的问题,所以对于不同新型的桩靴基础在贯入过程中的影响情况进行研究有重要意义 [2]。
吴曲楠等 [3] 采用CEL方法建立有限元模型,对比模型试验和数值模拟数据,研究了筒型桩靴在贯入过程的速度和阻力影响;Hossain等 [4] 通过一系列离心机试验,并和大变形有限元分析模拟对比,表明筒型桩靴减少了有效砂层的厚度,显著减轻了穿刺破坏风险;周龙等 [5] 用CEL模拟分析桩靴在连续贯入时的速度响应和临近桩影响。陈昌哲等 [6] 对3种桩靴原型在不同水深下的水动力影响情况进行数值分析。本文研究内容可为自升式钻进平台的桩靴桩腿安装工程提供新的参考方案。
2. 筒型桩靴基础贯入过程的仿真模拟
2.1. CEL模拟方法
对于基础贯入问题的研究,实际工程中贯入桩靴基础是一个动态连续过程,海底的地基在自升式钻井平台连续的荷载作用下产生塑性破坏。桩靴基础的贯入模拟是大变形过程,因此本文采用耦合欧拉-拉格朗日方法CEL (Coupled Eulerian-Lagrangian)进行三维有限元分析 [7]。在CEL方法中,土体为欧拉体,欧拉法认为空间和材料是离散的,计算过程中网格单元的形状、大小位置保持不变,允许材料在其中流动通过 [8]。桩靴基础结构为拉格朗日体,拉格朗日法认为材料和网格呈绑定状态,这样能准确的得到桩靴结构应力应变的反馈响应。因此CEL方法适用于流固耦合和大变形的仿真,可以很好地拟合本试验桩靴基础贯入的过程。欧拉材料体积分数EVF (Eulerian Volume Faction)可以用来控制计算欧拉材料被填充的程度,EVF = 1表示材料完全填充,EVF = 0表示网格内无材料填充。
2.2. 桩靴基础及土体模型
本试验中,地基区域和多种桩靴基础的有限元模型见图1所示。地基土体为深蓝色的长方体区域,划分为两部分,图1中上层为预留空腔,允许土体材料流动被挤出到上层,EVF = 0,下层为土体区域,EVF = 1。为消除边界效应影响,地基长、宽的尺寸为6倍桩靴直径,深度为6倍桩靴高度。

Figure 1. Foundation soils and three spudcan finite element models
图1. 地基土体和3种桩靴基础有限元模型
图1中展示了3种桩靴基础形式的网格划分图,其中图1(a)为新型多筒桩靴、图1(b)为单筒型桩靴、图1(c)为传统型桩靴,每个桩靴模型设置参考点RP (Reference Point)在顶部连接桩腿的圆柱体圆心处,通过创建约束使桩靴基础整体被视为刚体,桩靴基础被放置在两层土体欧拉体的中心位置,初始位置为桩靴基础圆盘底面刚好接触下层土体,同时通过对参考点RP施加位移来模拟贯入过程,贯入总深度为2倍桩靴直径。
2.3. 数值合理性验证
本次有限元模拟试验的工况主要对于3种形式的桩靴基础在贯入过程中的表现进行横向对比,为验证数值参数准确性,选取模型与实际尺寸比1:500的多筒型桩靴基础,进行竖直贯入砂土试验,将模型试验与数值模拟的贯入阻力结果对比,在其他加载条件相同的情况下,在贯入深度为0~1倍桩靴直径时,贯入阻力平均偏差值为13%,无量纲化数据结果吻合较好。此时土体模型参数类型为砂质粉土,具体的参数取值见表1。
2.4. 模拟桩靴贯入过程
本有限元分析的3种形式桩靴基础模型主体尺寸大致相同,尺寸标注见图2。需要指出,贯入深度d统一位置在最大直径底端,3种形式有着相同的桩靴最大直径D、最大直径底部至桩靴底端距离h。新型多筒桩靴基础的小筒结构有4个,小筒直径为D0。
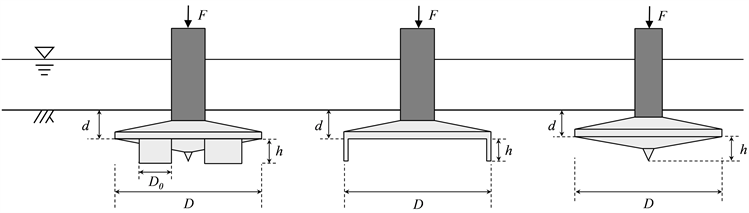
Figure 2. Three spudcan penetration schematics
图2. 3种桩靴基础贯入示意图
3. 数值模拟计算分析
3.1. 贯入阻力分析
自升式钻井平台需要通过贯入桩靴至海底来提供所需承载力且在寿命期间经常需要重新变更地址,因此插桩过程中桩靴基础收到土体传导的竖向贯入阻力是关键的工程因素 [9]。在分析不同形式桩靴基础贯入过程时,计算相同工况下插桩的竖向贯入阻力,所得新型多筒桩靴、单筒桩靴和传统型桩靴的竖向贯入阻力V随贯入深度d/D的变化情况如图3。

Figure 3. Spudcan penetration resistance curve
图3. 桩靴基础贯入阻力曲线
从图3可看出,3种不同形式桩靴基础的竖向贯入阻力V均随相对贯入深度呈增加趋势,3种桩靴基础在贯入深度为0.6倍桩靴直径时的竖向贯入阻力相差不大,其中单筒型桩靴在贯入更深深度时承载力大大超过传统型桩靴基础,新型多筒桩靴略高于传统型桩靴,在2倍桩靴直径贯入深度时,单筒型桩靴的竖向贯入阻力V为传统型桩靴的1.89倍,意味着单筒型桩靴的承载力有很大优势。同时可以看出,新型多筒桩靴的承载力变化平均浮动情况要小于传统型桩靴和单筒型桩靴,表明新型多筒桩靴在贯入时传导的承载力有更加稳定的特点。
3.2. 土体变形位移矢量
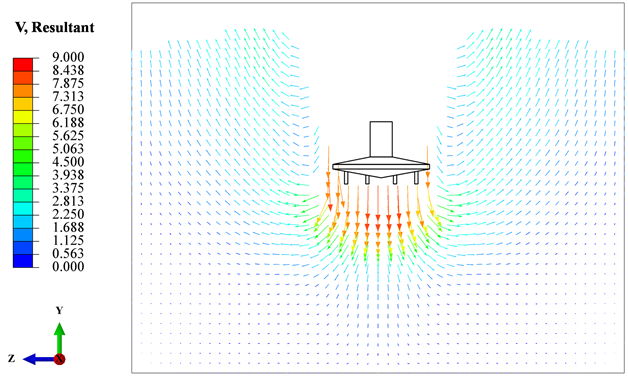
工程中海洋地质较复杂,对贯入时的桩靴附近土体位移变形情况的研究有很高重要性,选取贯入过程中贯入深度为1倍桩靴直径时的中心纵剖面土体位移情况进行分析,土体位移矢量图见图3。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 4. Vector map of soil position displacement during spudcan penetration
图4. 桩靴基础贯入过程土体位移矢量图
从图4中可看出桩靴基础下方土体位移均有集中,并向下方和两侧传递,甚至形成部分环形流动回到土体上层。关注桩靴基础下方位移速度大小,可发现土体位移聚集程度单筒型桩靴和新型多筒桩靴要大于传统型桩靴。其中单筒型和新型多筒由于下方的筒型结构形成了更多土塞区域,土塞随着桩靴基础一同向下运动,因而产生了土体位移的集中。而传统型桩靴则主要将土体向下方的两侧排开,使土体位移的速度聚集更快的消散且没有形成规模的土塞效应。
根据桩靴贯入时的破坏理论,常规破坏模式主要指桩靴将下方土体排开到两侧,而土塞破坏模式是指砂土层直接发生垂直剪切破坏,未排向两侧。两种模式的贯入阻力变化不同,土塞破坏会在同一深度下有更高的阻力和承载力表现。在贯入时的土体位移矢量图结果来看,新型多筒桩靴和单筒桩靴在贯入过程中有明显的土塞破坏倾向,且能提供更高的承载力。
3.3. 等效塑性应变
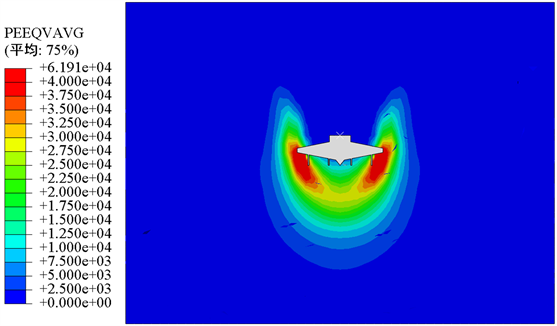
海底地基在贯入的连续荷载作用下产生塑性破坏,有限元模拟中PEEQ是表示土体内部已经产生的等效塑性应变,用来判断桩靴贯入过程中产生的土体扰动和破坏范围。图5为本文3个研究桩靴模型对象在相同贯入深度时周围土体的等效塑性云图 [10]。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 5. The equivalent plastic contours of soil
图5. 等效塑性应变云图
图5(a)新型多筒桩靴和图5(b)单筒型桩靴的土体扰动范围要略大于图5(c)的传统型桩靴。由图可知在桩靴周围水平方向上,3种桩靴基础的土体影响范围相差不大,贯入1倍桩靴直径深度时,影响宽度均约为桩靴最大直径的1.86倍;但是在竖直方向上挤压效应明显,新型多筒桩靴和单筒型桩靴要大于传统型桩靴,新型多筒桩靴影响深度约为传统型的1.43倍,单筒型桩靴约为传统型的1.85倍。同时最大塑性应变(深红颜色)处均在桩靴四周边缘,新型多筒桩靴和传统型桩靴挤压土体方向与水平面呈一定角度,与桩靴基础水平面形成较稳定三角形,而单筒型桩靴则沿单筒筒壁垂直向下,所以新型多筒桩靴在增大影响土体范围基础上保留了部分传统型桩靴基础的特点。
4. 结论
为探究自升式海洋钻井平台安装时的桩靴基础结构形式的影响,本文用CEL动态模拟方法对3种不同形式的桩靴基础在贯入海底地基的过程进行模拟,结果表明:
1) 3种形式桩靴基础的竖向贯入阻力V均随相对贯入深度呈增加趋势,2倍桩靴直径深度时单筒型桩靴的承载力为传统型桩靴的1.89倍,新型多筒桩靴基础的承载力略高于传统型且更稳定。
2) 贯入过程中桩靴基础周围土体位移下方和两侧传递,其中单筒型和新型多筒由于下方的筒型结构形成了更多土塞区域产生了大于传统型桩靴的土体位移竖向集中,有更优的工程理论表现。
3) 等效塑性应变云图表明3种桩靴基础在水平方向上的土体影响范围相似,均约为桩靴直径1.86倍,但在竖直方向上新型多筒桩靴和单筒型桩靴挤压效应明显;同时最大塑性应变处均在桩靴四周边缘,新型多筒桩靴在增大影响土体范围基础上有与传统型桩靴基础相似的挤压土体方向角度。