结构型式对高速制动盘流场及温度场影响分析

Influence of Structure Type on Flow Field and Temperature Field of Brake Disc for High-Speed Train

摘要: 为研究高速列车紧急制动工况下制动盘结构型式对于制动盘空气阻力以及散热性能的影响，通过建立轮盘轴盘以及附近空气流场的有限元模型，基于ANSYS Fluent流固耦合仿真方法，得到结果包括轴盘及轮盘温升、空气阻力及散热功率变化规律，研究结果表明，轴盘相较于轮盘具有更优越的性能。

Abstract: To study the influence of disc structure type for air resistance and heat dissipation performance during high-speed train emergency braking, the finite element models including wheel-mounted brake disc, axle-mounted brake disc and related air flow field were put forward. The conclusions about the temperature rise, air resistance and thermal dissipation were obtained based on ANSYS Fluent flow-solid conjugation simulation method. Finally, it is detected from result that axle-mounted brake disc has better performance than the wheel-mounted brake disc.

1. 引言

任何载运交通工具都绕不开制动的问题，尤其对于高速列车，如何将列车庞大的能量消耗并使列车安全平稳制动一直是制动系统设计者关注的焦点问题之一。随着社会的发展，制动系统的种类也越发多样，如电阻制动、磁轨制动、涡流制动等 [1]，然而盘形制动由于其良好的摩擦性能，且制动距离短、方便维护等特性，仍然是高速列车安全制动的首选 [2]。高速列车制动过程中，制动盘通过摩擦副摩擦生热的方式，将列车高速运行时庞大的动能转化为热能，实现能量的安全转移 [3]。目前广泛应用的制动盘包括通风式制动盘及非通风式制动盘两种，然而随着列车动能的增加，制动过程中产生的摩擦热急剧增加，从而产生热应力，进而产生热斑和热裂纹等缺陷，致使制动盘失效 [4] [5]。因此为了增加制动盘的散热性能，通风式制动盘设计有由肋板等组成的散热筋结构，加强制动盘的散热能力，对于制动盘散热筋结构设计，已经有学者进行相关研究 [6] [7]。

在制动工况下期望制动盘具有优越的通风性能以带走更多的热量，而非制动工况时制动盘的通风现象会引起空气阻力，消耗牵引功率。而在制动过程中，轮盘和轴盘由于其不同的安装位置会产生不同的空气流场，这既会使制动盘本身所受到的空气制动力产生差别，同时也会影响制动盘本身的散热性能。目前已有学者对高速列车制动工况及非制动工况下制动盘流场及温度场进行研究 [8] [9] [10] [11]，然而目前的研究大多是针对单个制动盘或者轴盘，对于轮盘的流场及温度场研究甚少 [12] [13]。

本文基于ANSYS Fluent流场仿真软件，针对轴盘轮盘及周围空气流场建立有限元模型，模拟真实制动工况，采用热流密度法简化制动过程中闸瓦与制动盘之间复杂的摩擦过程，从而将问题转化为流固耦合传热问题，计算得到轴盘及轮盘温升、空气阻力及散热功率变化规律，经过对比分析得出结论。

2. 模型建立

2.1. 几何模型

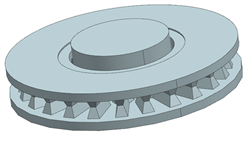
Figure 1. 3D model of axle-mounted brake disc

图1. 轴盘三维模型

以典型的叶片型散热筋结构制动盘作为研究对象，通过NX建立制动盘三维模型，轴盘模型及其散热筋结构如图1所示，轮盘模型及其散热筋结构如图2所示，在设计轮盘模型时，忽略轮缘的影响，以便于用对称结构简化轮盘模型，减少生成网格数量以及减少运算时间。

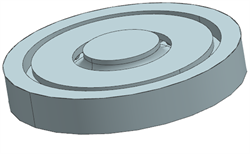
Figure 2. 3D model of wheel-mounted brake disc

图2. 轮盘三维模型

制动盘尺寸参数如表1。

Table 1. Brake disc dimension parameters

表1. 制动盘尺寸参数

流场计算域尺寸如表2。

Table 2. Flow field dimension parameters

表2. 流场域尺寸参数

2.2. 网格划分

基于ANSYS ICEM软件对三明治模型及空气流场进行网格划分，采用三角形–四面体非结构网格，在摩擦环及散热筋表面分别生成总厚度为0.2 mm及0.1 mm、增长率为1.2的6层边界层，约束三角形网格大小在1~256 mm之间，网格数量在600万左右，网格质量均大于0.25。图3所示为流场计算域全局网格，图4为制动盘表面网格。

Figure 3. Global mesh construction

图3. 全局网格

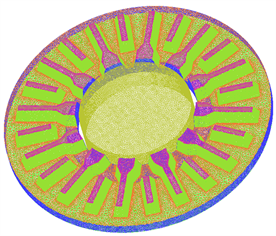
Figure 4. Mesh construction of brake disc

图4. 制动盘表面网格

3. 边界条件

在流固耦合数值分析中，需要定义的参数包括空气物理参数、固体材料参数、端面设置、模型进口风速、制动盘旋转速度、制动盘热流密度等，并根据计算工况，选择合适的Fluent计算模型及求算法。

3.1. 材料参数

计算采用标准大气参数作为流场介质的物理参数，其比热容为1006.43 J/(kg∙K)，密度为1.225 kg/m³，粘度为1.7894e−5 kg/(m∙s)，导热系数为0.0242 W/(m∙K)。制动盘为铸钢材料，其密度为7980 kg/m³比热容为489.9 J/(kg∙K)，导热系数为30.9 W/(m∙K)。

3.2. 端面设置

基于ANSYS FLUENT软件流固耦合方法进行仿真。在端面的处理上，将计算域边界设置为对称平面(symmetry)；计算域入口设置为速度入口，初始速度为400 km/h，减速度为1 m/s²；计算域出口设置为压力出口，其值为0；固体模型旋转角速度其值等于入口速度与车轮半径之比，模拟制动盘旋转；固体模型表面均为无滑移固壁边界。速度入口及压力出口的边界湍流强度为5%，湍流尺度为0.0448 m。

3.3. 热流输入

制动过程中制动盘与闸片产生的摩擦热会导致温度上升。确定摩擦面上的摩擦热流密度需要两步。第一步确定摩擦面上产生的总的热量，第二步是确定热量分别有多少流入到制动盘和闸片。制动过程中制动盘摩擦副上产生的总的热流密度如下：

$q_{total}=\frac{\eta ma\left(v_0-at\right)}{2\text{π}\left(r_{out}^2-r_{in}^2\right)}$

式中， $q_{total}$ 为总的热流密度， $\eta$ 为车体动能转化为热能的效率， $m$ 为轴重， $a$ 为制动减速度， $v_0$ 为制动初速度， $t$ 为制动时刻， $r_{in}$ 和 $r_{out}$ 分别为制动摩擦圆环的内外半径。

流入制动盘的热流密度如下：

$q_d=\beta q_{total}$

式中 $\beta$ 为热流分配系数，可用制动盘和闸片的材料参数来衡量：

$\beta =\frac{\sqrt{{\rho }_d{c}_d{\lambda }_d}}{\sqrt{{\rho }_p{c}_p{\lambda }_p}+\sqrt{{\rho }_d{c}_d{\lambda }_d}}$

式中 ${\rho }_d,{\rho }_p,c_d,c_p,{\lambda }_d,{\lambda }_p$ 分别为制动盘和闸片的密度，比热容和导热系数。固体与流体的初始温度均设置为300 K。

4. 计算结果分析

4.1. 泵风功率

轮盘及轴盘泵风功率随制动过程发展的变化规律如图5所示。

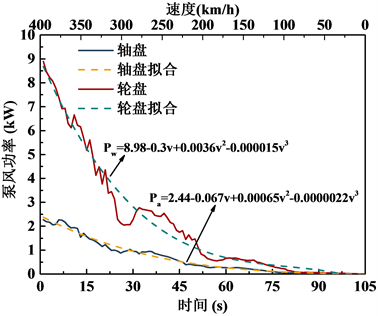
Figure 5. Air-pumping power at different times

图5. 泵风功率时间历程

其中泵风功率的计算公式如下：

$N=Fv$

式中， $N$ 为泵风功率，W； $F$ 为阻力，N； $v$ 为速度，m/s。

轮盘及轴盘所受泵风功率拟合式为：

轮盘： $P_W=8.98-0.3v+0.0036v^2-0.000015v^3$

轴盘： $P_a=2.44-0.067v+0.00065v^2-0.0000022v^3$

可以看出，制动过程开始时，阻力快速下降，随着制动的进行，阻力及泵风功率下降的趋势趋于平缓，呈现抛物线形式，这是由于模型收受的空气阻力与速度的二次方成正比关系，因此泵风功率与速度成三次方关系。

图6为轮盘流场流线图，可以看出，由于制动盘旋转与车轮结构的阻碍，使得气流在制动盘与辐板之间产生了气流涡旋，涡的耗散会引起阻力的增加。

Figure 6. Stream line of wheel-mounted brake disc

图6. 轮盘流线图

图7给出了轮盘近轮辋一侧流场压力分布情况。高速气流流到车轮前部时，由于车轮的阻挡(如图6所示)，气流不能顺利流入制动盘前端，在车轮轮辋内部面向来流一侧区域形成了较大的负压区，致使压差阻力增大。因此轮盘阻力矩大于轴盘。

Figure 7. Pressure near rim of wheel-mounted brake disc

图7. 轮盘近轮辋面压力图

4.2. 温度

摩擦面最高温度出现在65 s左右，如图8所示。

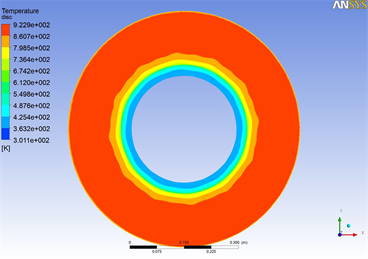(a) 轴盘 (b) 轮盘

Figure 8. Maximum temperature of friction surface

图8. 摩擦面最高温度

图9给出了制动过程中摩擦面、内侧面及散热筋表面温度随时间变化历程，可以看出，随着制动的进行，摩擦面温度先急剧上升后缓慢下降，而内侧面及散热筋的温度随时间缓慢上升。在制动初期，由于列车速度高，产生的热流密度大，并且相对于进入摩擦面的热量，由于制动盘材料热传导性能的限制，热传导流入制动盘内部及热对流散失的热量少，导致摩擦面温度的急剧升高；而随着制动的进行，列车的速度降低，热流输入变小，同时更多的热量通过热传导流入制动盘内部，制动盘散热筋逐渐发挥其散热能力，表现为摩擦面温度缓慢上升直至下降，散热筋温度表现为逐渐上升趋势。

对比轴盘及轮盘的温度变化可以看出，轮盘的最高温度大于轴盘，轮盘最高温度为637.66℃，轴盘为609.14℃，并且在单次的制动过程中，散热筋的温升不明显。

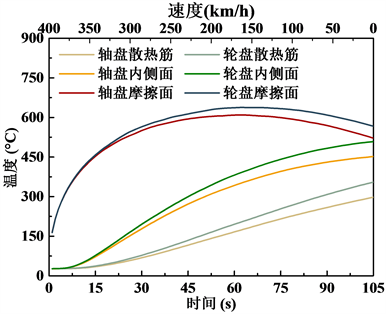
Figure 9. Temperature at different times

图9. 温度时间历程

4.3. 散热功率

图10给出了轮盘及轴盘制动过程中各个部分散热功率的变化规律。从中可以得出，对于制动盘整体，其散热功率先上升后下降，呈抛物线形式，结合图9，制动初始阶段虽然速度高，对流换热能力强，但是由于温度较低，整体的散热功率低，随着时间的发展，散热功率逐渐上升，之后由于列车速度降低，对流换热能力下降，导致最终散热功率的减小。对于轴盘及轮盘，其散热功率并没有明显区别。

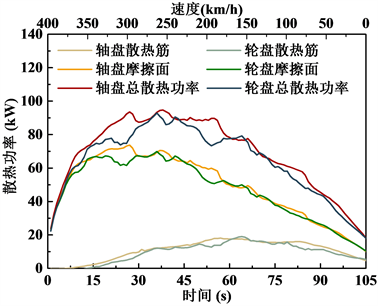
Figure 10. Heat dissipation power at different times

图10. 散热功率时间历程

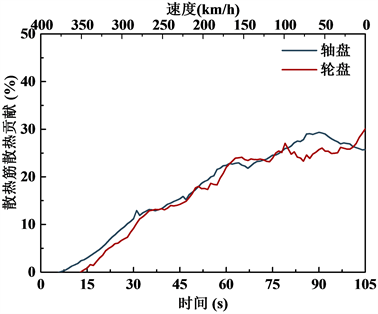
Figure 11. Ratio of rib heat dissipation at different time

图11. 散热筋散热贡献时间历程

如图11，可以看出在制动过程中，摩擦面散热占主导地位，散热筋散热的占比不大，在制动过程末段逐渐发挥功效。

定义泵风–散热效率比，其表达式为：

${\eta }_v=\frac{Q_{areo}}{Q_{con}}$

式中， ${\eta }_v$ 为效率比， $Q_{areo}$ 为泵风功率， $Q_{con}$ 为散热功率。对于不同结构的制动盘模型，我们希望其泵风功率尽可能小，散热功率尽可能大。

图12为轮盘轴盘效率比，可以看出轴盘相较于轮盘从泵风功率及散热性能方面有更优越的性能。

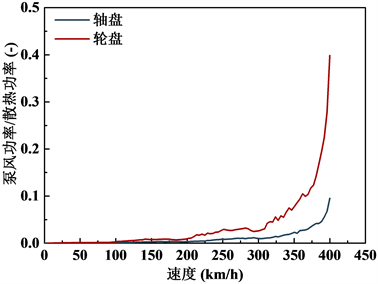
Figure 12. Air-pumping efficiency ratio at different velocity

图12. 不同速度的泵风效率比

5. 结论

基于ANSYS Fluent流固耦合研究制动盘安装位置对制动盘泵风功率及散热功率的影响，能得出以下结论：

1) 制动过程中，泵风功率随时间逐渐降低，与速度的三次方成正比，轮盘的泵风功率高于轴盘；

2) 制动过程中摩擦面温度最高值不在制动结束阶段，而是呈现先上升后下降的趋势，且制动盘散热筋温度随时间的发展一直升高，整个制动过程中，轮盘的温度大于轴盘；

3) 整体散热功率先上升后下降，呈抛物线形式，并且摩擦面散热在其中占主导地位，散热筋结构散热效率不高，并且轮盘与轴盘散热功率大致相当。从泵风散热比的角度综合考虑轮盘与轴盘的泵风损耗与散热效率，轴盘较轮盘有更优越的性能。