1. 引言
随着日本学者Koizumi等 [1] 为提高材料在热荷载作用下的性能首次提出功能梯度材料,该种材料的材料组成成分可以产生连续变化,材料性能也可以根据需求呈现梯度变化 [2]。功能梯度材料首先应用在了航空航天领域以及核反应领域 [3],之后各领域也相继引入了功能梯度材料。在土木工程领域,功能梯度材料也有着极大的优势,在工程环境严峻的地段引入功能梯度材料将大大减少施工难度以及节省施工材料。目前,土木工程领域对于功能梯度材料仍处于理论与实验阶段,大多数通过假设以及理论分析建立衬砌结构的理论模型。圆筒作为一种典型的具有轴对称特征的工程结构,在航天、机械、石油天然气、隧道等工程领域具有广泛的应用。一些学者将功能梯度概念引入圆筒结构并进行了深入的研究。
本文将基于功能梯度圆筒结构的力学特性理论研究、功能梯度立井井壁、功能梯度地铁隧道衬砌结构及功能梯度圆筒结构制备方法进行一定总结与分析。
2. 功能梯度圆筒的力学特性研究
目前,许多国内外学者的研究大多以Mises或Tresca屈服准则为前提,假设圆筒的弹性模量或泊松比满足某一函数分布,采用弹性力学理论或复变函数求解不同荷载情况下功能梯度空心圆筒内部的应力和位移的解析解。目前大多数研究都将泊松比作为常数,假设泊松比变化对结构的应力和位移影响较小,从而简化圆筒复杂平衡方程的求解计算。Nie等 [4] 的结果表明当圆简厚度不太大时,泊松比的变化对结构应力和位移的影响微弱,但是与Li和Peng [5] 发现随着圆筒的厚度变大,泊松比的影响越来越不容忽视。现有研究中假设的功能梯度圆筒中的弹性模量函数,根据函数中含有的材料参数数量可分为:双参数假设和三参数假设。根据函数形式又可分为:幂函数、指数函数、线性函数以及三角函数等。
2.1. 双参数假设
在线性函数的假设中,Shi和Xiang [6] [7] 研究了具有连续梯度材料性能的弹性空心圆柱体,材料泊松比为常数,弹性模量关于半径以线性函数式(1)变化,采用位移法求解了Whittaker方程和超几何方程,与以拉梅解答和递推算法为基础确定的多层圆柱在内外表面均布压力作用下相邻两层间挤压应力的精确解吻合较好。
(1)
在幂函数的假设中,许多学者常常假设材料的泊松比为常数,弹性模量为关于半径r的幂函数,使用不同的求解方法进行研究。如Yang [8] 主要通过假定材料泊松比为常数,弹性模量为关于半径r的幂函数式(2),从而得出FGM热应力的解析解,此解对弹性材料为精确解,对有蠕变行为材料则为渐近的解;Horgan和Chan [9] 假设材料泊松比为常数,弹性模量为关于半径r的幂函数式(3),通过改变函数中n值,使材料非均匀性变化,得出n与径向距离之间的关系,从而得出圆筒在外压下存在应力屏蔽效应的n值范围;宋日新 [10] 假设功能梯度圆筒的弹性模量为关于半径r变化的幂函数式(3),通过调整两种材料体积分数的方法实现圆筒功能梯度变化,借助超几何级数求得功能梯度圆筒受内压的弹性理论解,并且利用ANASYS建立分层圆筒模型验证了解析解的正确性;Tutuncu和Ozturk [11] 假定功能梯度材料泊松比为常数,弹性模量为关于半径r的幂函数式(4),使用无穷小的弹性理论得到了功能梯度柱形容器在内压力作用下应力和位移的闭式解,并且分析了材料的弹性模量变化对壳内应力的影响规律。也有学者通过研究弹性模量沿环向方向发生变化,假设弹性模量随角度的变化而改变。如张通通等 [12] 假定功能梯度圆筒的弹性模量沿环向方向发生改变,设置结构弹性模量为关于角度的n次幂函数式(5),建立了功能梯度深埋地铁隧道衬砌的圆筒模型。除了研究圆筒结构中材料弹性模量梯度改变,一些学者也对材料的其他参数开展了研究。如Batra [13] 假定材料泊松比为常数,剪切模量沿半径方向以幂函数式(6)变化,对线弹性不可压缩的功能梯度圆筒进行了变形分析,推导了内外加压无限长圆柱形空腔的空间解,得出在圆柱体中环向应力或周向应力的最佳值是一个常数,并且在径向上呈线性变化的结论。
(2)
(3)
(4)
(5)
(6)
在指数函数的假设中,学者们主要还是研究材料弹性模量随着半径r变化的关系。如You [14] 等用指数函数式(7)来描述中间功能梯度层的弹性模量,得到一种收敛速度快、精度高的适用于内压作用下功能梯度材料制厚壁球形压力容器的分析方法;Sburlati [15] 假设弹性模量沿半径方向呈幂函数和指数函数式(8)并且发生连续变化,得到内外压力作用下厚壁圆筒的解析解,显示了不同剖面材料梯度特性对应力场和位移场的影响;Chen和Lin [16] 通过假设弹性模量沿半径方向为指数函数形式式(9),提出了一种有效计算介质应力分布的数值方法,研究了沿径向的应力分布,并得出纤维梯度材料的性能对径向应力分布有显著影响的结果。
(7)
(8)
(9)
2.2. 多参数假设
对于某些功能梯度圆柱,需要满足内外侧弹性模量为一个特殊值,即固定内外边界的弹性模量。采用两参数假设,中间梯度层的弹性模量只能沿固定规律变化,很难使梯度层任意变化以满足实际需要。为了解决这一问题,部分学者在两个参数的基础上提出了三个或者多个变量参数来表示圆柱内的弹性模量,从而使中间区域的弹性模量可以根据各种梯度规律变化。
对于多参数假设,大多数学者主要是通过建立多项式函数来控制径向弹性模量的变化,其中Chen和Lin [17] 假设圆筒中材料弹性模量为二次函数式(10)通过控制内外层的弹性模量为固定值,中间梯度层弹性模量按着假设规律变化,研究功能梯度圆筒的特性,弹性模量变化如图1所示。Durodola和Attia [18] 分别假设弹性模量为n次函数式(11)、二次函数式(12)变化的函数形式,见图2,进行功能梯度圆筒模型的研究。Eraslan和Akis [19] 假设弹性模量为n次函数式(13)的函数形式,通过引入γ调整n次项对应的系数,进行功能梯度圆筒模型的研究,得出应变与位移的解析解。此外,对于径向弹性模量的变化,一部分学者还通过建立指数函数来进行研究,Durodola和Attia [18] 假设弹性模量为指数函数式(14)来改变径向弹性模量,研究功能梯度圆筒的特性。Mohammadi和Dryden [20] 则结合幂函数和指数函数,提出一个弹性模量沿径向变化的函数形式式(15),此函数含有多个可调参数,可以灵活的改变函数形状,因而更适合拟合功能梯度材料弹性模量的空间变化。
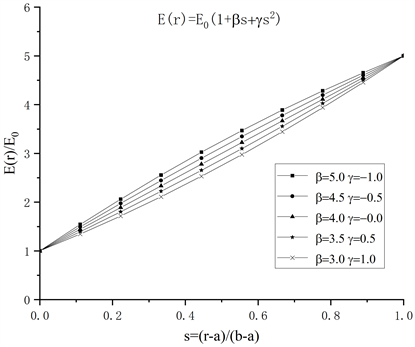
Figure 1. Changes of elastic modulus in literature [17]
图1. 文献 [17] 的弹性模量变化情况

Figure 2. Changes of elastic modulus in literature [18]
图2. 文献 [18] 的弹性模量变化情况
对于多参数假设中关于环向和径向同时改变的弹性模量函数,现有研究相对较少,Chen和Lin [17] 假设三角函数式(16),可以通过系数β和γ既可以实现环向弹性模量的变化,又可实现径向弹性模量的变化。
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
式中,a—圆筒内径;
b—圆筒外径;
r—圆筒测量处的半径;
β、γ、δ、n—无量纲参数。
根据上述三参数假设的弹性模量函数,取式(10)、式(12)绘制图进行对比,当γ = 0或者β = 0时为双参数,γ取其他值时为三参数,可以从图像中看出,使用三参数可以使中间梯度层的杨氏模量较为随意变化。
李昊 [21] 分别采用层合模型和连续梯度模型,使用复变函数方法求解了平面弹性情况下的功能梯度材料圆筒在不同荷载作用后的应力场和位移场,其假设的弹性模量除了采用线性函数、指数函数等特定的单一函数,还引入了任意多阶式式(18)来综合考虑到实际制作中制造方法、材料成分等的多样性。
(18)
式中,ak—常数,k = 0, 1, 2, ∙∙∙;
N—多项式的阶数。
在功能梯度圆筒力学特性分析,现有的对功能梯度圆筒的大多数研究,所假设的荷载往往是轴对称的,对于非轴对称荷载的研究很少。欧阳鬯和徐林林 [22] 对受空间非轴对称荷载的单层有限长空心圆柱体建立了变形分析方法,吴庆良 [23] 采用复变函数法给出了在圆筒外表面受有非均布径向压力作用下单层厚壁圆筒的应力解析解。高永涛等 [24] 采用复变函数方法得出了双层厚壁圆筒外壁受有一类两向不等压非均布径向压力,内壁受有均布压力作用时平面问题的应力求解方法,在两层圆筒光滑接触的假定下获得双层厚壁圆筒的应力解析解。
3. 功能梯度立井井壁
深部岩层原岩应力随着深度的增加而增长,立井井壁的承载能力也需要逐渐增大。为提高井壁的承载能力,现有解决方法主要有提高材料强度、增加井壁厚度、使用功能梯度材料。针对提高材料强度提高立井井壁的承载能力的方法,姚直书等 [25] 学者曾提出混凝土强度提高10 MPa,则井壁承载力将提高约13.8%。可见,此种方法必然会导致成本大额增加,并且混凝土强度较高,井壁会发生脆性破坏。针对增加井壁厚度提高立井井壁的承载能力的方法,张宁等 [26] 学者曾提出对于延伸至1000 m深的竖井,衬砌厚度增加10 mm,钢筋混凝土将增加1%的总成本,而普通混凝土将增加0.25%的总成本。可见,此种方法也会大大增加施工成本,导致材料的大量浪费。因此,较多的国内外学者将功能梯度材料引入了立井井壁,并提出了较多的功能梯度立井井壁的研究以及专利应用。
 (a)
(a) 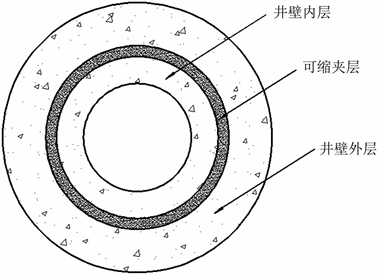 (b)
(b) 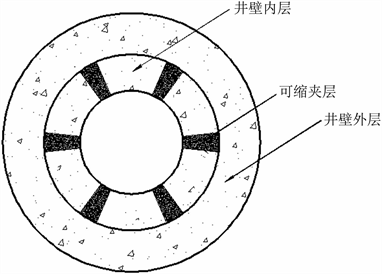 (c)
(c) 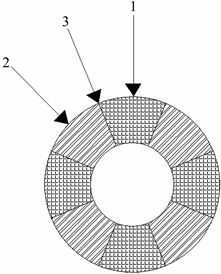 (d)
(d)
Figure 3. Well wall model in patents [27] [28] [30] [31]
图3. 专利 [27] [28] [30] [31] 中的井壁模型
功能梯度材料的材料属性在空间连续变化的特性虽然可以有效的缓解结构中应力集中现象,从而达到“柔性让压”的效果,但这种使材料属性连续变化的特点在实际工程中很难实现,因此不少学者将层合模型的理念引入实际工程中来解决这一问题,即将立井井壁分为多层同轴圆筒结构分层赋予不同材料,从而使材料弹性模量的达到近似连续变化。张宁 [27] [28] 等人基于上述方法提出了一种功能梯度混凝土复合立井井壁及其制作方法,由多层同轴不同弹性模量的结构层组成,由于是采用分层浇筑工艺形成,存在先后次序,使得结构整体性难以保证,如图3(a)所示。李德春等 [29] 在分层浇筑的基础上做出改进,提出整体浇筑的制作方法,有效避免了分层浇筑导致圆筒结构整体性较差的问题。并且,相比于张宁等 [27] [28] 提出的井壁结构仅采用不同弹性模量的圆筒结构层来满足力学承压要求外,李德春等人 [29] 还增加了抗渗、抗水压、抗腐蚀、抗火等同轴混凝土功能层来使井壁可以更好的适应深部地层中复杂的环境。此外,任彦龙 [30] 等人提出两种径向可缩井壁,其本质上也是一种运用功能梯度概念的井壁结构,通过在井壁结构中设置径向可缩夹层,在保证井壁内侧区处于正常使用状态的条件下,允许井壁外侧区产生更大的变形,承受更大比例的外部压力,但如图3(b),图3(c)所示。但是,这种可缩井壁构成较为复杂,实际施工中难以快速施工,且其设计中内外弹性模量的选取没有明确的方法,缺少完善的理论基础。
以上材料参数沿径向改变的功能梯度立井井壁,均是在假设井壁外侧受到的为均布压力的前提下成立的,但实际环境中井壁时常会发生受弯矩作用而产生破坏情况,特别是在复杂的深部地层中井壁往往所受的不是均布的荷载作用。基于此,李德春等 [31] 又提出了一种弹性模量可沿角度方向梯度变化的功能梯度井壁结构,通过将井壁环向分为多块扇形区域配置不同标号混凝土来实现材料参数的梯度变化,从而最大限度地利用混凝土强度,提高了结构的经济适用性,如图3(d)所示。目前关于沿角度方向实现立井井壁的功能梯度特性的应用研究极为缺乏,可考虑在制作方式、结构界面处理等方面进行深入研究。
现有的功能梯度井壁的研究,大多数学者都是先假定出功能梯度井壁中的内外弹性模量,再进行功能梯度圆筒在外荷载作用下的分析研究,这样将不能保证所设置的弹性模量分布为对应荷载形式下最优的分布形式。针对这一不足,吕爱钟和张路青 [32] 采用反分析的方法,通过假设圆筒内的应力状态满足一定预定条件,对功能梯度材料的弹性模量沿立井圆筒径向方向反演推导处最优变化函数,此成果可用于指导立井井壁的设计。许冲 [33] 通过相似模化设计,提出了功能梯度井壁制作技术,获得了功能梯度井壁受力变形规律,基于理论研究成果并运用MATLABAppDesigner开发出了功能梯度井壁结构设计软件,为功能梯度井壁的设计推广提供了技术支持。
4. 功能梯度地铁隧道衬砌
由于隧道衬砌为水平放置结构,使得衬砌上各部分受到的周边地层的压力并不均匀,从而使导出功能梯度衬砌理论模型的精确解较为困难,相关的理论研究较为缺乏。张通通 [12] [34] 等另辟蹊径,提出在实际的结构设计中主要关注的是结构的弯矩和轴力,可运用力法的方法求得,而不必精确得出每一点的应力大小。基于此提出了一种弹性模量沿角度方向以幂函数形式变化的衬砌结构变形模型,并运用力法对模型的函数参数进行分析。结果表明:在衬砌顶部和底部配置高弹性模量混凝土,在中部配置弹性模量相对较低的混凝土有利于减小结构变形;结构的整体刚度提高有利于减小结构变形,具有一定的实际应用参考价值。传统的钢筋混凝土管片功能单一,仅能满足承压需求,但复杂的地下环境对其防水、抗渗、抗蚀、抗裂和抗火能力提出了更高的要求。针对这一不足,马保国 [35] [36] 等人与孔德玉 [37] 等均是利用功能梯度概念,通过将防水、抗渗、抗蚀、抗裂和抗火多种材料功能层叠合,各自分别提出了一种具有高防水、高抗渗、高抗蚀、高抗裂和高抗火性能的多功能盾构管片及其制备方法,而两者的不同主要集中在所使用的材料方面,以及功能层的空间上的排布组合。上述的两者的功能梯度混凝土管片,实现了管片外保护层高防水抗渗、结构层提供强度以及内衬层耐火的多功能一体化特点,主要适用于修建越江跨海隧道和城市地铁。
5. 功能梯度圆筒结构制备方法
功能梯度圆筒结构因其组成材料在空间上的连续性,导致其制作方法的特殊性和复杂性。不过自功能梯度概念引入土木工程领域以来,一些学者也纷纷提出了适应于混凝土材料特性的制作方式。本文主要总结了土木工程领域中研究、应用较为广泛的三种功能梯度混凝土圆筒的制作方式:包括分层浇筑、整体浇筑、3D打印。
5.1. 分层浇筑
分层浇筑制备方式是三种制备方法中最为成熟的,操作最简单的一种。其制备思路是将圆形井壁划分为多层同轴的圆环,从内到外依次分层浇筑,待上一层混凝土达到初凝状态后再开始浇筑下一层,直至最外层浇筑完毕。如张宁 [27] 公开了“一种功能梯度混凝土复合立井井壁及其制作方法”,采用分层浇筑方法指导了功能梯度井壁的现场施工浇筑;孔德玉 [37] 等人公开的“一种高性能梯度功能盾构衬砌管片及其制备方法”以及马保国 [36] 公开的“一种功能梯度盾构管片及其制备方法”两者均是通过分层浇筑的制作方法使得管片含有不同功能层,从而具有高防水、高抗渗、高抗蚀、高抗裂和高抗火等多种性能特点,改变了以往混凝土衬砌管片功能单一的缺点。
优点:操作简单、方便实验室内进行模型制作;
缺点:制作周期较长、工艺繁琐、井壁浇筑质量受过程影响较大,井壁整体性较差。
5.2. 整体浇筑
为了解决分层浇筑导致圆筒结构整体性较差的问题,李德春等 [29] [31] 在分层浇筑的基础上做出改进,从而提出整体浇筑的制作方法。其制作方法与分层浇筑的不同点在于事先在层与层之间放置临时模板用作各层的临时浇筑分界,将各层所需的不同性能的混凝土同时浇筑到对应层中,再通过吊起装置将临时模板移除,并根据实际情况进行振捣。李德春 [29] 等人公开了“一种多层功能梯度立井井壁结构及施工工艺”的专利,通过将井壁结构沿径向均分为多层均等圆环,采用整体浇筑的方式实现了井壁结构的弹性模量沿径向发生改变。此外,李德春 [31] 等人还公开了“弹性模量环向梯度变化的功能梯度井壁结构及施工方法”的专利,通过将井壁结构沿环向均分为8块均等扇形,采用整体浇筑的方式获得了沿环向弹性模量改变的井壁结构。
优点:制作周期较短、结构的整体性较高,可结合机械化设施快速施工;
缺点:对提吊装置要求较高,需要多层混凝土同步施工。
5.3. 3D打印
目前,使用3D打印技术制备功能梯度材料在航天、航空等领域发展较早,但在土木工程领域尚处在发展阶段,相关的制备方法也不是很成熟。不过3D打印制备技术所展现出的高效化、自动化优势具有十分巨大的发展潜力。赖建中 [38] 等人公开的“用于3D打印的功能梯度及密度梯度混凝土材料及其制备方法”专利,展示了一种适用于3D打印的混凝土材料配方,并通过改变轻骨料的掺入量来实现密度梯度层材料的密度呈梯度变化,因此混凝土构件的自重大大降低,其抗震性和结构承载力也得到大幅改善。董赛阳 [39] [40] 等人深入研究了3D打印功能梯度混凝土的制备方法,并对3D打印功能梯度混凝土的抗爆抗侵彻性能展开研究。现有研究大多关注在3D打印混凝土材料本身,而对打印过程中混凝土可连续打印高度随打印路径等参数变化的规律研究较少。针对这一问题,蒋友宝 [41] 等人深入研究了圆环构件在3D打印过程的受力特征、可连续打印高度、打印路径,并基于摩尔–库伦屈服准则和生死单元法建立了3D打印圆环的有限元分析模型。
优点:自动化、精确化、快速化,避免了大量模板的使用;
缺点:制备工艺不成熟,需要适合3D打印系统的特殊混凝土材料。
6. 结论
通过上述功能梯度圆筒力学特性国内外研究现状可以发现,目前的研究仍处在一些的不足,主要体现在以下几个方面:
1) 现有对功能梯度圆筒的研究,所假设的荷载往往是轴对称的,对于非轴对称荷载的研究很少。
2) 现有对功能梯度圆筒的研究,可以考虑通过圆筒切向与径向应力的假设来反演推导出弹性模量在圆筒中的变化,分析弹性模量分布形式。
3) 现有对功能梯度圆筒的研究与专利,关于材料参数的函数假设大都是沿径向变化,对于环向梯度变化的功能梯度圆筒研究较为缺乏。
4) 现有功能梯度圆筒的制备方法较多采用分层浇筑和传统浇筑,3D打印技术的发展为使功能梯度圆筒结构实现连续梯度变化提供了新的思路。
5) 现有的对于功能梯度圆筒的层合模型大多数是多层等分的划分形式,可以考虑在功能梯度圆筒基础上建立N层不等分的层合模型或许会有新的研究思路。
NOTES
*通讯作者。