1. 引言
石英晶体谐振器在电子通讯、军工国防、航空航天等领域都有重要作用,为其能够高频、稳定地工作,科学家对此进行了大量的研究。最初在20世纪50年代,二维板理论Mindlin理论被提出,用于分析压电平板厚度剪切和弯曲振动的问题 [1]。后来,Tiersten在其基础上进行了进一步的扩展,对伸缩振动和面剪切振动加以分析和研究 [2]。1998年,Wang等人又在Mindlin板理论的基础上,扩展得到了高阶Mindlin方程 [3] ,并对其进行了三维有限元分析,得到了AT切石英晶体谐振器的温频关系 [4]。在2011年,台湾大学通过COMSOL软件对石英晶体谐振器的振动模态和电极的影响加以分析和仿真 [5]。2017年,南京航空航天大学对石英晶体圆板谐振器分别进行了二维和三维有限元分析,并将结果分别对照,验证了有限元分析的可行性 [6] [7]。后来,西安电子科技大学的周渭团队对晶体谐振器温度补偿进行了三维有限元分析研究,得到了良好的补偿结果 [8] [9]。随着对晶体谐振器研究的不断深入,有限元仿真逐渐展现了其在谐振器设计与加工方面的优越性。
晶体谐振器尺寸设计的参数直接决定了石英晶体谐振器的各阶振动模态,因此其各项尺寸参数以及加工过程中产生的工艺误差对于石英晶体谐振器的精度和活力有重要的影响。在传统的石英晶体谐振器加工制造工艺中,一般首先通过频率公式确定石英晶片的厚度,再根据经验确定电极的尺寸,最后通过观察晶体谐振器的厚度剪切振动确定晶片的大小。然而这种经验方法很容易导致石英晶体谐振器无法找到最优的厚度剪切振动模态,也很难降低寄生振动造成的模态耦合。因此,通过仿真寻找石英晶体谐振器的振动性能随着尺寸参数变化的规律是十分必要的。
2. 有限元分析建模
2.1. ANSYS材料参数输入
压电材料在收到外界的机械力作用时,会在响应的晶体表面产生电荷,这一现象被称为压电效应 [10]。压电效应是某些单晶的固有特性,如石英、铁电陶瓷、压电聚合物等等。
在ANSYS有限元压电分析中,结构场和电场通过压电参数
耦合:
(1)
(2)
其中,
为应力矢量,
为应变矢量,
为材料的短路弹性刚度矩阵,
为压电应力常数矩阵,
为电位移矢量,
为电场强度矢量,
为夹持条件下的介电常数矩阵。在ANSYS仿真中,我们需要输入的材料参数有弹性刚度矩阵
、压电应力常数矩阵
、介电常数矩阵
、密度
,具体如下:
弹性系数矩阵:
压电应力常数矩阵:
介电常数矩阵:
密度:
需要注意的是,ANSYS软件的参数设定顺序和IEEE标准格式不一致。对于压电应力系数矩阵,应将IEEE格式矩阵中的
作为xy行输入,
作为yz行输入,
作为xz行输入。对于弹性系数矩阵,应将IEEE格式的弹性系数矩阵的
作为xy行输入;
作为yz行输入;
作为xz行输入。
除去石英晶体材料设置外,晶体谐振器电极部分采用银材料,其材料参数如下:
密度:
杨氏模量:
泊松比:
2.2. 建立有限元模型
石英晶体谐振器的结构模型如图1(a)所示。石英晶片上下两面均覆盖有电极,覆盖电极的部分结构如图1(b)所示。
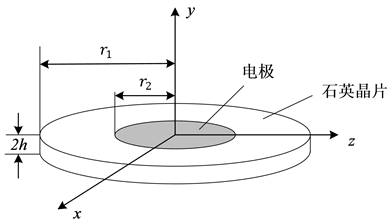 (a) 石英晶振结构图
(a) 石英晶振结构图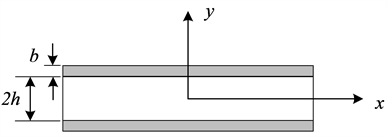 (b) 晶振覆盖电极部分的结构
(b) 晶振覆盖电极部分的结构
Figure 1. Quartz crystal oscillator model structure
图1. 石英晶振模型结构
为石英晶片半径,
为电极半径,h为石英晶片半板厚,b为电极的厚度。本文建模采用4 MHz的圆形石英晶体谐振器,石英晶片半径
为4.325 mm,半板厚h为0.25 mm,电极半径
为2.5 mm,电极厚度为0.1 μm。在仿真中,使用20节点的SOLID226实体单元构建石英晶片,SHELL281单元模拟电极部分,两者采用耦合节点自由度的方法进行连接。在进行有限元网格划分时,采用映射网格划分的方法,圆片厚度方向应划分为至少3个单元。建立模型如图2所示。
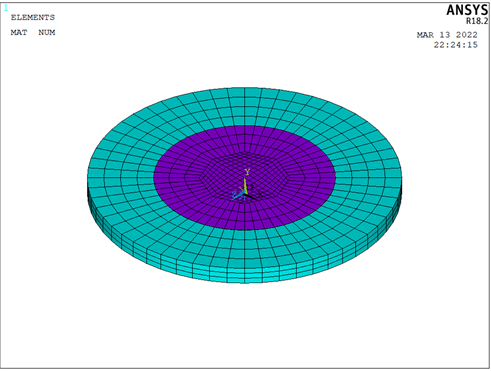
Figure 2. Modeling of quartz crystal resonator
图2. 石英晶体谐振器建模
2.3. 求解
一般来说,可以通过研究石英晶体谐振器的振动情况得出谐振器的性能,在ANSYS中振动情况可以通过其模态分析方法(Model)得出,采用Block Lanczos模态分析方法进行分析,得出如图3所示的厚度剪切振动模态图。

Figure 3. Thickness shear vibration mode diagram
图3. 厚度剪切振动模态图
从图3中可以得出该石英晶体谐振器仿真得到对应的厚度剪切振动频率为
。从振动模态图中可以看出,石英晶体谐振器的振动集中在其上下表面的电极区域,这种现象称之为能陷效应。如图4所示为x轴方向上的归一化振动位移曲线,横坐标表示图中x轴方向上的直径,纵坐标表示该直径上每一节点对应的归一化振动位移的大小。其中UX曲线表示厚度剪切振动位移,UY曲线表示面切变振动位移,UZ曲线表示弯曲振动位移。

Figure 4. Thickness shear vibration displacement curve
图4. 厚度剪切振动位移曲线
从图4中的曲线可以得出,AT切石英晶体谐振器以厚度剪切振动为主,并存在着小幅度的面切变振动和弯曲振动,这些振动被称为寄生振动。寄生振动与主振动之间的耦合程度会很大程度上影响晶体谐振器的性能和活力,因此,如何通过尺寸设计、应力施加等手段尽量减少寄生振动的耦合是晶体谐振器设计和制造过程中的重点问题,尤其是对于圆形的晶体谐振器,由于其材料具有的各向异性,导致对于圆形谐振器的分析与研究相较于矩形谐振器更为复杂。
3. 尺寸参数仿真
3.1. 石英晶片直径
AT切石英晶片的直径除了考虑晶体盒的最大收纳尺寸外,还需要考虑三种寄生振动 [11]:
弯曲振动:
(3)
面切变振动:
(4)
伸缩振动:
(5)
在上式中,
为石英晶片的直径,单位为mm。
为
弯曲振动的泛音次数,应取偶数;
为
面切变振动的泛音次数,取奇数;
为
伸缩振动的泛音次数。晶片半径的选取,原则上应当避免这三种寄生振动对厚度剪切振动的耦合。通过式(3)、(4)和(5)计算,可以得到表1:

Table 1. Wafer diameter of three parasitic vibrations
表1. 三种寄生振动的晶片直径
排除表1中计算得出的数据,可以得出在
应当取8.48 mm到8.68 mm左右。得到不同石英晶片直径对应的厚度剪切振动模态和振动位移曲线结果如图5所示。
图5中当石英晶片直径为8.60 mm和8.65 mm时,石英晶片的寄生振动得到抑制,主振动更加集中于电极区域,而在石英晶片直径为8.70 mm和8.75 mm时,可以很明显的看到其寄生振动模态耦合的增强,根据表1中的数据,可以明显看出在石英晶体直径为8.70 mm时,厚度剪切振动与
伸缩振动发生了耦合,最终导致了谐振器性能下降。
3.2. 石英晶片厚度
石英晶体谐振器的厚度剪切振动频率与石英晶片厚度有很大关系。一般在圆形AT切石英晶体谐振器的设计过程中,厚度剪切振动有如下计算公式 [12]:
(6)
其中,n为谐振器的泛音次数,h为石英晶片半板厚,
为AT切石英晶体的弹性系数,
为晶体密度。将AT切石英晶体的弹性系数带入式(6)中,可以得到:
(7)
式(7)即为AT切晶体谐振器制造工艺中常用的经验公式。其中
,t为石英晶片的厚度。f为频率。由于选用4 MHz的晶体谐振器,根据式(7)可以计算得出晶片厚度应为大约0.415 mm。
如图6所示为石英晶片厚度分别为0.415 mm,0.50 mm和0.55 mm时的振动模态和振动位移曲线。从图中可以得出,在石英晶片厚度为0.50 mm和0.55 mm时,厚度剪切振动主要集中在电极区域,而在石英晶片厚度为0.415 mm时,其厚度剪切振动发生了明显的耦合。因此,在晶振实际设计过程中,应当经过多次测试选择合适的厚度尺寸,尽量避免寄生振动的耦合。
3.3. 电极直径
对于石英晶体谐振器而言,电极直径的确定主要依据石英晶体的等效电阻和静电容的要求。电极的面积直接影响着电阻值和静电容值:电极覆盖的面积大,其静电容大,等效电阻小;与之相反,电极覆盖面积小,其静电容小,等效电阻大 [13]。晶体的等效电阻和静电容与晶体谐振器加工工艺中的每个步骤都有密切的关系,在理论上很难得到准确的估算值,也因此很难得到合适的电极直径和返回频率的理论值,因此,仿真研究电极直径大小对谐振器的影响是十分必要的。
根据能陷理论,振动波的能量应集中于电极区域及其周围,99.9%的能量集中于小于三倍电极尺寸内 [14] ,电极位于晶片中心时,其直径小于三分之一的石英晶片直径,边缘效应就会十分微弱。但是,电极直径过小会导致等效电阻大,影响晶振活力和性能,而电极直径过大则会减弱振动的能陷效应。分别选择电极直径为4.0 mm,4.5 mm,5.0 mm,5.5 mm和6.0 mm进行仿真,结果如图7所示。
由图7可知,当电极直径为5.0 mm和5.5 mm时,可以观察到其寄生模态得到抑制,振动主要集中在电极区域;电极直径为4.0 mm,4.5 mm和6.0 mm时,则相对的寄生振动耦合增加,能陷效应减弱。这说明电极直径大小对于石英晶体谐振器的振动活力有着较大的影响,电极尺寸应当保持在一定尺寸内才能获得理想的振动模态。
表2为不同电极直径下,厚度剪切振动频率变化情况。随着电极直径的增大,厚度剪切振动频率会不断下降,这是由于晶体质量负荷增大造成的。因此,在确定电极尺寸前,应当对晶片振动频率进行预估和模拟,才能得到最优的谐振器性能。

Table 2. Variation of thickness shear vibration frequency of resonator with electrode diameter
表2. 谐振器主振动频率随电极直径变化表
4. 结论
本文研究了AT切圆形石英晶体谐振器石英晶片和电极的尺寸大小对晶体谐振器厚度剪切振动的影响。石英晶片的直径变化对于谐振器寄生振动的耦合程度影响较大,对频率漂移的影响较小,而石英晶片的厚度变化恰恰与之相反。对于电极,电极直径过大或者过小均会造成晶振活力下降,并严重影响谐振器的频率稳定性。