基于服装单品类价格需求分布的研究

Research Based on the Price Distribution of Clothing Single Category

摘要: 服装企业具有销售提前期，需基于市场需求提前做好销售规划。基于市场小生境理论，并聚焦于零售服装领域，分析了服装单品类形成的细分市场以及基于价格维度的需求分布。以零售服装企业的销售数据集为例，选择伽玛分布密度函数、Logistic分布函数、正态分布函数作为参数模型，采用极大似然估计方法，利用Python软件进行需求分布拟合。结果表明，对于服装单品类细分市场，价格与销量的关系可以用伽玛分布密度函数来描述，基于此需求分布可为企业销售规划提供一定指导。

Abstract: Apparel companies have a sales lead time, and they need to make sales plans in advance based on market demand. Based on the market niche theory and focusing on the retail clothing field, this paper analyzes the market segments formed by clothing single categories and the demand distri-bution based on the price dimension. Taking the sales data set of a retail clothing company as an example, we select the gamma distribution density function, the Logistic distribution function, and the normal distribution function to fit the demand distribution of the outerwear category. The re-sults show that, for the clothing single category market segment, the relationship between price and sales volume can be described by the gamma distribution density function. Based on this de-mand distribution, it can provide certain guidance for corporate sales planning.

1. 引言

互联网时代带动了服装电商行业的发展，在全球经济一体化背景下，服装企业竞争方式不断发展变革，随着电商市场上信息逐步透明化，各服装品牌企业在裁剪、面料等基本属性上处于完全竞争状态，品牌间的差异性越来越小，服装商品同质化日趋严重，至此，价格便成为消费者追求高性价比的重要因素，对企业而言价格便成为品牌服装企业经营的一个关键决策点，以往的研究中多集中于服装整体需求分布，而对具体价格区间上的服装需求分布不明，继而会带来销售损失、库存挤压等问题出现。

大数据背景下，数据驱动成为企业经营决策的实践趋势。同时，基于市场小生境理论，Denis Odlin [1] 将其定义为在整个大市场环境下，存在具有稳定需求分布的小市场，因此，专注于服装行业市场，在同一服装品类的细分市场上，将个体对价格的选择进行集中，则海量数据在宏观上呈现出一定稳定趋势的价位分布。且在企业实际业务过程中，大数据背景下呈现的规律性分布进一步证明市场需求呈现一定物理性稳定分布，且在零售领域基于规律分布角度的研究也较为常见，如文献 [2] 研究食品价格与交货提前期的需求概率分布，而以往在服装领域的文献多是基于流行元素 [3] 及流行趋势 [4] 的研究，在价格维度的研究上，赵雅彬 [5] 提出线上与线下商品价格制定的均衡策略，Zhang J [6] 等考虑企业市场实时需求控制商品价格，通过对企业商品价位线的探讨可进一步提高企业自动化经营决策。关于需求分布问题，Matthias Ulrich [7] 考虑库存影响研究需求概率分布，文献 [8] 考虑价格与交货提前期的需求概率分布。此类文献中多是研究关于易逝商品的需求分布，但没有涉及到服装领域基于价位线需求分布问题。

综上所述，本文在大数据背景下引用市场小生境理论，基于价格角度分析服装需求分布。本文利用某大型服装企业的真实销售数据集，先根据历史海量数据分析数据特征选择参数模型，利用极大似然估计法参数模型进行参数估计并进行拟合优度检验确定最终的价格需求分布，本文的研究可为服装企业的精细化运营决策提供一定的思路。

2. 问题描述

2.1. 基于小生境理论的价格需求分布

2.1.1. 小生境理论

小生境理论来源于小生态，小生态原指自然生态系统中在一定环境空间中所栖息的种群部落，彼此间互相制约以此形成较为稳定的小生态系统。市场小生境由小生态演化而来，其概念为整个大市场下一个较为集中的、有针对性的市场，该市场销售特定的产品或服务，并且有稳定的需求和偏好群体。

生态小生境(ecological niche)即是指机体与环境条件之间的关系和在生物群落中所起的作用。因此，整个生物圈可看作是无数个小生态构成的生态系统，彼此之间保持相对动态稳定的状态。小生境理论来源于生态系统间的相互作用，类比于自然生态圈，整个零售市场可以看做是一个具有动态稳定需求的市场，由市场消费者需求与企业商品或服务供应所形成的动态平衡状态。而根据不同领域与场景，整个大市场下可细分为很多个小市场，每个小市场有相对动态稳定需求，这样的市场称之为小生态市场，见图1。

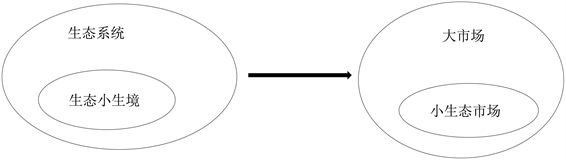
Figure 1. Ecological niche and market niche

图1. 生态小生境与市场小生境

2.1.2. 聚焦于服装领域的小生境理论

聚焦于服装领域，将整个服装市场看作是一个大市场，整个大市场可根据品类可细分至众多小市场，若专注于该市场的外套服装品类小市场，将个体对价位的选择进行集中，那么，根据小生境理论存在有基于价格基础上的稳定需求。同时，也可以通过对比市场总需求分布与该细分市场的需求分布，可以直观展示出两者之间的差距，如整体分布趋势是否与大市场吻合等，发现差异化从而更加有针对性的进行决策优化。见图2。

Figure 2. Clothing category market based on niche theory

图2. 基于小生境理论的服装品类市场

2.2. 数据特征分析

“人”、“货”、“场”作为零售市场三个核心要素，企业在日常经营中围绕三要素形成了销售数据集。

为探究价位与销量的关系，探究价位与销量的关系，笔者筛选出2011年至2014年间外套服装品类价格与销量的销售数据，通过数据可视化得下见图3。可以很直观得出，在基于价位维度上，外套服装品类的销量呈一定稳定分布，首先在整体价格分布上均在0元至500元价格区间，其次四年间销量在同一价格区间的销量分布趋势较为一致，即针对该品类，消费者形成在价位上的稳定需求趋势。同时，为了得出整体的需求趋势线函数模型，根据以往文献中关于需求函数即参数模型的研究 [9] [10] ，以及常见函数曲线分布见图4，选用正态概率密度函数、伽玛概率密度函数以及logistic概率密度函数作为参数模型。

Figure 3. Outerwear category price-sales relationship graph

图3. 外套品类价格–销量关系图

Figure 4. Common distribution model curve

图4. 常见分布模型曲线图

3. 需求分布模型选择

3.1. 常见的概率分布函数

1) 伽玛分布密度函数

伽玛分布概率密度函数为：

$f\left(x,\alpha ,\beta \right)=\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}{x}^{a-1}{\text{e}}^{-\beta x},x\ge 0$ (1)

其中，要求 $x>0$， $\alpha >0$， $\beta >0$， $\Gamma \left(a\right)$ 是上不完全伽玛函数，该函数的定义是：

$\Gamma \left(a\right)={\displaystyle {\int }_0^{\infty }{t}^{a-1}{\text{e}}^{-t}\text{d}t}$ (2)

伽玛分布密度函数包含形状参数 $\alpha$ 与尺度参数 $\beta$，其中 $\alpha$ 决定分布曲线的形状， $\beta$ 决定分布曲线的陡峭程度，根据函数性质当 $\alpha =1$ 时伽玛分布就是指数分布，当 $\alpha =n$ 及 $\beta =1/2$ 时为自由度为n的卡方分布，且伽玛密度函数的分布曲线随参数 $\alpha$ 的与 $\beta$ 取值的不同而形状灵活多变，因此在实际生活中应用广泛。

2) Logistic分布密度函数

Logistic分布密度函数为：

$f\left(x\right)=\frac{{\text{e}}^{\frac{x-\mu }{\sigma }}}{\sigma {\left[1+{\text{e}}^{-\frac{x-\mu }{\sigma }}\right]}^2}$ (3)

Logistic分布函数是一种常见的S型函数，其取值介于0与1之间，分布函数指当n趋于无穷大时，从指数分布中抽取的容量n的随机样本的最大与最小样本值的平均的极限分布。分布函数常用于解决二分类问题的方法，而其密度函数曲线与伽玛及正态分布曲线相似，在相关文献中被作为参数模型进行需求分布拟合，其中， $\mu$ 表示位置参数， $\sigma$ 表示形状参数。

3) 正态分布密度函数

正态分布密度函数为：

$g\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{\text{e}}^{-\frac{-{\left(x-\mu \right)}^2}{2{\sigma }^2}}$ (4)

$x\in R$, $\mu ,\sigma$ 为常数，且 $\sigma >0$，称 $\epsilon$ 服从参数为 $\mu ,\sigma$ 的正态分布，用 $N\left(\mu ,{\sigma }^2\right)$ 表示， $f\left(x\right)$ 表示式可间记为 $N\left(\mu ,{\sigma }^2\right)$ 或 $N\left(\mu ,\sigma \right)$。正态分布曲线广泛存在于自然现象、社会现象以及科学技术及生产活动中，在实际中遇到的许多随机问题都服从或者近似服从正态分布，且近似分布经过一定转换之后，依然服从正态或者近似正态分布，正态分布是最重要的概率分布，在自然科学与社会科学中应用广泛 [11]。

3.2. 参数估计方法

本文采用极大似然估计方法进行参数估计。极大似然估计法是数理统计中参数估计的重要方法之一，该方法利用总体的x的分布函数 $f\left(x;\theta \right)$ (其中x为随机变量， $\theta$ 为参数)的表达式及字样 $x_i\left(i=1,2,\cdots ,n\right)$ 所提供的的信息，建立并求取未知参数 $\theta \left(x_1,x_2,\cdots ,x_n\right)$ 的方法。

极大似然基本原理为：设已知的样本集为： $D=\left\{x_1,x_2,\cdots ,x_n\right\}$，联合概率密度 $P\left(D|\theta \right)$ 称为相对于 $\left\{x_1,x_2,\cdots ,x_n\right\}$ 的 $\theta$ 的似然函数，一般用 $l\left(\theta \right)$ 表示，即：

$l\left(\theta \right)=P\left(D|\theta \right)=p\left\{x_1,x_2,\cdots ,x_n|\theta \right\}={\displaystyle \underset{i=1}{\overset{n}{\prod }}P\left(x_i|\theta \right)}$

如果 $\hat{\theta }$ 是参数结果中能使似然函数 $l\left(\theta \right)$ 最大化的 $\theta$ 值，则 $\hat{\theta }$ 应该是最可能的参数值，那么 $\hat{\theta }$ 就是 $\theta$ 的极大似然估计量，它是样本集的函数，记作： $\hat{\theta }=d\left\{x_1,x_2,\cdots ,x_n\right\}=d\left(D\right)$， $\hat{\theta }\left(x_1,x_2,\cdots ,x_n\right)$ 即被称作极大似然函数的估计值。

$\hat{\theta }=\arg \max l\left(\theta \right)=\arg \max {\displaystyle \underset{i=1}{\overset{n}{\prod }}P\left(x_i|\theta \right)}$

实际应用中，为了便于函数分析，定义了对数似然函数： $H\left(\theta \right)=\ln l\left(\theta \right)$，得：

$\hat{\theta }=\arg \max H\left(\theta \right)=\arg \max \ln l\left(\theta \right)=\arg \max \ln {\displaystyle \underset{i=1}{\overset{n}{\prod }}P\left(x_i|\theta \right)}=\arg \max {\displaystyle \underset{i=1}{\overset{n}{\sum }}\ln pP\left(x_i|\theta \right)}$

4. 需求分布拟合

利用python工具对数据进行拟合，拟合结果见图5。选择筛选出的时间跨度为2011~2014年“外套”服装品类销售数据，维度选择价格与对应销售量进行三个参数模型的参数估计。得到参数估计结果见表1所示，可视化结果见图5所示。

Table 1. Parameter estimation result

表1. 参数估计结果

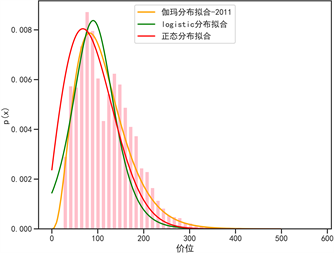
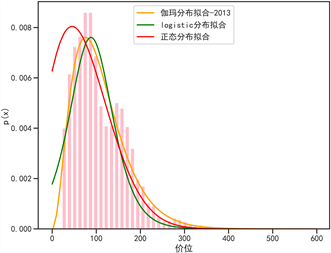
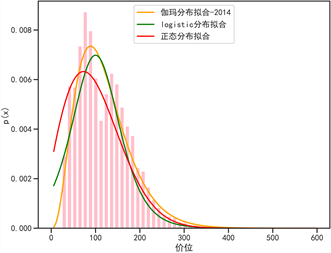
Figure 5. Demand distribution fitting graph

图5. 需求分布拟合图

对拟合效果进行评估，采用如下拟合指标：

$I={\displaystyle \sum {\left(y_i-{y^{\prime }}_i\right)}^2}$ (5)

将原始数据记为 $D=\left[\left\{x_1,y_1\right\},\cdots ,\left\{x_n,y_n\right\}\right]=\left[X,Y\right]$，函数拟合值为 $D^{\prime }=\left[\left\{x_1,{y^{\prime }}_1\right\},\cdots ,\left\{x_n,{y^{\prime }}_n\right\}\right]=\left[X,Y^{\prime }\right]$。其中 ${y^{\prime }}_i$ 表示分布函数的拟合值， $y_i$ 表示实际值，I表示分布函数总的拟合优度。得出本文的拟合值与实际值均为4年数据的平均值，高拟合精度进一步证明选定伽玛分布作为价格需求分布函数的合理性。以上确定了每一年的价格需求分布并验证了合理性，进一步，结合4年时间跨度的数据做了进一步拟合，得到最终的价格需求分布，拟合优度结果如表2所示，可视化结果见图6。

Table 2. Goodness of fit

表2. 拟合优度

Figure 6. Gamma distribution curve

图6. 伽玛分布曲线

如图所示即为最终价位线需求分布曲线。根据公式中伽玛分布概率需求函数参数为： $\alpha =3.7765,$ $\beta =31.1455$。以此得出伽玛分布密度函数可作为该企业外套品类的价格需求分布，此需求分布作为服装规划的决策指导。

5. 结论

本文基于大数据背景下，于市场小生境理论，并聚焦于服装领域市场，说明了服装单品类细分市场下基于价格的稳定需求分布，从理论上证明基于价格需求分布的合理性。在数据的处理上，本文所用数据由某大型服装企业的销售数据集，基于外套品类数据作为研究，即以此为服装市场下的单品类细分市场，以及数据进行数据清洗与可视化分析。其次，通过阅读国内外文献分布模型的研究以及通过对数据特征进行分析，确定以logistic分布密度函数、正态分布密度函数以及伽玛分布密度函数以及作为参数分布模型，并运用点估计方法——极大似然估计进行了各参数模型的参数估计与拟合结果的可视化，并通过拟合优度对比，最终确定伽玛分布作为价格需求分布的函数选择。