从简单线性规划问题看梯度概念的教学引入

Teaching Introduction of Gradient Concept from Simple Linear Programming Problem

摘要: 本文从一个简单的线性规划问题出发，通过介绍高中数学的几何平移法、高等数学的最值求解法和最优化计算方法的图解法来分析梯度概念的引入和应用，让学生在回顾初等数学题目解法的同时，感受高等数学的魅力，体会数学思想方法建立过程中从特殊到一般，从简单到复杂的深刻过程，进一步建立学生分析问题、发现问题、解决问题的能力。

Abstract: Starting from a simple linear programming problem, this paper analyzes the introduction and application of the concept of gradient by introducing the geometric translation method, the maximum solution method and the graphical method of optimization calculation method, so that students can feel the charm of advanced mathematics while reviewing the solution of elementary mathematics problems, and experience the profound process from special to general and from simple to complex in the process of establishing mathematical thought method, and further build the ability for students to analyze, find and solve problems.

1. 引言

高等数学是理工科各专业的重要基础课程，它的很多知识点都会在后续很多课程的学习过程得到体现和验证。但是，这些知识点的实用性在高等数学的课堂教学中往往无法表现出来，这既与课堂教学时间紧张有关，又与教师对概念的深度把握有关。

梯度在高等数学知识体系中是一个相对独立的小概念 [1] [2]，但在后续的数学课程中它却是一个非常重要的概念。由它建立的梯度下降法是最优化计算方法的重要基础，很多工程测算、平差以及深度学习都需要这个基本的方法。梯度的思想萌芽在高中数学的简单线性规划的求解中都已经出现，但是由于受到知识基础限制，教材上只能利用截距和几何平移的办法进行求解。梯度概念在理科本科生后续课程《数值计算方法》 [3] 或工科研究生《最优化计算方法》 [4] 等课程的学习中再次被提及。然而，由于现有教材中鲜有能串起高中和后续数学课程有关梯度概念的应用案例，致使在高等数学的梯度概念教学中学生与梯度相关的先有学习经验准备不足，梯度概念吸收困难，后续课程中待需要应用梯度解决问题时，学生已经忘记了什么是梯度了。基于此，我们以一道线性规划问题为线，通过介绍高中数学的几何平移法、高等数学的最值求解法和最优化计算方法的图解法来分析梯度概念的应用，让学生在对问题的多种解法中加深对梯度概念的理解。

2. 简单线性规划问题的多种求解方法

本求解下列简单的线性规划问题：

$\begin{array}{l}\min -x-3y\\ \text{s}\text{.t}\text{.}x+y\le 6,\\ -x+2y\le 8,\\ x,y\ge 0.\end{array}$

首先利用高中数学的截距法进行平移求解。如图1所示，令 $\lambda =-x-3y$，即 $y=-\frac{1}{3}x-\frac{1}{3}\lambda$，这是一条斜率为 $-\frac{1}{3}$，在y轴上截距为 $-\frac{1}{3}\lambda$ 的直线。当 $\lambda$ 变化时，可以得到一族互相平行的直线。当直线经过可行域上的最高点M时，截距 $-\frac{1}{3}\lambda$ 最大，此时 $\lambda$ 的值最小。解方程组 $\{\begin{array}{l}x+y=6,\\ -x+2y=8,\end{array}$ 得M点的坐标为 $\left(\frac{4}{3},\frac{14}{3}\right)$，代入可得所求最小值为 $-\frac{46}{3}$。

Figure 1. High school mathematics solution diagram for a simple linear programming problem

图1. 简单线性规划问题的高中数学求解示意图

该方法通过几何直观能够很清晰的给出求解过程，学生很容易理解和掌握。但是却无法说明互相平行直线平移的方向有什么意义，更不能处理非线性的优化求解问题。高中的数学教材介绍的很多知识，很大程度上具有高等数学的思想萌芽，将这些萌芽抽象出来再讲解，非常有利于和高等数学进行衔接 [5]。

在利用高等数学最值求解法进行求解。根据二元函数的连续性和极值的相关知识，假设二元函数

$f\left(x,y\right)=-x-3y$, $D_f=\left\{\left(x,y\right)|x+y\le 6,-x+2y\le 8,x,y\ge 0\right\}$,

由于 $D_f$ 为有界闭区域， $f\left(x,y\right)$ 又是初等函数，所以 $f\left(x,y\right)$ 在其定义域 $D_f$ 上肯定存在最小值，并且最小值只能在定义域内部的驻点和定义域边界上的点取得。因为

$\{\begin{array}{l}\frac{\partial f}{\partial x}=-1,\\ \frac{\partial f}{\partial y}=-3,\end{array}$

所以， $f\left(x,y\right)$ 在其定义域内部没有驻点。如图2所示，假设：

$\{\begin{array}{l}{l}_1:x+y=6,\left(0<x<6\right);\\ l_2:y=0,\left(0<x<6\right);\\ l_3:x=0,\left(0<y<4\right);\\ l_4:-x+2y=8,\left(0<x<\frac{4}{3}\right).\end{array}$

在边界 $l_1$ 上，由于 $y=6-x$，利用代入法，此时 $f\left(x,y\right)=2x-18$，视其为一元函数，它的唯一驻点是 $x=9$，由于 $0<x<6$，所以 $f\left(x,y\right)$ 在边界 $l_1$ 的内部没有驻点，同理，函数 $f\left(x,y\right)$ 在其他边界线的内部也没有驻点。综上， $f\left(x,y\right)$ 的可能极值点只剩下边界直线的四个交点，分别代入函数 $f\left(x,y\right)$ 比较大小可知其最小值为 $-\frac{46}{3}$。

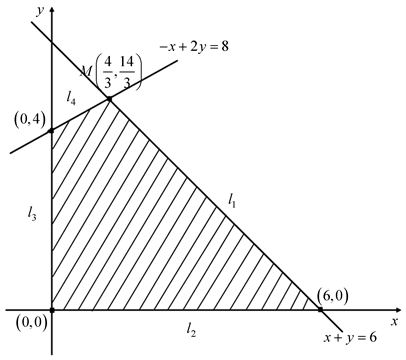
Figure 2. Diagram of solving simple linear programming problems in Advanced Mathematics

图2. 简单线性规划问题的《高等数学》求解示意图

该方法利用极值的定义确定出最值的求解过程，思路清晰，方法也很容易理解，还能够处理非线性优化问题。由于只是处理了一个简单的线性规划问题，显得求解过程却较为繁琐，很多学生在学习过程中甚至想使用高中的办法，没有显示出学习极值的真正意义。

最后利用《最优化理论与算法》中的图解法来求解上述线性规划问题 [6]。如图1所示，先画出这个问题的可行域，它是平面上的一个多边形，顶点分别为

$\left(0,0\right),\left(6,0\right),\left(\frac{4}{3},\frac{14}{3}\right),\left(0,4\right)$

目标函数等值线的方程是 $\lambda =-x-3y$，当 $\lambda$ 取不同数值时得到不同的等值线。等值线的法向量 $n=\left(-1,-3\right)$，也是目标函数的梯度，指向目标函数增大的方向。因此，沿着方向 $n$ 移动等值线时，线上各点目标函数值增大，而沿着 $-n$ 移动等值线时，线上各点目标函数值减小。为求极小值点，沿着 $n$ 方向移动等值线，使它达到极限位置，即达到如若再移动就会出现等值线与可行域的交为空集的位置M，用

上述方法得到极小点 $\left(\frac{4}{3}，\frac{14}{3}\right)$，所求最小值为 $-\frac{46}{3}$，见图3。

该方法利用梯度的知识，简洁地找到了结果，相比高中的方法更加清晰简单，没有那么多的求解过程，还能解决非线性优化问题。但是，此时的学生已经对梯度的概念产生的记忆退化，没有办法感受到梯度的作用，很多时候只能强行认可这样的结论，以至于在后续的有关梯度下降法的学习中都疑惑不解。

3. 梯度概念的教学设计

高等数学关于梯度概念的教学，常规的引入方式是通过寻找最大方向导数开始的，很多高等数学教学工作者也提出了独到的教学设计 [7] [8]，其目的是加深学生对概念的理解。到了后继课程学习时，实际情况是很多学生甚至都忘记了梯度反方向是函数值下降最快的方向。除此以外，很多高等数学教材中都会提到等值线的概念，这需要从二元函数空间区域图像转移到其定义域对应的平面区域图像去解释，很多学生对此也迷惑不解。为解决以上问题，我们在梯度教学的时候，可以尝试通过引入高中数学知识，从学生熟知的线性规划问题出发，利用问题引导式教学方法，深刻感受梯度概念的思想本源以及其数学应用。

Figure 3. Diagram of solving simple linear programming problems in Optimization Theory and Algorithm

图3. 简单线性规划问题的《最优化理论与算法》求解示意图

还利用上述例题：

$\begin{array}{l}\min -x-3y\\ \text{s}\text{.t}\text{.}x+y\le 6,\\ -x+2y\le 8,\\ x,y\ge 0.\end{array}$

讲解过程可以这样设计：这是一个高中都可以解决的线性规划问题，我们首先画出解的可行域，求解过程如上所述的高中方法，这个过程大家都很熟悉。现在，我们换个角度来思考：求解过程中有一族互相平行的直线，它们平移方向有没有什么含义？换个方向行不行？通过观察图1，通过直线平移可以让截距变大，也可以变小，换个方向，同样也可以让截距变化，为什么选择和直线垂直的方向呢？现在再思考一下二元函数 $f\left(x,y\right)$ 的梯度 $\left(-1,-3\right)$，它的反方向恰恰就是平行直线平移的方向，而且这方向截距在变大，并且变大的速率最大，因此目标函数下降的最快，这恰恰是建立梯度概念的思想本源。

继续思考，如果把例题修改为非线性规划问题呢？

$\begin{array}{l}\min -x^2-3y^3\\ \text{s}\text{.t}\text{.}x+y\le 6,\\ -x+2y\le 8,\\ x,y\ge 0.\end{array}$

很显然，我们就不能用截距这个数学概念来求解了，这就需要利用极值或者更高级的处理方法才能求解。高中数学求简单线性规划问题，已经使用到了最简单的梯度思想。我们以学生在高中时代熟知的问题为蓝本，在此基础上介绍函数的梯度，更有助于学生对梯度概念的消化和理解，对梯度概念应用的掌握，以及将来对梯度的应用算法的推广和创新。同时，也让他们看到，初等数学和高等数学并不是割裂开来的，初等数学中的方法实际上是在高一级别的数学工具思想统领下的体现。让他们充分体会到在数学的世界里，站的越高，看的越广。

4. 总结

梯度是优化计算中的一个非常重要的概念，也是计算方法中最常见的方法——牛顿法的理论基础，它有着十分重要的地位，借助高中的知识加强对此概念的理解和分析是一个比较好的教学设计，也能够让学员体会分析问题、发现问题的过程，进一步体会数学学习的奥妙和乐趣。