绝缘体上硅为平台的氮氧化硅波导及马赫–泽德尔干涉仪结构的研究

Study on Silicon Oxynitride Waveguide and Mach-Zehnder Interferometer Structure on Silicon-on-Insulator Platform

摘要: 绝缘体上硅(silicon-on-insulator, SOI)作为光波导的技术平台已在有源和无源光子集成器件中表现出巨大优势。然而，SOI波导过大的折射率差决定了非对称性的很小波导几何尺寸，从而造成较大的光传输损耗、光学耦合与干涉器件过大的偏振相关性和过大的波导–光纤耦合损耗等固有缺陷。本文研究了SOI上以氮氧化硅为芯层氧化硅为包层的波导(简称为氮氧化硅波导)单模条件及由此构成的马赫–泽德尔(MZI)结构，建立了计算光损耗的理论模型。首先，对单模氮氧化硅波导的有效折射率范围和尺寸范围进行了确定，进而对氮氧化硅的直接耦合(DC)型耦合器的传输损耗和耦合区长度Lc的影响进行了系统性模拟，并对MZI结构进行了研究。

Abstract: As a technology platform of optical waveguides, silicon-on-insulator (SOI) has shown great advantages in active and passive photonic integrated devices. However, the large refractive index difference of SOI waveguide determines the small geometrical size of the asymmetric waveguide, which leads to inherent defects such as high optical loss, high polarization dependence, and waveguide-fiber coupling loss. In this paper, both the single-mode condition and the Mach-Zehnder interferometer (MZI) construction of SOI waveguide with silicon oxynitride as core layer and silicon dioxide as cladding layer, which is simply called oxynitride waveguides, are studied, and the theoretical model is established. Then, the effective refractive index range and the other physical parameters of single-mode oxynitride waveguide are determined. Furthermore, the optical propagation loss of waveguides and its influence on the coupling zone length Lc of the directional coupler (DC) are systematically simulated, and the optical loss performance of MZI construction is investigated.

1. 引言

绝缘体上硅(silicon-on-insulator, SOI)目前已经成为被广泛接受的光子集成电路(PLC)技术平台之一，因此对光子学集成器件和系统的开发有着重要作用。作为光信号切换功能的操作单元，马赫–泽德尔干涉仪(MZI)是最常见的机制之一，而光传输损耗(OPL)是光波导器件的核心问题 [1] - [6]。然而，SOI波导过大的折射率差决定了非对称型的小波导结构与几何尺寸，进而造成较大的光损耗、光学耦合与干涉器件过大的偏振相关性和波导光纤耦合损耗等固有缺陷 [7] - [13]。

现代光通信网络锁普遍应用的密集波分复用(DWDM)系统中，开发了各种基于MZI的光波导开关，通过高效控制光相位实现两个输入端和两个输出端之间的光开关功能。因此，基于传统的波导技术Nagai等人于2002年报道了一种基于多模干涉(multimode interference, MMI)型耦合器的MZI的2 × 2光开关，并对MZI结构的光相位响应过程进行了优化 [14]。之后，在本课题组的前期工作中，利用优化的氧化硅波导MZI开关，于2007年发表了小尺寸8 × 8无阻塞矩阵开关 [15]。为了应对新的应用需求，2009年Van Campenhout等人报道了由扩展型MZI结构实现的数字开关功能 [16]。最新的代表性成果是由Soref在2017年报道的，由级联MZI结构实现的波长选择光开关(WSS) [17]。如此可见，氮氧化硅波导和基于MZI的光矩阵开关已经明确显示出巨大的应用潜力 [18]。

本文在SOI平台上研究以氮氧化硅为芯层氧化硅为包层的波导，进而研究其MZI结构，对其传输损耗进行模拟研究以克服SOI波导的光损耗缺陷。同时，由于氮氧化硅波导的芯层折射率可以调整，有利于对波导通道间的耦合与干涉器件的性能优化。另外，相比于传统的氧化硅波导，由于折射率差的大幅度增大使包层和芯层的厚度大幅度减小，从而大大降低了加工难度。为其在光开关及其他光子集成器件中的应用奠定技术基础。

2. 氮氧化硅波导芯层几何尺寸的理论模型

图1是氮氧化硅脊型波导和条型波导的横截面结构，其中波导折射率差变化和波导芯层几何尺寸变化可以用来优化单模条件，同时也对导波模式的分布产生影响。

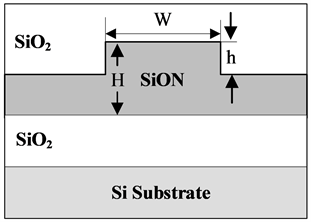
Figure 1. Schematic diagram of standard ridged waveguide cross section

图1. 标准脊型波导横截面示意图

2004年G. T. Reed等人提出了波导几何参数的理论模型，被认为是可以接受的通用性模型。

$\frac{W}{H}\le 0.3+\frac{r}{\sqrt{1-r^2}};r=\frac{h}{H}\ge 0.5$ (1)

方程(1)中，W是脊宽，h和H分别称为外脊高和内脊高，其实内脊高h就是SiON波导的芯层厚度。

在设计波导的几何尺寸满足方程(1)所定义的条件后，使用FD-BPM软件进行模拟，确定由氮氧化硅为芯层氧化硅为包层的脊型波导的有效折射率范围。根据以前的研究结果，在波长为1550 nm，设定芯层氮氧化硅的厚度为：H = 2.0 mm，折射率为1.95时，模拟结果总结在表1中：

Table 1. The better effective refractive index of silicon oxynitride ridge waveguide under partial single mode condition

表1. 部分单模条件下氮氧化硅脊型波导比较好的有效折射率的值

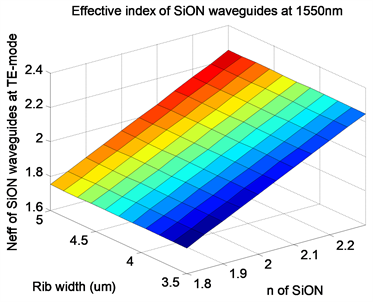
从表1中可以看出，不同的脊高：0.5 μm，1.0 μm和1.5 mm，对于所有脊宽值(W = 1.5~3.5 mm)，TE模式下波导均为单模，而且每一个脊高中有效折射率随脊宽变化很小，但是脊高为0.5 μm时，对应所有的脊宽值，TM模式都不存在。有效折射率值也都非常接近，说明这个氮氧化硅波导结构，有效折射率对脊宽和脊高的变化并不敏感。以上氮氧化硅波导脊波导的特性对于形成干涉与耦合型光波导器件非常有利，因为这样的器件的性能对波导加工容错性非常高。考虑到氮氧化硅波导加工精度方面的影响，所以，选择外脊高为1.2 mm，脊宽从1.5 mm选取到3.5 mm。氮氧化硅的折射率在1.47~2.30内是可调的，所以取1.8~2.3，模拟了单模条件下有效折射率对这两个参数的同步依赖关系，获得了TE和TM模式的有效折射率分布图，分别如图2(a)和图2(b)所示。

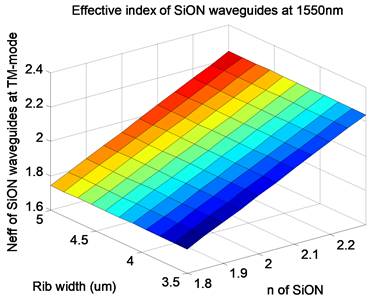(a) (b)

Figure 2. Three-dimensional distribution of effective refractive index of silicon oxynitride ridge waveguide with waveguide width and silicon oxynitride refractive index: (a) TE mode; (b) TM mode

图2. 氮氧化硅脊型波导有效折射率随波导宽度和氮氧化硅折射率的三维分布图：(a) TE模式；(b) TM模式

从此图中，我们对单模分布范围有了整体感，即氮氧化硅波导在单模条件下其有效折射率随着波导脊宽和氮氧化硅芯层的折射率都表现出线性依赖关系，而且是线性依赖关系，这样对选择波导结构实现光波导功能器件的性能指标有了重要的参考。从如图2(a)和图2(b)的比较中可以看出，TE和TM模式之间的有效折射率差距非常小，TM模式下的有效折射率要微小于TE模式下的有效折射率，这种情况是区别于以前的SOI波导的。经过分析发现，TE和TM模式之间的有效折射率差如此小的原因是由于氮氧化硅波导芯层材料和包层材料(氮氧化硅和氧化硅)之间的折射率差很小。所有这些信息不仅为波导结构的选择提供了直接的数据，而且也为后面的MZI结构在偏振相关性方面有所帮助。因此，为进行BPM软件模拟，我们分别选取了BOX层厚度为3.0 μm，上包层厚度为3.0 μm，W = 2.0 μm，h = 1.2 μm和W = 2.5 μm，h = 1.2 μm进行接下来的器件仿真模拟。

3. 氮氧化硅波导基于DC型耦合器的MZI结构理论模型

图3所示的是MZI结构原理图，其中的3 dB耦合器是DC型2 ´ 2耦合器结构，来自光源的光束经过耦合器1，将光束一分为二，一臂为直通臂，另一臂为交叉臂。经过耦合器2进行干涉，使其中一个输出端得到高功率光输出，而另一个输出端得到0或者绝对低的功率输出，并运用此器件计算系统的光损耗和输出端隔离度，以及每个光的输出值的偏振相关性。

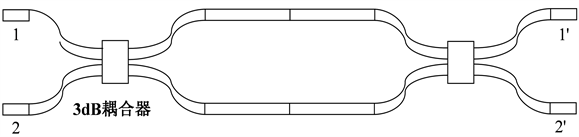
Figure 3. Schematic diagram of MZI structure based on DC type coupler

图3. 基于DC型耦合器的MZI结构示意图

如果两个3 dB耦合器的耦合比和直通比分别为 $\kappa$ 和 $\tau$，两臂光衰减系数和二者之间的光相位差分别为 ${\alpha }_{arm}$ 和 ${\varphi }_{arm}$，对于归一化输入光波电场强度( $E_{in}=1.0$ )，在输入端口1有两个电场强度为 $E_1$ 和 $E_2$ 可以定义为：

$\left[\begin{array}{c}{E}_1\\ E_2\end{array}\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}\tau & {\kappa }^{*}\\ \kappa & -{\tau }^{*}\end{array}\right]\cdot \left[\begin{array}{cc}{\alpha }_{arm}{\text{e}}^{i{\varphi }_{arm}}& 0\\ 0& {\alpha }_{arm}\end{array}\right]\cdot \left[\begin{array}{cc}\tau & {\kappa }^{*}\\ \kappa & -{\tau }^{*}\end{array}\right]\cdot \left[\begin{array}{c}1\\ 0\end{array}\right]$ (2)

于是，两输出端口光强度输出分别为： $I_i=E_i\cdot E_i^{*}$，其中 $i=1,2$ 分别代表输出端1和2，符号*代表复数共轭。利用有限差分算法–光束传播法(FD-BPM)，可得单模有效折射率 $N_{eff}$ 值，进而获得导波模式的传输常数为： ${\beta }_m=\left(2\pi /\lambda \right)N_{eff}$，则其光损耗系数 ${\alpha }_{3D}\left(m\right)$ 则由下式定义(dB/cm) [11]：

${\alpha }_{mzi}\left(m\right)\approx {\alpha }_{arm}\left(m\right)={\alpha }_{3D}\left(m\right)=4.34\left(\frac{{\sigma }_{3D}^2\left(m\right)}{\sqrt{2}{d}^4{\beta }_m}g\left(V\right)\cdot f_e\left(x,\gamma \right)\right)$, (3)

其中 ${\sigma }_{3D}\left(m\right)$ 是波导的三维(3-D)侧壁粗糙度(SWR)，偏振模式分别代表TE和TM模式，所以 ${\beta }_m$ 是导引模式在给定偏振模式下的光传播常数。

4. 利用FD-BPM优化设计DC型2 ´ 2耦合器结构

对于DC型3 dB耦合器，根据之前已确定波导的几何参数即W = 2.0 μm，h = 1.2 μm和W = 2.5 μm，h = 1.2 μm两组数据，我们通过模拟确定了耦合器尺寸：几何参数包括耦合区直波导间距和长度的数值，研究输出端的分束比对与波导几何尺寸误差依赖性最小，以至于不会对由此构成的MZI型波导器件的性能受加工误差的影响。

在模拟过程中通过比较发现，对于3 dB耦合器，其耦合区直波导间长度Lc可以控制的越小，但是由于现阶段的模拟是为以后的芯片器件加工提供理论和数据依据，考虑到芯片器件的光损耗限制。把直波导长度控制在1000 μm以内。最后，在考虑加工精度和芯片器件性能要求的前提下，把耦合区直波导间距设在2.0 μm以下。

通过模拟确定了以下数据与结论，在耦合区直波导间距s = 2.0 μm的情况下，W = 2.0 μm，h = 1.2 μm，Lc = 198.5 μm时，两端输出极为接近且损耗极小，上端输出为0.496886，下端输出为0.496496。总损耗仅不足1%；在s = 1.5 μm的情况下，W = 2.5 μm，h = 1.2 μm，Lc = 242 μm时，两端输出极为接近且损耗极小，上端输出为0.498020，下端输出为0.496527，损耗同样极小。FD-BPM软件模拟过程中还发现对于氮氧化硅为芯层氧化硅为包层的波导，若兼顾到器件加工和性能要求等因素，TE模式优于TM模式。图4(a)和图4(b)分别为TE和TM模式下3.5 μm脊型波导DC型3 dB耦合器的光路模拟图。从图4(a)和图4(b)中可以发现TE模式下的光传输与几何尺寸之间的关系较为明显。则发现了氮氧化硅波导TE和TM模式下的MZI结构光交叉端输出特性的不同。

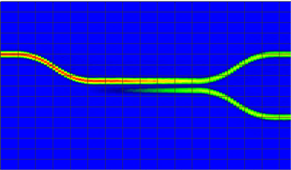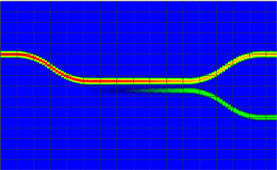(a) (b)

Figure 4. Optical path diagram of 3 dB coupler in TE and TM mode: (a) TE mode; (b) TM mode

图4. TE和TM模式下3 dB耦合器模拟光路图：(a) TE模式；(b) TM模式

在获得较好的3 dB耦合器的各项几何尺寸后，进而与软件模拟相结合模拟基于DC型耦合器(coupler)的MZI结构的光输出性能。对于MZI结构，一共模拟两组数据，分别为W = 2.0 μm，h = 1.2 μm，s = 2.0 μm，Lc = 198.5 μm以及W = 2.5 μm，h = 1.2 μm，s = 1.5 μm，Lc = 242 μm。对于TE模式而言，这两种几何尺寸下较大输出端的输出分别为0.998178和0.999579；对于TM模式而言，两种几何尺寸下较大输出端的输出分别为0.829038和0.846441。

于是，我们可以得出MZI结构相对符合要求的几何尺寸，包括器件总体尺寸设定，上包层和BOX厚度设定和器件细节部分的几何参数。图5为符合设计要求的，模拟光路图。

Figure 5. Silicon oxynitride waveguide based on DC coupler design in line with the expected effect of the optical path diagram

图5. 氮氧化硅波导基于DC耦合器设计的符合预期效果的光路图

从图5中的模拟结果获得：两个结构(2.0 mm和2.5 mm)在交叉输出端TE模式的结果分别为：0.998178和0.999579。TM模式的模拟结果分别是：0.971324和0.969891。目前，能够在SOI基底上加工氮氧化硅波导波导器件，波导在宽度方面的最大加工误差是±0.15 mm。于是，对于2.0 mm宽波导而言，对波导宽度为2.0 − 0.15 mm (即1.85 mm)和2.0 + 0.15 mm (即2.15 mm)两个极限误差值进一步模拟，获得TE模式下在交叉输出端的MZI结构输出值分别为：0.961602和0.978111；获得TM模式下在交叉输出端的MZI结构输出值分别为：0.928514和0.767389。

对于2.5 mm宽波导而言，对波导宽度为2.5 − 0.15 mm (即2.35 mm)和2.5 + 0.15 mm (即2.65 mm)两个极限误差值进一步模拟，获得TE模式下两个极限值状态的MZI结构输出值分别为：0.942914和0.976493；获得TM模式下两个极限值状态的MZI结构输出值分别为：0.919371和0.746101。对以上两个波导宽度及其加工误差极限值处的MZI结构输出值特性分别总结在表2(a)和表2(b)中。

Table 2. Cross output of MZI structure at 2.0 μm and 2.5 μm wide waveguides and their limit errors

表2. 2.0 mm和2.5 mm宽波导及其极限误差处的MZI结构交叉输出

(a): W = 2.0 mm

(b): W = 2.5 mm

从表2(a)和表2(b)中可以发现，对于这两个波导宽度而言，MZI型器件的光输出性能，TM-模式受加工误差的影响要比TE-模式大的多。

5. 结论

由理论研究和以上软件模拟结果可以得出结论，氮氧化硅为芯层氧化硅为包层的波导可以使有效折射率非常均匀，而且TE和TM模式之间的差距也非常小。模拟结果还显示，这种波导的MZI型光学器件在偏振相关性和光学性能对加工误差依赖性方面不仅要比同结构的SOI波导器件优越得多，而且与同结构的氧化硅波导器件相比在偏振相关性和光学性能对加工误差依赖性两个方面都具有优越性，而且加工难度要比SiO₂波导小得多。因此，氮氧化硅波导有利于MZI型光开关等功能器件的研究与应用，尤其在本文对氮氧化硅波导基于DC型耦合器的MZI结构进行研究后，为氮氧化硅波导在光开关及其他光子集成器件中的应用奠定技术基础。

致谢

作者感谢姜伦教授、孔梅教授和陈晨教授在实验中给予的帮助。

基金项目

该工作由吉林省人力资源和社会保障厅人才计划基金(批准号：634190874002)和吉林省科技厅自然科学基金(批准号：201801223JC)共同资助。

NOTES

^*通讯作者。