1. 引言
结构轻量化设计一直是地面武器系统研发过程中的热点方向,同时也是武器装备结构力学性能优化的重要指标之一 [1] [2]。随着现代战争需求的不断提高,对地面武器系统装备的机动性和承载能力提出了更高的要求 [3] [4] [5]。针对于地面机动型武器装备系统,实现其结构系统轻量化设计,能够有效提升武器系统的装载能力、降低系统装备生产开发成本、提升武器整体系统结构可靠性 [6] [7] [8]。
结构拓扑优化方法初期是用于处理类似桁架类结构的优化设计问题,随着有限元技术的不断发展,拓扑优化方法逐渐从离散型结构转变到连续体,为系统结构设计和优化提供了强有力的方法与手段 [9] [10] [11] [12]。目前应用于连续单元体的拓扑优化方法主要有三种,分别是变厚度法、均匀化法和变密度法,其中变密度法是结构拓扑优化较为常用的方法之一 [13] [14] [15]。
某装甲车是由武器装备下方的中托座以及托架共同组成的承载装置,在装备起竖和运输等复杂工况下,需要承受较大的冲击载荷与振动,因此对装甲托架的强度、刚度以及轻量化设计提出了较高的要求。
本文首先针对装甲托架的空间布置要求,建立了包含初始拓扑优化设计区域的装甲托架有限元模型,然后根据六种典型工况对模型进行初步拓扑优化设计,接下来依据拓扑优化结果和结构工艺性要求,通过结构逆向重构方法,重新建立新的装甲托架有限元模型并基于上述工况进行二次拓扑优化,最终得到优化设计结果,经过对比可以发现,相较于初始托架模型,在保证系统刚度和强度不降低的前提下,结构整体质量相较于初始装甲托架结构降低了87.3%。
2. 装甲托架有限元模型及仿真试验
2.1. 有限元模型的建立
在建模软件CREO中创建装甲托架的有限元模型,考虑到与底部车架以及装甲托架左右线路、管路布置等空间要求,建立如图1所示的初始装甲托架模型。
将模型导入有限元仿真软件Hyperworks中,并使用Optistruct模块进行仿真。采用四面体单元对结构进行划分网格,整体结构共有1,175,048个单元,267,507个节点。材料卡片选择ISOTROPIC,Card Image选择MAT1,属性选择3D PSOLID卡片。具体材料参数如表1所示。
2.2. 载荷工况预分析
装甲托架在服役过程中需要承受来自装备以及推力油缸的载荷,具体不同工况下的载荷大小和约束情况如表2所示。

Table 1. Material performance parameters
表1. 材料性能参数表

Table 2. Loads and constraints under different working conditions
表2. 不同工况载荷及约束情况
将上述5组载荷和约束分别添加至有限元模型中,通过有限元分析得到结构的静力学分析结果,具体如图2、图3所示。
从应力和位移云图中可以看出,在前三组工况下,最大位移出现在中托座的端部位置,最大应力点在中托座与托架连接位置处;在4~6工况下,最大位移出现在油缸上支耳点,最大应力点在支耳与中托座连接位置处。具体数值如表3所示。
3. 装甲托架结构拓扑优化
3.1. 拓扑优化理论
变密度法的基本理论是基于假设材料的密度可变,将单元密度当作设计变量,这样就将拓扑优化问题转变成为材料优化问题,根据一定理论算法,使材料达到最优分布,其数学推论为:
(1)
式中,
为每个单元的相对密度;
为每个单元的固有密度;
为拓扑设计变量。

Figure 2. Stress and displacement in working condition 1~3
图2. 工况1~3应力、位移云图

Figure 3. Stress and displacement in working condition 4~6
图3. 工况4~6应力、位移云图

Table 3. Results of maximum stress and displacement under six load conditions
表3. 6种载荷工况最大应力和位移结果
当
时,则为保留的实体材料;当
时,则为去除的实体材料。由于
特性的不连续性,故需拓扑设计变量的连续化,以有效用求导法求解。
(2)
式中,
为单元的刚度;
为单元的固有刚度;
为惩罚因子。
结构的变形能:
(3)
式中,C为结构的柔顺度;F为载荷矢量;K为位移矢量。
将车架的变形能最小作为目标函数,则拓扑优化数学模型为:
(4)
式中,V为充满材料的体积;
为结构设计域的体积;
为密度小于1的材料体积;f为剩余材料百分比;
单元相对密度的下限;
单元相对密度的上限。
3.2. 装甲托架初始结构拓扑优化
基于六组载荷工况的静力学分析结果,对中间设计区域开展拓扑优化。拓扑优化区域为图1中划分的区域,设置优化区域最大应力约束为300 MPa;优化约束为优化部分结构体积分数Volumefrac为初始状态的20%,另外约束前三组工况下,中托座端部位移小于3 mm,后三组工况下油缸上支耳中心位移小于0.2 mm;优化目标为系统柔度最小。
经过11次迭代拓扑优化,将优化结果显示为单元密度,并筛选单元密度大于0.4,得到初始拓扑优化结果密度云图,具体如图4所示。
从图4中可以看出,在已知的六种载荷工况下经过11次迭代最优的材料分布趋势。由于需要考虑到加工工艺和材料成本控制等因素,装甲托架结构需要简化为两组不同直径的管材结构,直径分别为114 mm (壁厚12 mm)和50 mm (壁厚4 mm)。其中上下两组主结构纵向管材需要完全保留,在上下两组管结构中部需要添加合适的管材进行结构加强,以满足结构能承受垂向和侧向的弯曲载荷。因此依照初始拓扑优化结果,在CREO中建立了基于初始优化结构的装甲托架模型,具体如图5所示。

Figure 4. Results of initial topology optimization
图4. 初始拓扑优化结果
在保证产品工艺性和生产成本的条件下,依据图4的初始优化传力路径,在装甲托架上下两组主结构管材中部添加直径为50 mm (壁厚4 mm)的加强管。由于初始拓扑优化结果中,底部的优化传力路径并不明显,因此此处先将底部结构融合,进行进一步的拓扑优化以明确底部结构最优材料分布。
3.3. 装甲托架二次拓扑优化设计
将模型再次导入有限元仿真软件Hyperworks中,并使用Optistruct模块进行仿真,工况设置与初始拓扑优化相同,具体参考表2。二次拓扑优化区域现缩小为图5底部实体设计区域,设置优化区域最大应力约束为300 MPa;优化约束为优化部分结构体积分数Volumefrac为初始状态的20%,另外约束前三组工况下,中托座端部位移小于3 mm,后三组工况下油缸上支耳中心位移小于0.2 mm;优化目标为系统柔度最小。
经过23次迭代优化,将优化结果显示为单元密度,并筛选单元密度大于0.4,得到二次拓扑优化结果密度云图,具体如图6所示。
从图6中可以清晰的看出在六种载荷条件下的材料分布趋势,选取直径为50 mm (壁厚4 mm)的加强管,按照上图中载荷最优传递路线进行布置,最终确定最优的托架结构,具体如图7所示。
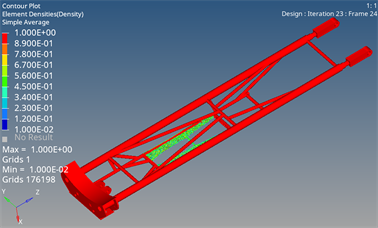
Figure 6. Results of second topology optimization
图6. 二次拓扑优化结果

Figure 7. The optimized bracket model
图7. 优化后装甲托架结构
4. 优化结果对比与验证
经过分步拓扑优化后,确定了最优的装甲托架结构,为确保优化结果的可靠性,需要将最终的优化结果再次施加载荷,查看结构强度和刚度是否满足初始设计要求。通过在有限元软件Optistruct中计算可以得到优化后结构应力和位移云图,其中由于中托座在本次分析过程中无需考虑其应力分布情况,因此将中托座应力隐藏处理,具体如图8、图9所示,左侧为对应工况的位移云图,右侧为对应工况的应力云图。

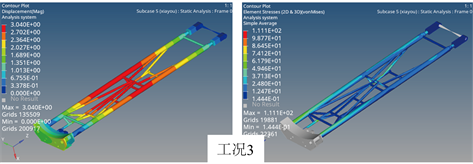
Figure 8. Optimization structure of stress and displacement in working condition 1~3
图8. 工况1~3应力、位移云图——优化后结构

Figure 9. Optimization structure of stress and displacement in working condition 4~6
图9. 工况4~6应力、位移云图——优化后结构
从位移云图中可以看出,停放及运输状态最大位移点出现在托架中部区域,除工况2位移为6 mm,其余两组工况位移均小于4 mm;起竖和发射状态最大位移出现在油缸上支耳中心位置,最大位移均小于0.2 mm。从应力云图可以看出,六组载荷工况下最大应力为218 MPa,当装甲托架选用Q345材料的管型材,仍可保证1.5倍的安全使用系数,可满足结构设计要求。
通过对比优化前后结构形式,具体如图10所示,可以看出在应力水平较低的区域材料通过迭代优化被去除,在需要提高整体弯曲刚度、减小局部应力集中的位置,布置了较多的加强筋。另外列举出优化前后的质量,具体如表4所示,可以看出优化后的装甲托架在保证结构强度和刚度满足设计要求的前提下,相较于初始结构质量降低了87.3%,大大降低了结构质量,降低了生产成本,同时结构仅仅使用了两组不同尺寸的管型材,可以进一步降低生产采购成本,提升产品工艺性。
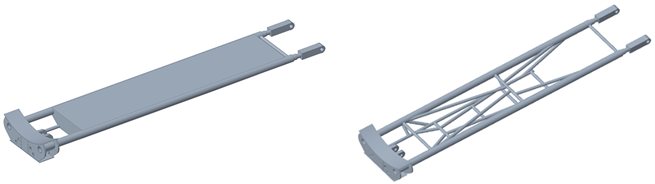
Figure 10. Comparison of structural forms before and after optimization
图10. 优化前后结构形式对比

Table 4. Comparison of structure quality before and after optimization
表4. 优化前后结构质量对比
5. 结论
本文运用分步拓扑优化和有限元联合仿真技术,明确了基于特定载荷工况下装甲托架的结构优化设计,得到最优载荷传递路径下的托架结构,并依照优化结果通过逆向建模得到最终优化结构。本文的主要结论如下:
1) 依据底部车架以及托架左右线路、管路布置等空间要求,建立了结构初始有限元模型,为后续拓扑优化提供了设计基础。
2) 基于典型六种载荷工况,对初始装甲托架模型开展结构强度和刚度分析,确定整体结构的最大应力和最大位移,为后续拓扑优化约束参数提供参考数据。
3) 采用分步拓扑优化的方法,确立了装甲托架的载荷传递形式,并考虑结构工艺性和生产成本,构建了最优装甲托架模型,并通过结构仿真验证,优化后模型在保证结构刚度和强度不降低的前提下,相较于初始装甲托架模型,整体质量降低了87.3%。
NOTES
*第一作者。