Gorenstein MF-投射模

Gorenstein MF-Projective Modules

摘要: 本文引入了Gorenstein MF-投射模的概念，讨论了这类模的基本同调性质，给出了R是半单环时，任意R-模都是Gorenstein MF-投射模的等价刻画，证明了Gorenstein MF-投射维数有限的R-模G都存在特殊的Gorenstein MF-投射预覆盖。

Abstract: In this paper, Gorenstein MF-Projective modules are introduced. We discuss the homological properties of Gorenstein MF-projective modules, give that R is semi-simple ring, and any R-module is a Gorenstein MF-projective module, and prove that any R-module G with finite Gorenstein MF-projective dimension exists special Gorenstein MF-projective precover.

1. 引言

上世纪九十年代，Enochs等引入了Gorenstein投(内)射模和Gorenstein平坦模，这三类模及其维数理论构成了Gorenstein同调代数的理论核心( [1] [2] [3] )。随着Gorenstein同调理论的深入发展，出现了许多重要的研究成果，2010年，Y. Xiang在文献 [4] 中引入了极大平坦模，证明了在左凝聚环上，每一个左R-模存在极大平坦预覆盖。2021年，Yusuf Alagöz在文献 [5] 中引入了MF-投射模，研究了MF-投射模的同调性质以及半单环上MF-投射模的等价刻画。

受以上结论的启发，我们引入Gorenstein MF-投射模，讨论了这类模的同调性质，证明了Gorenstein MF-投射维数有限的R-模G都存在特殊的Gorenstein MF-投射预覆盖。

本文所提到的环均指有单位元的结合环。模均指酉模，除非特别说明，模指左R-模，P(R)表示投射模类、GP(R)表示Gorenstein投射模类， $P{d}_{R}M$ 表示R-模M的投射维数。称M是Gorenstein投射模，如果存在投射模的正合列 $\eta =\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ，使得 $M\cong Ker\left(P^0\to P^1\right)$ ，即对任意投射模 $P\in P\left(R\right)$ ，序列 $Ho{m}_R\left(\eta ,P\right)$ 是正合列。设 $\mathcal{X}$ 是一左R-模类，模M的左(右) $\mathcal{X}$ -分解是指正合列 $\mathcal{X}=\cdots \to X_1\to X_0\to M\to 0$ ( $\mathcal{X}=0\to M\to X^0\to X^1\to \cdots$ )，其中 $X_i\in \mathcal{X},i=0,1,2,\cdots$。称模类 $\mathcal{X}$ 是投射可解类 [6]，如果它包含投射模类，并且在任意短正合列 $0\to A\to B\to C\to 0$ 中，若 $C\in \mathcal{X}$ ，则 $A\in \mathcal{X}$ 当且仅当 $B\in \mathcal{X}$。设 $\mathcal{A}$ 是任意Abel范畴， $\mathcal{B}$ 为 $\mathcal{A}$ 中对像的类。称 $\mathcal{A}$ 中的态射 $\phi :B\to A$ 是对象A的 $\mathcal{B}$ -预覆盖 [7]，如果 $B\in \mathcal{B}$ 且对任意 $B^{\prime }\in \mathcal{B}$ 和任意态射 $f:B^{\prime }\to A$ ，其中 $B^{\prime }\in \mathcal{B}$ ，存在态射 $g:B^{\prime }\to B$ ，使得 $\phi g=f$。

2. Gorenstein MF-投射模

首先，引入Gorenstein MF-投射模，讨论这类模的基本同调性质。

定义1.1 称右R-模M是MF-投射模，如果对任意极大平坦模N， $Ex{t}_R^1\left(M,N\right)=0$。我们将MF-投射模类记为 $MF-P\left(R\right)$。称右R-模M是强MF-投射模，如果对任意极大平坦模N，及任意整数 $i\ge 1$ ， $Ex{t}_R^i\left(M,N\right)=0$。我们将强MF-投射模类记为 $SMF-P\left(R\right)$。

定义1.2 称右R-模M是Gorenstein MF-投射模，如果存在投射右R-模的正合列

$\eta =\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$

使得 $M\cong Ker\left(P^0\to P^1\right)$ ，即对任意MF-投射模N，序列 $Ho{m}_R\left(\eta ,N\right)$ 是正合列。

我们将Gorenstein MF-投射模类记为 $GMF-P\left(R\right)$。

注记 1) $P\left(R\right)\subseteq GMF-P\left(R\right)\subseteq GP\left(R\right)$ ；

2) $GMF-P\left(R\right)$ 关于直和封闭；

3) 由文献 [5] 知，当R是左极大遗传环 [8] 或SF-环时，MF-投射模是Gorenstein MF-投射模；

4) 由对称性，定义1.2正合列 $\eta$ 中所有同态的核、像、余核都是Gorenstein MF-投射模。

命题1.1 设R是环，则以下等价：

1) $M\in GMF-P\left(R\right)$ ；

2) 对任意正整数i，及任意MF-投射模N， $Ex{t}_R^i\left(M,N\right)=0$ ，并且存在 $Hom\left(-,N\right)$ 正合的正合序列 $0\to M\to P^0\to P^1\to \cdots ,P^i\in P\left(R\right)$ ；

3) 存在右R-模的短正合列 $0\to M\to P\to Q\to 0$ ，其中 $P\in P\left(R\right)$ ， $Q\in GMF-P\left(R\right)$。

证明(1) $\iff$ (2)，(1) $\Rightarrow$ (3)显然。

(3) $\Rightarrow$ (1)存在R-模的正合列 $0\to M\to P\to Q\to 0$ ，其中 $P\in P\left(R\right)$ ， $Q\in GMF-P\left(R\right)$ ，对任意MF-投射模N及整数 $i\ge 1$ ，存在 $Hom\left(-,N\right)$ 正合的R-模的正合列

$0\to Q\to P^0\to P^1\to \cdots ,P^i\in P\left(R\right)$ ①

将 $Hom\left(-,N\right)$ 作用在短正合列 $0\to M\to P\to Q\to 0$ 上，对任意正整数i，存在正合序列

$\cdots \to Ex{t}_R^i\left(P,N\right)\to Ex{t}_R^i\left(M,N\right)\to Ex{t}_R^{i+1}\left(Q,N\right)\to Ex{t}_R^{i+1}\left(P,N\right)\to \cdots$

于是由(1)、(2)， $Ex{t}_R^i\left(M,N\right)\cong Ex{t}_R^{i+1}\left(Q,N\right)=0$。

下面考虑R-模M的投射分解

$\cdots \to P_1\to P_0\to M\to 0,P_i\in P\left(R\right)$ ②

令 $K_i=Ker\left(P_i\to P_{i-1}\right)$ ， $i\ge 1$ ， $K_0=Ker\left(P_0\to M\right)$ ，有 $Ex{t}_R^1\left(K_i,N\right)\cong Ex{t}_R^{i+1}\left(M,N\right)=0$ ，由此可得序列②是 $Hom\left(-,N\right)$ 正合的，将正合列 $0\to M\to P\to Q\to 0$ 与序列①和②首尾相接得 $Hom\left(-,N\right)$ 正合的投射模的正合列

$\cdots \to P_1\to P_0\to P\to P^0\to P^1\to \cdots$

且 $M\cong Ker\left(P\to P^0\right)$ ，故 $M\in GMF-P\left(R\right)$。

推论1.1 设M是Gorenstein MF-投射模，则对任意MF-投射维数有限的R-模L，及任意整数 $i\ge 1$ ， $Ex{t}_R^i\left(M,L\right)=0$。

证明由于 $M\in GMF-P\left(R\right)$ ，故存在 $Hom\left(-,\mathcal{M}\mathcal{F}\right)$ 正合的正合列 $0\to M\to P^0\to P^1\to \cdots$ ， $P^i\in P\left(R\right)$ ， $i\ge 1$ ，并且对任意MF-投射模N及任意整数 $i\ge 1$ ， $Ex{t}_R^i\left(M,N\right)=0$。设 $MF-pd\left(L\right)=n$ ，则存在正合列 $0\to L_n\to P_{n-1}\to \cdots \to P_0\to L\to 0$ ，其中 $P_j\in P\left(R\right)$ ， $j=0,\cdots ,n-1$ ， $L_n\in MF-P\left(R\right)$ ，由维数转移可得，对 $\forall i\ge 1$ ， $Ex{t}_R^i\left(M,L\right)\cong Ex{t}_R^{n+i}\left(M,L_n\right)=0$。

引理1.1 设M是Gorenstein MF-投射模，则以下成立：

1) 对任意MF-投射模N及任意整数 $i\ge 1$ ， $Ex{t}_R^1\left(M,N\right)=0$。

2) $P{d}_{R}M=0$ 或 $P{d}_{R}M=\infty$。

证明 1) 因为M是Gorenstein MF-投射模，所以存在一个 $Hom\left(-,MF-P\left(R\right)\right)$ 正合的正合序列 $\cdots \to P_1\to P_0\to M\to 0$ ，其中 $P_i\in P\left(R\right)$ ，则由维数转移可知，对任意MF-投射模N及正整数i， $Ex{t}_R^i\left(M,N\right)=0$。

2) 设 $pd\left(M\right)=m<\infty$ ，则存在正合序列 $0\to P_m\to \cdots \to P_1\to P_0\to M\to 0$ ，其中 $P_i\in P\left(R\right)$ ，令 $K=Ker\left(P_0\to M\right)$ ，则 $MF-pd\left(K\right)\le m-1$ ，故 $Ex{t}_R^1\left(M,K\right)=0$ ，正合列 $0\to K\to P_0\to M\to 0$ 可裂，从而M是投射模。

命题1.2 设 $0\to A\to B\to C\to 0$ 是左R-模的正合列

1) 若A、C是Gorenstein MF-投射模，则B是Gorenstein MF-投射模；

2) 若B、C是Gorenstein MF-投射模，则A是Gorenstein MF-投射模。

证明 1) 由于A、C是Gorenstein MF-投射模，故存在 $Hom\left(-,N\right)$ 正合的正合列

$0\to A\to {P^{\prime }}_0\to {P^{\prime }}_1\to \cdots$

和

$0\to C\to {P^{″}}_0\to {P^{″}}_1\to \cdots$

其中 ${P^{\prime }}_i,{P^{″}}_i\in P\left(R\right)$ ，对任意MF-投射模N及整数 $i\ge 1$ ， $Ex{t}_R^i\left(A,N\right)=0$ ， $Ex{t}_R^i\left(C,N\right)=0$ ，令 $K^{\prime }=\mathrm{Im}\left(A\to {P^{\prime }}_0\right)$ 、 $K^{″}=\mathrm{Im}\left(C\to {P^{″}}_0\right)$ ，由命题1.1知， $K^{\prime },K^{″}$ 是Gorenstein MF-投射模，于是有如下交换图

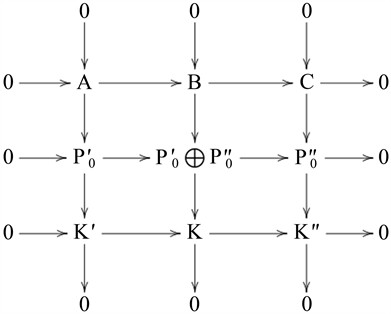
且 $0\to K^{\prime }\to K\to K^{″}\to 0$ 与 $0\to A\to B\to C\to 0$ 有相同的性质，故由马掌引理存在 $Hom\left(-,N\right)$ 正合的正合列 $0\to B\to {P^{\prime }}_0\oplus {P^{″}}_0\to {P^{\prime }}_1\oplus {P^{″}}_1\to \cdots$ ，其中 ${P^{\prime }}_i\oplus {P^{″}}_i\in P\left(R\right),i\ge 1$ ，而且 $Ex{t}_R^i\left(B,N\right)=0$ ，故B是Gorenstein MF-投射模。

2) 由于B是Gorenstein MF-投射模，故存在正合列 $0\to B\to P\to K\to 0$ ，其中 $P\in P\left(R\right)$ ，K是Gorenstein MF-投射模，考虑推出图

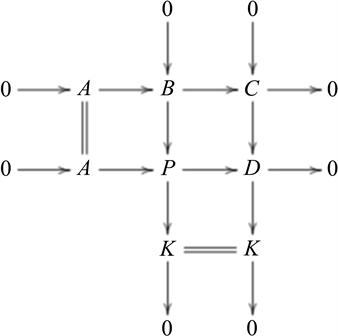
因为C和K都是Gorenstein MF-投射模，所以由(1)知，D是Gorenstein MF-投射模，再利用命题1.1知，A是Gorenstein MF-投射模。

命题1.3 Gorenstein MF-投射模类是投射可解类，且关于直和项封闭。

证明 由 [3] 的定理2.5易证。

推论1.2 在短正合序列 $0\to A\to B\to C\to 0$ 中，若A和B都是Gorenstein MF-投射模，而且对任意MF-投射维数有限的右R-模L及任意整数 $i\ge 1$ ， $Ex{t}_R^i\left(C,L\right)=0$ ，则C是Gorenstein MF-投射模。

证明 由于A是Gorenstein MF-投射模，故存在正合列 $0\to A\to P\to K\to 0$ ，其中 $P\in P\left(R\right)$ ，K是Gorenstein MF-投射模，考虑推出图

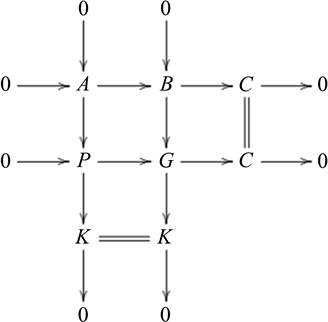
在中间列中，因为B和K都是Gorenstein MF-投射模，故G是Gorenstein MF-投射模，又因为正合列 $0\to P\to G\to C\to 0$ 可裂，故C是Gorenstein MF-投射模。

命题1.4 设R是QF环，则任意Gorenstein MF-投射模都是投射模。

证明 设M是Gorenstein MF-投射模，因为R是QF环，由文献 [5] 知，任意模N都是MF-投射模，故对于任意模N， $Ex{t}_R^1\left(M,N\right)=0$ ，从而M是投射模。

推论1.3 设R是环，则以下等价：

1) R是半单环；

2) R是QF环，并且每一个R-模都是Gorenstein MF-投射模。

证明 (1) $\Rightarrow$ (2)任取R-模M，考虑正合列 $0\to K\to P\to M\to 0$ ，其中 $P\in P\left(R\right)$。因为R是半单环，故 $K\in I\left(R\right)$ ，因此 $0\to K\to P\to M\to 0$ 可裂，则 $K\in P\left(R\right)$ ，从而R是QF环，又因为R是半单环，故M是Gorenstein MF-投射模。

(2) $\Rightarrow$ (1)设M是任意R-模，由(2)知M是Gorenstein MF-投射模，又由命题1.4知， $M\in P\left(R\right)$ ，故R是半单环。

3. Gorenstein MF-投射维数

接下来我们引入模的Gorenstein MF-投射维数，给出Gorenstein MF-投射维数有限的模的等价刻画，结论表明任意Gorenstein MF-投射维数有限的R-模G都存在特殊的Gorenstein MF-投射预覆盖。

定义2.1 设R是环，定义模M的Gorenstein MF-投射维数如下

$\begin{array}{l}GMF-pd\left(M\right)=\inf \{n\in N|存在正合列0\to G_n\to G_{n-1}\to \cdots \to G_0\to M\to 0,\\ 其中G_i\in GMF-P\left(R\right),i=0,1,2,\cdots ,n\}\end{array}$

若上述集合为空集，则规定 $GMF-pd\left(M\right)=\infty$。

我们定义环R的右整体Gorenstein MF-投射维数如下

$r.GMF.PD\left(R\right)=\sup \left\{GMF-pd\left(M\right)|M为右\text{-R}模\right\}$。

关于定义，我们注意到：R是半单环，则 $r.GMF.PD\left(R\right)=0$。

命题2.1 设M是R-模，且 $GMF-pd\left(M\right)<\infty$ ，n是非负整数，则以下等价：

1) $GMF-pd\left(M\right)\le n$ ；

2) 对任意整数 $i>n$ ，及任意MF-投射维数有限的R-模L， $Ex{t}_R^i\left(M,L\right)=0;Ex{t}_R^i\left(M,N\right)=0$ ；

3) 对任意整数 $i>n$ ，及任意MF-投射模N， $Ex{t}_R^i\left(M,N\right)=0$ ；

4) 在任意正合列 $0\to K_n\to G_{n-1}\to \cdots \to G_0\to 0$ 中，若 $G_0,G_1,\cdots ,G_{n-1}$ 都是Gorenstein MF-投射模，则 $K_n$ 也是Gorenstein MF-投射模。

证明 (1) $\Rightarrow$ (2)设 $GMF-pd\left(M\right)\le n$ ，存在正合列 $0\to G_n\to G_{n-1}\to \cdots \to G_0\to M\to 0$ ，其中 $G_0,G_1,\cdots ,G_{n-1},G_n$ 都是Gorenstein MF-投射模，对任意整数 $i>n$ ，及任意MF-投射维数有限的R-模L，由推论1.1及维数转移，得对任意整数 $i>n$ ， $Ex{t}_R^i\left(M,L\right)\cong Ex{t}_R^{i-n}\left(G_n,L\right)=0$。

(2) $\Rightarrow$ (3)显然。

(3) $\Rightarrow$ (4)考虑正合序列

$0\to K_n\to G_{n-1}\to \cdots \to G_0\to M\to 0$ (1)

其中 $G_0,\cdots ,G_{n-1}$ 是Gorenstein MF-投射模，令 $K_i=Ker\left(G_{i-1}\to G_{i-2}\right)$ ， $K_1=Ker\left(G_0\to M\right)$ ， $i=2,\cdots ,n$ ，对任意整数 $i>0$ ，及任意MF-投射模N，由引理1.1及维数转移得， $Ex{t}_R^i\left(K_n,N\right)\cong Ex{t}_R^{i+n}\left(M,N\right)=0$。因为 $GMF-pdM<\infty$ ，且把序列(1)分解成短正合列，类似于文献 [3] 命题2.18的证明，我们可以得到 $GMF-pd{K}_n=GMF-pd{K}_{n-1}-1=GMF-pdM-n$ ，令 $GMF-pd{K}_n=m<\infty$ ，于是存在正合列

$0\to {G^{\prime }}_m\to \cdots \to {G^{\prime }}_0\to K_n\to 0$ (2)

其中 ${G^{\prime }}_0,\cdots ,{G^{\prime }}_m$ 是Gorenstein MF-投射模，令 ${K^{\prime }}_i=Ker\left({G^{\prime }}_{i-1}\to {G^{\prime }}_{i-2}\right)$ ， ${K^{\prime }}_1=Ker\left({G^{\prime }}_0\to K_n\right)$ ， $i=2,\cdots ,m-1$ ，对任意MF-投射模N，用 $Hom\left(-,N\right)$ 作用于正合列 $0\to {G^{\prime }}_m\to {G^{\prime }}_{m-1}\to {K^{\prime }}_{m-1}\to 0$ ，得 $0=Ex{t}_R^1\left({G^{\prime }}_m,N\right)\cong Ex{t}_R^2\left({K^{\prime }}_{m-1},N\right)$ ， $Ex{t}_R^1\left({G^{\prime }}_m,N\right)\cong Ex{t}_R^2\left({K^{\prime }}_{m-1},N\right)\cdots Ex{t}_R^m\left({K^{\prime }}_1,N\right)\cong Ex{t}_R^2\left(K_n,N\right)$ ，

得 $Ex{t}_R^m\left({K^{\prime }}_1,N\right)\cong Ex{t}_R^{m+1}\left(K_n,N\right)$ ，所以 $Ex{t}_R^1\left({K^{\prime }}_{m-1},N\right)\cong Ex{t}_R^m\left(K_n,N\right)\cong Ex{t}_R^{m+n}\left(M,N\right)=0$ ，得 $Ex{t}_R^1\left({K^{\prime }}_{m-1},N\right)=0$ ，由推论1.2知， ${K^{\prime }}_{m-1}$ 是Gorenstein MF-投射模，⋯，依次可得 ${K^{\prime }}_1$ 是Gorenstein MF-投射模，又 $Ex{t}_R^1\left(K_n,N\right)\cong Ex{t}_R^{n+1}\left(M,N\right)=0$ ，故 $K_n$ 是Gorenstein MF-投射模。

(4) $\Rightarrow$ (1)由定义2.1易见。

以下我们给出环R的右整体Gorenstein MF-投射维数有限的等价刻画。

定理2.1 设R是环，整数 $n\ge 0$ ，则以下等价：

1) $r.GMF.PD\left(R\right)\le n$ ；

2) 对任意循环R-模M， $GMF-pd\left(M\right)\le n$ ；

3) 对任意MF-投射模M， $id\left(M\right)\le n$。

证明 (1) $\Rightarrow$ (2)显然。

(2) $\Rightarrow$ (3)任取MF-投射模M，设I是R的右理想，则由(2) $GMF-pd\left(R/I\right)\le n$。由命题2.1知，对任意整数 $n\ge 0$ ， $Ex{t}_R^{n+1}\left(R/I,M\right)=0$ ，则 $id\left(M\right)\le n$。

(3) $\Rightarrow$ (1)设A是任意R-模，B是任意MF-投射模，则由(3) $id\left(B\right)\le n$ ，对任意整数 $i\ge 1$ ， $Ex{t}_R^{i+n}\left(A,B\right)=0$ ，则 $GMF-pd\left(A\right)\le n$ ，故由A的任意性知 $r.GMF.PD\left(R\right)\le n$。

接下来，我们主要研究一个模在什么时候有特殊的Gorenstein MF-投射预覆盖。

定理2.2 任意Gorenstein MF-投射维数有限的R-模G都存在特殊的Gorenstein MF-投射预覆盖。

证明 设 $GMF-pd\left(G\right)=n<\infty$ ，则存在正合列 $0\to C\to P_{n-1}\to P_{n-2}\to \cdots \to P_0\to G\to 0$ ，其中 $P_i\in P\left(R\right),\left(i=0,1,\cdots ,n-1\right)$ ， $C\in GMF-P\left(R\right)$。因为 $C\in GMF-P\left(R\right)$ ，故存在 $Hom\left(-,\mathcal{M}\mathcal{F}\right)$ 正合的正合列 $0\to C\to T_{n-1}\to T_{n-2}\to \cdots \to T_0\to D\to 0$ ，其中 $T_j\in P\left(R\right)$ ， $D\in GMF-P\left(R\right)$ ，可以得到如下交换图：

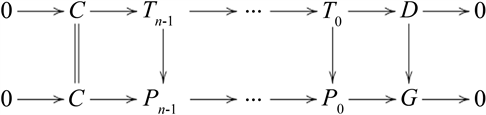
考虑映射锥

$0\to C\to C\oplus T_{n-1}\to P_{n-1}\oplus T_{n-2}\to \cdots \to P_0\oplus D\stackrel{\phi }{\to }G\to 0$

我们可以得到如下正合列

$0\to T_{n-1}\to P_{n-1}\oplus T_{n-2}\to \cdots \to P_0\oplus D\stackrel{\phi }{\to }G\to 0$

令 $K=Ker\phi$ ，则有正合列

$0\to T_{n-1}\to P_{n-1}\oplus T_{n-2}\to \cdots \to P_1\oplus T_0\to K\to 0$

于是 $MF-pd\left(K\right)<\infty$ ，由推论1.2知，对任意Gorenstein MF-投射模 $G^{\prime }$ ， $Ex{t}_R^1\left(G^{\prime },K\right)=0$。 $K\in GM{F}^{\perp }$ ，正合列 $0\to K\to P_0\oplus D\stackrel{\phi }{\to }G\to 0$ 是 $Hom\left(GMF-P\left(R\right),-\right)$ 正合的，即 $P_0\oplus D\stackrel{\phi }{\to }G$ 是G的一个特殊的Gorenstein MF-投射预覆盖。

本文主要研究了Gorenstein MF-投射模的基本同调性质，给出了R是半单环时，任意R-模都是Gorenstein MF-投射模的等价刻画，证明了Gorenstein MF-投射维数有限的R-模G都存在特殊的Gorenstein MF-投射预覆盖。