1. 引言
高超声速飞行器要应对大空域、长时效、高空、高速等严苛的飞行环境,其飞行马赫数Ma一般大于5 [1],穿越稠密大气层时机体对来流空气剧烈压缩,与大气剧烈摩擦产生热量,机体表面将受到巨大的气动加热 [2]。当飞行马赫数Ma大于6时,机体温度高达1900 K,大大超过了现有材料的温度许用极限 [3],为了防止飞行器零部件被高温破坏,就必须对其热防护系统进行研究和设计。
研究发现当CO2达到临界点(临界压力pcr = 7.38 MPa,临界温度Tr = 304.13 K)后气液界面完全消失,形成一个均相状态,因此不仅具有气体的可压缩性而且又具有液体的流动性,使得超临界CO2成为良好的载热工质。由于CO2的热物理性质在跨越拟临界温度(压力值大于临界压力7.38 MPa时所对应的临界温度)时将剧烈变化,进而呈现出特殊的传热特性 [4],如图1所示。相比于常态下的物理性质,在临界点附近,CO2密度急剧降低,比热容和热导率急剧上升,传热能力大大提高。超临界CO2作为循环工质具有以下特性:1) 无毒,不可燃,获取方便,经济性好;2) 粘度接近于气体,密度接近于液体,有良好的传热性能;3) 相比于水,超临界CO2的临界压力和临界温度更容易获得;4) 流动性强,易于扩散,系统循环损耗小,传热效率高;5) 密度大,压缩性好,系统结构紧凑;6) 循环过程中无相变,腐蚀性忽略不计。鉴于以上优点,可以将超临界CO2作为对流传热的冷却介质进行传热保护,即通过在高超声速飞行器壳体内部设计超临界CO2传热管道来突破“热障”。
受飞行姿态的影响,飞行器机体与来流之间的角度并非恒定,所以有必要对不同流动方向的超临界CO2的传热性能进行研究。针对此问题,近十年来,国内外学者对超临界工质在倾斜圆管内的传热特性进行了实验和数值研究。Walisch等人对超临界CO2在不同倾斜管道中的对流换热进行了实验研究。结果表明CO2的比热容和传热效果成正比,且不受雷诺数和倾斜角度的影响;当Re < 104时,受浮力作用影响,传热增强;当104 < Re < 7 × 104时,倾斜角对浮力的影响较大;Re > 7 × 104时,浮力作用对传热的影响

Figure 1. Physical properties of supercritical CO2 at 7.58 MPa
图1. 7.58 MPa下超临界CO2的物理性质
可忽略 [5]。杨传勇等人用数值方法研究了在恒定热流密度加热条件下,管内超临界CO2层流混合的对流和换热情况。研究结果表明,相同工况下,不同倾角下水平流动时传热系数值最大,另外接近于水平流动的30˚和−30˚的倾斜流动传热系数值也较高 [6] [7]。Forooghi等人开展数值模拟,分析了强浮力条件下内径4.4 mm的圆管倾角对沿程的影响,结果表明由于壁面附近速度梯度的改变产生浮力差异进而导致湍流产生的减弱,传热恶化发生,随着倾斜角的减小,传热恶化状况得到改善 [8]。刘新新等人对管径为9 mm螺旋管在不同倾角下的超临界CO2对流换热特性数值研究,研究表明,螺旋管内的周向换热分布受浮力和离心力的影响。随着倾角的减小,螺旋管的非均匀性增强 [9]。Wang等人对内径为20 mm的倾斜圆管进行了数值研究,给出了冷却条件下不同倾角、流动方向和热流通量的湍流流动和传热细节,将倾斜管道中影响超临界CO2流动特性的浮力分解为平行于主流方向和垂直于主流方向的两个分量,认为在类气区域,强制对流占主导地位,几何形状对换热系数的影响不大;在类液区域,浮力增大,自由对流对传热性能有影响,且随着热流密度的增大,影响更为明显 [10]。闫晨帅等人对超临界CO2在内径为10 mm、长度为2000 mm的不同倾斜角度(0˚~90˚)光管内向上流动传热特性进行数值模拟研究。根据拟膜态沸腾理论,闫晨帅等人认为近壁区流体在受热后发生了由类液态至类气态的转化,在壁面处产生可一层类气膜的低密度流体区,管壁热量传递至工质主流核心区域的热阻变大,核心区湍动能减小,产生传热恶化 [11] [12]。
上述关于倾斜角对管流换热的研究,一部分集中在恒定热流密度加热条件下的小直径管(Din < 10 mm)中,另一部分集中在对恒定热流密度冷却条件下大的直径管(Din > 10 mm)中。加热条件下,超临界CO2在大直径斜管中流动换热的研究较少。本文的主要研究目标是对超临界CO2在不同倾角(0˚~180˚)大管中流动的层流混合对流换热性能进行分析,确定不同倾角对其换热系数的影响,分析了重力、流体密度、速度、湍动能、热导率等参数对混合对流传热的影响。本研究结果将为以超临界CO2为传热工质的飞行器换热设备的设计提供指导。
2. 数值方法
2.1. 控制方程
考虑到不同倾斜角下重力的影响,假设流体为三维稳态和湍流流动,忽略与环境的换热。本文采用的稳态雷诺平均Navier-Stokes (RANS)控制方程公式如下:
连续性方程:
(1)
动量方程:
(2)
能量方程:
(3)
上式里的上划横线和波浪线分别表示标量的时间平均和法富尔平均。
Tang等人提出了以下Prt方程 [13],记为TWL模型:
(4)
2.2. 物理模型
图2为本研究所采用的圆管的物理模型。数值工作基于Weinberg的实验展开 [14],计算域包括入口绝热段L1、加热段L2、出口绝热段L3。圆管内径为19 mm,外径23 mm,加热段长度L2为2280 mm。为了消除入口效应,使流体充分发展,加热段前端设置570 mm长的绝热段L1,同时为了避免出口效应,使流体稳定流动,相应地在后端设置150 mm长的绝热段L3。

Figure 2. Physical model of inclined tube
图2. 倾斜圆管物理模型
定义超临界CO2流动方向为z轴正方向,z轴正方向与重力间夹角为θ,规定θ = 0˚代表竖直向下流动,θ = 90˚代表水平向右流动,θ = 180˚代表竖直向上流动。圆管周向角度为φ,定义φ = 90˚和φ = −90˚处分别为圆管顶母线和底母线位置。研究所涉及的9个倾角以及重力加速度在y轴、z轴上的分量如表1所示,其中正值表示轴向正方向,负值表示轴向负方向。

Table 1. Gravity components at different inclination angles
表1. 不同倾斜角下的重力分量
2.3. 边界条件和计算方法
本文主要比较不同倾度θ对超临界CO2流动换热特性的影响,考虑到倾斜流动的不对称性,求解器使用商业软件AnsysFluent 16.0采用双精度,压力基,绝对速度稳态三维计算,不同倾角流动效果通过调整重力在Y轴和Z轴方向上的分量来实现,具体设置见表1。工作压力为7.58 MPa,入口温度287.15 K,经过对比,SST k-ω TWL模型预测效果体现出良好的一致性。物性参数通过NIST REFPROP 9.11编写的RGP格式文件,编写UDF与FLUENT进行耦合来提供。设置入口边界条件为质量流量入口,出口边界条件为压力入口,计算过程中认为管内压力恒定。绝热段和加热段均为无滑移壁面,只在加热段内壁面设置恒定的热流密度,其他均为0。采用有限体积法对控制方程进行离散,压力–速度耦合算法使用SIMPLEC,离散算法先采用一阶迎风,待流场稳定后改为二阶迎风。亚松弛因子设置如表2所示。残差监测值均设置为10−6,除残差以外,监测出口平均温度和加热段壁面平均温度和最高温度,当残差曲线低于10−6且出口温度和加热壁面平均值及最高值监测曲线趋于恒定不变时认为计算收敛。

Table 2. Under-relaxation calculation factor parameters
表2. 亚松弛计算因子参数
2.4. 网格独立性验证
网格质量将直接影响模拟结果,所以有必要先进性网格独立性验证。网格划分在ANSYS ICEM软件内完成,采用六面体结构网格,径向网格采用O型划分,第一层网格高度为0.0002,增长率为1.06,保证所有算例下无量纲壁面距离Y+ < 1,以满足k-ω _SST_TWL湍流模型的计算要求。在前期工作中已经论证过,轴向网格宽度仅对收敛速度有影响,对计算结果几乎没有影响,考虑到计算能力问题,本文网格在Z轴方向上宽度设置为10 mm。圆管径向截面网格划分如图3所示。为了检验网格的独立性,在入口压力P = 7.58 MPa,质量流量G = 564.32 kg/m2·s,恒定热流密度q = 56.7 kW/m2工况下计算了4组不同疏密程度的网格,并将数值结果与实验数据进行了对比。对比结果如图4所示。结果表明,四套网格都准确预测出了壁面温度的发展趋势及传热恶化出现的位置,这也验证了湍流模型选择的合理性。在靠近加热段入口的位置,网格A的预测结果偏差较大,在传热恢复及正常传热阶段,其预测结果又较低于其他网格。随着网格的加密,网格B已经能较为准确的预测整个加热段壁面温度,但是峰值温度较高,且传热恶化出现的位置向偏向上游。对比网格C和网格D的计算结果,二者已经几乎没有差异。考虑到计算准确性以及计算时长问题,本数值工作基于网格总数为4.86 × 106的网格C开展。
Figure 3. Mesh of radial section of circular tube
图3. 圆管径向截面网格

Figure 4. Grid Independence verification
图4. 网格独立性验证
2.5. 模型验证
通过文献调研,对国内外研究超临界CO2传热机理的学者推荐的9种湍流模型进行了计算比较,入口压力P = 7.58 MPa,质量流量G = 564.32 kg/m2·s,恒定热流密度q = 56.7 kW/m2,超临界CO2竖直向上流动,计算结果如图5,从图5可知,k-ω _SST_TWL湍流模型很好地预测了加热壁面上壁温的发展趋势及传热恶化出现的位置,其中峰值温度预测值仅比实验值低13 K,其次峰值温度出现的位置较实验值偏差在5 cm以内,具有较高的预测精度。AKN模型和V2F模型均过高估计了壁面温度的发展,二者均预测出在加热段前端出现传热恶化现象以及接下来的传热增强,但V2F模型预测在加热段后半段将再次发生传热恶化,形成一个驼峰,预测误差较大。其他湍流模型均过低估计了壁温,也未预测出壁温峰值的出现。除此以外,还对Weinberg等人的其他实验进行了验证 [14],均具有较好的预测精度,数值结果和实验值的比较如图6所示,所以文章采用k-ω _SST_TWL湍流模型是合理的,其控制方程及具体参数见2.1节。

Figure 6. Comparison of experimental and numerical results under different heat flux densities when pressure is 7.58 MPa
图6. 当压强为7.58 MPa时不同热流密度下实验与数值结果比较
3. 计算结果与讨论
为了更好地对模拟结果进行处理和分析,定义y-O-z平面与管壁的交线分别为上母线(φ = 90˚)和下母线(φ = −90˚),并对以下各物理量进行定义:
圆管截面流体平均温度为主流温度Tb:
(5)
圆管截面的壁面平均温度Tw:
(6)
圆管壁面换热系数h:
(7)
上下母线温差ΔT:
(8)
壁面局部努赛尔数Nuw:
(9)
上式中,ρ为主流流体密度,u为流体速度,cp为定压比热容,A代表圆管横截面积;in代表内壁面,n代表周向壁面上的节点数;qw代表壁面热流密度。top指上母线,bottom指下母线;h为换热系数,L代表特征长度,在本算例中代表圆管直径,为0.019 m;λb表示主流流体热导率。
3.1. 倾斜角对壁面温度和传热系数的影响
图7给出了不同倾斜角下圆管壁面温度沿程分布和换热系数的分布。从图中可以看出,当流动方向由水平向右变化至垂直向上时(90˚~180˚),壁面温度峰值总体呈上升趋势,水平流动时壁面温度未出现峰值。垂直向上流动时,在加热段前端,靠近壁面的流体温度升高,密度减小,近壁区流体和主流区流体存在较大的温度梯度,热量未能及时传递至主流区域,壁面温度陡升并出现一个尖峰,传热恶化发生。随着主流区流体温度的升高,近壁区流体与主流区流体温度梯度减小,传热逐渐恢复,无论是Weinberg等人的实验数据还是计算结果都显示了在加热段后半段将出现二次壁温峰值 [14],形成一个驼峰。总体来说,随着倾斜角的减小,一次峰值出现的位置逐渐向加热段入口位置移动,且壁面峰值温度持续减小,说明重力对管内超临界CO2的传热有着重要的影响。二次壁温峰值的变化规律与第一次变化规律基本一致,但值得注意的是,当倾斜角为150˚时,二次峰值温度远高于竖直向上流动的二次峰值,在加热段中间位置出现了明显的传热恶化,说明重力不是管内影响超临界CO2传热的惟一因素。传热系数h可用来表征对流换热的强烈程度,换热系数越大,传热效果就越好,对应的壁面温度也就越低。图7中传热系数的变化规律总体和壁面温度的变化规律呈相反趋势。
为了探究倾斜角为60˚时二次峰值陡升的原因,针对不同倾斜角下的圆管在z/d = 85的位置取圆截面。图8为剖面温度云图。除水平流动外,其他角度的截面温度都是不对称的,主流区域上端区域流体温度高于下端,水平流动时差异最为明显,这是因为靠近壁面的流体最先被加热,密度变小,在重力的作用下,出现密度分层,密度最小的流体汇聚于管截面的上部,密度较大的流体沉积在管截面下方。
3.2. 倾斜角对上下母线温度分布的影响
对不同倾角下加热管壁面沿程ΔT的变化和在z/d = 85的位置圆截面半圆周上的努塞尔数的变化进行了分析讨论,分析结果如图9。对于垂直流动,由于流动具有对称性,所以上下母线温差几乎为零。对于倾斜角θ = 120˚,135˚,150˚这几种工况而言,在靠近加热段入口位置,上下壁面温差即出现较大的峰值,且温差峰值随着倾斜角的减小而增大。倾斜角为正时峰值温度远高于水平流动时的上下温差,说明

Figure 7. Temperature distribution and heat transfer coefficient distribution along the wall at different inclination angles
图7. 不同倾斜角下沿程壁面温度分布和传热系数分布
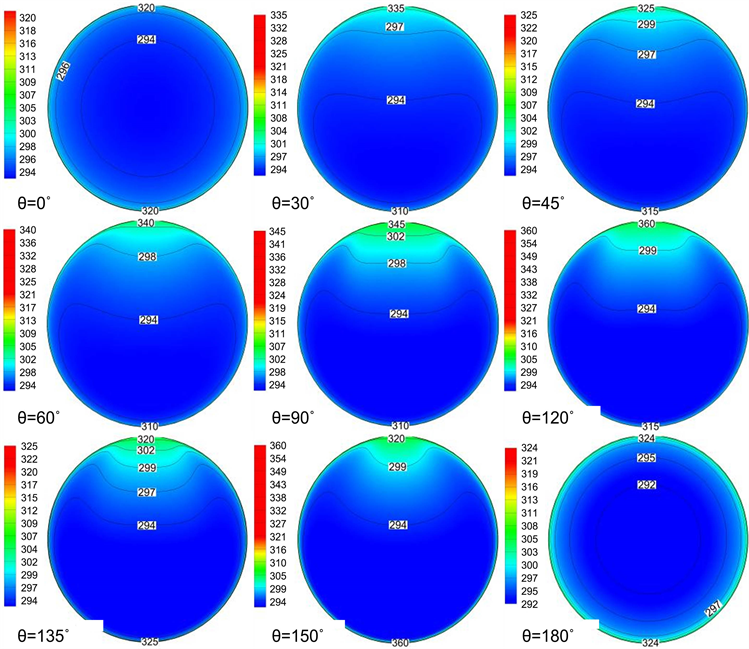
Figure 8. Temperature contour of tube cross section at z/d = 85 at different inclination angles
图8. 不同倾斜角下z/d = 85处截面温度云图
 (a)
(a) 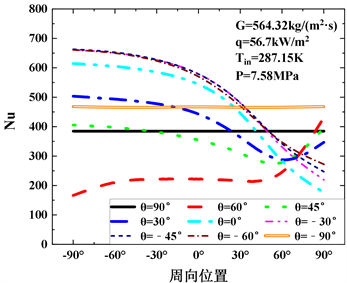 (b)
(b)
Figure 9. Sections at z/d = 85 at different inclination angles. (a) Temperature difference between upper and lower busbars; (b) Radial distribution of Nu from lower busbar to upper busbar
图9. 不同倾斜角下z/d = 85处截面。(a) 上下母线温差;(b) 下母线至上母线径向Nu分布
除了重力,还存在其他的因素影响管流传热。倾斜角为负时上下壁面温差均较小,且温差峰值随着倾斜角的减小而减小,这也验证了向下流动可增强传热。有意思的是,45˚和60˚工况在加热段后半段下母线温度高于上母线温度,θ = 60˚时最为明显,这一现象的研究为搞清楚壁面二次峰值的出现有重要影响。努塞尔数可用来表征流体对流换热强烈程度的一个准数,努塞尔数越大,则表示传热效果越好。对垂直流动,半圆周上努塞尔数为常数,且垂直向下流动的努塞尔数大于垂直向上流动,传热效果更好。图9中横坐标由左到右代表从下母线所在位置沿半圆周到上母线,除垂直流动外,在靠近下母线位置,壁面局部努塞尔数随着倾斜角的减小而增大,水平流动和负角度流动时,沿半圆周方向从下到上努塞尔数减小;正角度下,除θ = 60˚外其他工况从下到上经历了努塞尔数的先减小再增大,θ = 60˚工况下努塞尔数先缓慢增大,在φ = 52˚的位置开始急剧上升。从图中可以看出,正角度流动相比于负角度流动,在靠近下母线位置区域传热效果较差,努塞尔数随着倾斜角的增大而减小;在靠近上母线位置区域传热效果较好,且倾斜角越大,效果越明显。除此以外,对于水平流动和正角度流动,靠近下母线位置区域的传热效果最好,沿圆周越往上母线方向发展,传热效果越差。
3.3. 传热机理分析
为了探究峰值出现的原因,定义Z1 = 1.06处截面为S1,Z2 = 1.615处截取为S2。对S1和S2截面进行分析,横轴代表径向位置,坐标值越小则代表越接近下母线,坐标值越大越接近上母线。分析可知,一次峰值的出现是因为超临界CO2流体进入加热段后,相比于主流核心区,近壁区流体首先被加热,密度减小进而产生较大的密度梯度,对于竖直向上流动,因为密度差管内流体存在浮升力作用且此时浮升力方向与流动方向相同,导致近壁区流体速度增大,竖直向上工况下S1截面出现典型的“M型分布”,其结果如图10。对于水平流动和负角度流动,未出现传热恶化现象,其速度分布没有较大的速度梯度,在整个径向上连续分布。所有的正角度流动都出现了一次峰值,且峰值大小随角度的减小而减小,这是因为垂直流动虽然速度梯度没有其他角度大,但其流动内部结构中未出现二次流,对于近壁区与主流区的对流不产生促进作用,所以速度的变化并未强化换热。θ = 60˚流动在靠近上母线位置速度最大,其次是θ = 45˚流动,最后是θ = 30˚,在靠近下母线位置则完全相反,总的来说θ = 60˚在整个径向上速度差异是最大的,但计算结果显示,在所有出现传热恶化的工况下,θ = 30˚流动的壁面温度峰值最低,这是因为随着重力分量的改变,在S1截面内诱导出现二次流,且二次流强度随重力在y方向上分量的增大而增大,这大大改善了近壁区流体与主流流体的对流换热。竖直向下流动中虽然没有二次流,但是浮力方向与流动方向相反,在一定程度上抑制了速度梯度和分层现象,对换热有一定的促进作用。水平流动和其他负角度流动未出现峰值是因为二次流增强了换热。
为了探究二次峰值出现的原因,从图7可知,在Z2处倾斜角60˚的流动发生明显的传热恶化,其他工况下则为轻微的传热恶化或者强化传热。所以研究S2截面上的物性变化十分必要。图11为圆管S2截面上的物性参数分布,图11(a)可看出,θ = 60˚和θ = 0˚分别在下母线处和上母线处出现了较高的壁面温度,水平流动时,由于重力密度小的流体聚集在截面上端,密度大的流体则沉积在圆管下端,所以上壁面温度较高;而θ = 60˚的流动在下母线处壁面温度值达到360 K,这也是沿程壁面二次峰值出现的直接原因,图11(c)和(d)可以看出,相比于其他工况,倾斜角为60˚时超临界CO2的速度在径向方向经历了剧烈的变化,下母线附近速度最低,上母线附近速度达到最高,分别导致了对换热的抑制和增强,所以倾斜角为60˚时再S2截面处上母线温度最低,下母线温度最高。由于温度升高,使得下母线附近的热导率升高。图11(b)和图12分别表示各工况下S2截面沿径向湍动能变化和湍动能云图,分析图像可知,倾斜角为60˚时在下母线处湍动能非常小,使的这一区域内的流体与主流区流体交换减弱,进而削弱了换热能力。
 (a)
(a) 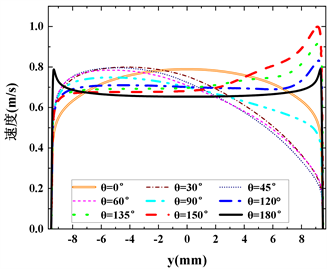 (b)
(b)
Figure 10. At the S1 section of the tube. (a) Radial density distribution; (b) Radial velocity distribution
图10. 圆管S1截面上。(a) 径向密度分布;(b) 径向速度分布
 (a)
(a) 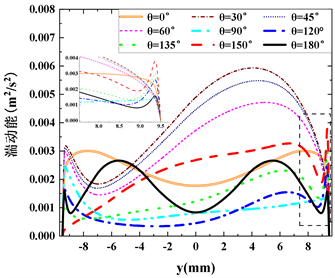 (b)
(b) 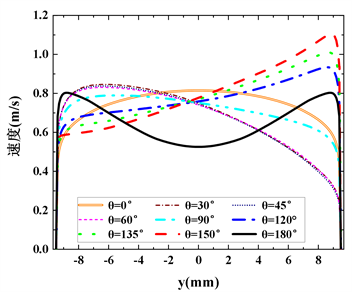 (c)
(c)  (d)
(d)
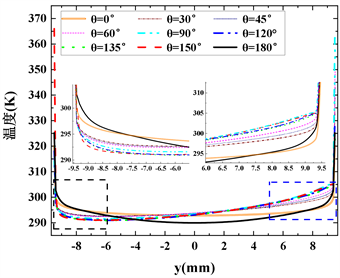
Figure 11. At the S2 section of the tube. (a) Radial temperature distribution; (b) Radial turbulent kinetic energy distribution; (c) Radial velocity distribution; (d) Radial thermal conductivity distribution
图11. 圆管S2截面上。(a) 径向温度变化;(b) 径向湍动能变化;(c) 径向速度变化;(d) 径向热导率变化
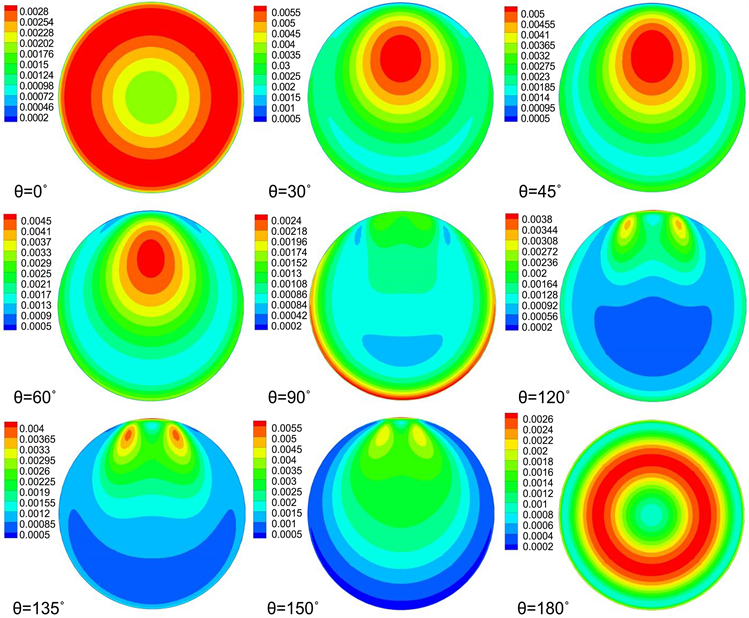
Figure 12. The contour of turbulent kinetic energy at S2 section
图12. 圆管S2截面湍动能云图
4. 结论
本文数值计算了在恒定热流密度加热条件时,D = 19 mm,L = 3000 mm,G = 564.32 kg/m2·s,qw = 10.1~56.7 kW/m2,P = 10.58 MPa条件下,大圆管内超临界CO2流动在不同倾斜角度下的传热表现,通过对不同倾斜角下壁面温度,传热系数,上下母线温度差,壁面局部努塞尔数等影响的研究,得到以下结论:
1) 总体来讲,恒定热流密度加热条件下流动方向与重力方向间夹角大于90˚时将出现传热将受到损害,流动方向与重力方向间夹角小于等于90˚时将出现传热将得到增强,这取决于浮升力的方向与传热介质流动方向是否一致。
2) 数值结果表明当倾斜角为30˚时传热效果最佳,此时壁面温度最低且传热系数最大。
3) 倾斜角的改变在管内诱导出二次流,二次流增强了近壁区流体与主流区流体的热量交换,有利于传热条件的改善。
NOTES
*通讯作者。