新冠肺炎疫情对中国旅游业的冲击影响研究——基于修正的TGARCH-M模型

Study on the Impact of COVID-19 Epidemic on Chinese Tourism Industry

摘要: 新冠肺炎疫情已给我国的旅游业带来了巨大冲击。文章基于2014年1月2日到2021年1月5日共1709个申万旅游综合指数的日度数据，分析了近7年我国旅游业的发展情况。并通过对疫情期间旅游业的综合指数生成过程中融入波动冲击量构建了高拟合程度的服从t分布状态的TGARCH-M模型，研究了新冠肺炎疫情给我国旅游业带来的额外冲击。实证结果表明：我国近7年的旅游业在市场上的波动表现出正反馈效应，正向冲击与负向冲击相比没表现出明显的“杠杆”效应；旅游业在疫情发生前后呈现出不同程度的波动性，疫情发生后旅游业指数的波动冲击额外增加了2.08 × 10−5个单位；但由于额外增加波动冲击值较小，说明疫情对我国旅游业带来的冲击性并不是那么严重，也表明疫情过后旅游业能够以较快的速度恢复。

Abstract: The COVID-19 epidemic has brought a great impact on China’s tourism industry. This paper analyzes the development of China’s tourism industry in the past seven years based on the daily data of 1,709 Shenwan Tourism Composite Index from January 2, 2014 to January 5, 2021. In addition, the TGARCH-M model with high fitting degree following the T-distribution state was constructed by integrating the fluctuating impact amount into the comprehensive index generation process of tourism industry during the epidemic period, and the additional impact of COVID-19 epidemic on China’s tourism industry was studied. The empirical results show that the fluctuation of China’s tourism industry in the market in the recent seven years shows a positive feedback effect, and the positive impact has no obvious “leverage” effect compared with the negative impact. After the outbreak of the epidemic, the Fluctuating impact of tourism index increased by 2.08 × 10−5 units. Due to the small impact value of additional fluctuations, it indicates that the impact of the epidemic on China's tourism industry is not so serious, and it also indicates that the tourism industry can recover at a fast speed after the epidemic.

1. 引言

2020年的春节前后，突然爆发的新冠肺炎疫情给我国的经济社会与人民生活带来了较大冲击。在一年多的疫情期间，中国采取了严格隔离的防控措施，包括封闭城市、边境、限制交通工具出行等，以遏制“新冠肺炎”疫情的传播(王箐等，2020) [1]。事实证明这些措施是有效的，有效地控制住了疫情的恶化。但是这些举措也对我国经济产生了重要影响，如消费减少，产出下降；短期物价上升，失业率上升；金融机构风险增加，产业发展遭受巨大损失等(何诚颖等，2020) [2]。作为一切都建立在以“流动性”特点经营的旅游行业，更遭受了巨大的冲击影响。新冠肺炎疫情可谓为中国的旅游业带来了暂停式的冲击(刘淑芳和杨虎涛，2020) [3]。如今，已有很多学者对我国疫情下的旅游行业进行了深入研究。明庆忠与赵建平(2020) [4] 分析了新冠肺炎疫情影响旅游业的发展机制、特征、表现与后果，并针对本次新冠肺炎疫情防控进程提出相应的管理要求，认为旅游企业、政府与行业协会三方应该共同合作，形成合作共同体以共克时艰。王少华(2020) [5] 对在疫情下的河南省旅游业的冲击表征与影响机理进行了研究，他认为应该正确看待疫情之下旅游业的“危”与“机”。在这严峻的形势下，加强疫情对旅游业冲击波动的系统评估与科学预测，并提出一些有效的恢复旅游业的纾困措施，相信这是学者们当今研究的必然方向(申军波等，2020) [6]。

旅游业是受新冠肺炎疫情冲击与影响的最大行业之一，那么这种影响会持续多久，旅游业是否会恢复到繁荣状态，旅游业未来的发展趋势又是怎么样？众多学者也提出了自己的观点。严伟和严思平(2020) [7] 以中小旅游企业为研究对象，分析了旅游业经济韧性的变迁，认为疫情过后旅游业将保持高恢复效率。王庆生和刘诗涵(2020) [8] 运用数理统计与交叉分析法研究了新冠肺炎疫情后游客的出游意愿与行为，判断疫情过后旅游业的发展趋势并提出了相应的对策。王金伟与王国权等(2020) [9] 对疫情下民众的焦虑心理、出游意愿、以及旅游业的恢复信心三者建模进行了分析，认为这次的疫情可能对公众心理健康和旅游消费的信心产生严重影响。可以看出疫情给旅游业带来了巨大冲击已是不争的事实，但是对未来旅游业的恢复状态与发展趋势，学者们众说纷纭，还是一个未知数。

综上所述，大多数学者都是对新冠肺炎疫情下的旅游业进行定性的分析，即主要研究了疫情对我国旅游业的影响机制，特征，表现与后果，并提出了相关的举措来应对疫情对旅游业的冲击。文章所做的贡献主要在于定量地研究了疫情发生后对旅游行业带来的冲击影响，采用的是时间序列分析方法。在此之前，还没有一篇文献使用时间序列的方法来研究新冠肺炎疫情对我国旅游业造成的冲击影响。经查找，SARS疫情后也只有少数几篇文献运用时间序列分析方法研究我国旅游行业所受到的冲击影响(孙玉环，2006；俞金国等，2005；朱迎波等，2003；桂文林等，2010) [10] [11] [12] [13]。由于文章采用的是金融市场上的旅游行业综合指数数据，在一段时间内可能会存在波动聚集性，所以文章首先会通过偏度、峰度等统计量进行测度，研究指数的波动聚集性；然后再考虑到经济数据上的高风险与高收益之间的关系以及好坏消息对旅游行业所带来的效应大小，构建了TGARCH-M模型。该模型是将指数收益率的条件方差作为前期误差平方项与滞后的条件方差项的线型函数。文章的创新点是在构建了传统的TGARCH-M模型基础上，同时引入表征疫情开始后的虚拟变量，捕捉旅游行业在疫情发生后所遭受到的额外冲击，并分析疫情前后该行业波动性的结构性变化，检验新的信息与旧的信息对波动性的影响。

2. 模型构建与修正

2.1. GARCH族模型介绍

在传统的金融时间序列分析模型中，都是假定随机扰动项的方差为一个定值，可是后来，众多的研究学者发现金融序列的收益率方差在每一个时期并不是一个常数，而是具有明显的异方差性，同时还存在着波动聚集性。在1982年，著名的经济学家Robert Engle (1982) [14] 首先提出金融数据具有异方差性，也是为了建模解决英国的通货膨胀的预报方差而提出的自回归条件异方差模型(ARCH模型)，从此这个模型就被广泛地用来建模并预测金融经济时间序列的波动性。虽然ARCH模型很好地解决了金融时间序列异方差这个问题，但是如果想要ARCH模型的拟合效果更好，就需要增加该模型的滞后阶数，这就会有大量的参数估计，间接增加了模型的复杂度。为了解决这个问题，Bollerslev (1986) [15] 推出广义自回归条件异方差模型，简称GARCH模型，标准的GARCH(p,q)模型的均值方程和条件方差方程结构如下：

$x_t={\phi }_0+{\phi }_1{x}_{t-1}+\cdots +{\phi }_i{x}_{t-i}+{\epsilon }_t$ (1)

${\epsilon }_t={\sigma }_t{v}_t$ (2)

${\sigma }_t^2={\beta }_1{\sigma }_{t-1}^2+{\beta }_2{\sigma }_{t-2}^2+\cdots +{\beta }_p{\sigma }_{t-p}^2+{\alpha }_0+{\alpha }_1{\epsilon }_{t-1}^2+\cdots +{\alpha }_q{\epsilon }_{t-q}^2$ (3)

(3)式中参数具有非负约束，即 ${\alpha }_i\ge 0,i=1,2,\cdots ,q;{\beta }_j\ge 0,j=1,2,\cdots ,p$，且模型中 $v_t$ 独立同分布， $E\left(v_t\right)=0,Var\left(v_t\right)=1$。模型中p与q分别表示GARCH项与ARCH的阶数，系数 ${\alpha }_i$ 代表市场新消息为波动带来的影响， ${\beta }_j$ 代表旧的消息为市场波动带来的影响。

大量研究表明，金融市场上存在着显著的“杠杆效应”，即坏的信息比好的信息所带来的市场波动更大，冲击性更强。1993年，Glosten (1993) [16] 在原有的条件方差方程中增加了一个非对称性选项，该模型被称为门限GARCH模型，也简称为T-GARCH模型。其条件方差方程TGARCH(1,1)模型被设定为：

${\sigma }_t^2={\beta }_1{\sigma }_{t-1}^2+{\alpha }_0+{\alpha }_1{\epsilon }_{t-1}^2+\gamma {\epsilon }_{t-1}^2{d}_{t-1}$ (4)

TGARCH模型是用来解释当信息存在非对称效应时，利用虚拟变量来区分坏的信息与好的信息对收益率波动的影响：当 ${\epsilon }_{t-1}<0$ 时，及坏的信息冲击时， $d_{t-1}=1$ ；否则 $d_{t-1}=0$。 $\gamma {\epsilon }_{t-1}^2{d}_{t-1}$ 称为TARCH项，也称为非对称效应项，当 $\gamma \ne 0$ 时就认为存在着非对称性。易证明当序列受到“坏的信息”冲击时其波动性为 ${\alpha }_1+\gamma$ 倍，受到“好的信息”冲击时其波动减小为 ${\alpha }_1$ 倍。

在金融市场上通常认为资产的收益与风险存在一定的关系，所以经济学家Robert (1987) [17] 提出了GARCH均值模型(GARCH-M模型)，用来研究收益率与风险之间的关系。该模型将代表风险的条件方差加入到均值方程中，其新的均值方程表达式为：

$x_t={\phi }_0+{\phi }_1{x}_{t-1}+\cdots +{\phi }_i{x}_{t-i}+{\epsilon }_t+\delta {\sigma }_t^2$ (5)

此外，在均值方程中还可用条件标准差 ${\sigma }_t$ 或者条件方差的对数形式 $\ln \left({\sigma }_t^2\right)$ 来替代条件方差 ${\sigma }_t^2$。其两种变形分别如等式(6) (7)，本文是构建带有条件标准差 ${\sigma }_t$ 的GARCH-M模型对旅游业综合指数进行波动性分析。

$x_t={\phi }_0+{\phi }_1{x}_{t-1}+\cdots +{\phi }_i{x}_{t-i}+{\epsilon }_t+\delta {\sigma }_t$ (6)

$x_t={\phi }_0+{\phi }_1{x}_{t-1}+\cdots +{\phi }_i{x}_{t-i}+{\epsilon }_t+\delta \ln \left({\sigma }_t^2\right)$ (7)

2.2. 模型修正

由于文章是引用金融市场上的指数数据进行计量研究，即利用旅游业的消费指数做时间序列分析，所以对于金融数据就会表现出具有较高风险而获得较高收益的可能。GARCH-M模型的引入就是来解释旅游行业在存在风险波动的情况下，其收益如何变化，变化多少。文章中收益的变化是依赖于一个常数项，以及旅游行业指数的条件标准差。然后为了证明旅游行业是否存在信息效应的不对称性，就在条件方差的方程中加入非对称效应项(TARCH项)，进而文章构建的识别模型变为TGARCH-M模型。该模型的均值方程为：

$x_t={\phi }_0+{\phi }_1{x}_{t-1}+\cdots +{\phi }_i{x}_{t-i}+{\epsilon }_t+\delta {\sigma }_t$ (8)

对于式子中的残差项 ${\epsilon }_t$，是假定服从t分布。因为研究发现大量的金融数据经GARCH类模型模拟后其残差是不一定近似为正态分布的，会呈现出一定的“厚尾”特征，而t分布恰满足此特征。所以假定残差项服从t分布进行分析更具精准性。

为了研究疫情发生后给旅游行业带来的额外冲击，本文在条件异方差方程中引入表示波动冲击量的虚拟变量 $W_t$。在疫情发生前(文章定义为2020年1月1日之前)时，该值等于0，在疫情发生后(文章定义为2020年1月1日之后)时，该值等于1。其表达式为：

$W_t=\{\begin{array}{l}0,t<2020年1月1日\\ 1,t\ge 2020年1月1日\end{array}$ (9)

因此TGARCH-M模型的条件方差方程变为：

${\sigma }_t^2={\beta }_1{\sigma }_{t-1}^2+{\alpha }_0+{\alpha }_1{\epsilon }_{t-1}^2+\gamma {\epsilon }_{t-1}^2{d}_{t-1}+\rho W_t$ (10)

最后可以根据虚拟变量前的系数 $\rho$ 的显著性来判断疫情发生后是否为旅游业带来了额外的冲击。在统计检验水平显著的基础上，如果 $\rho >0$，说明新冠肺炎疫情给我国旅游业带来了额外的正的冲击，相比疫情之前波动冲击增加了 $\rho$ 个单位；反之，说明疫情下我国旅游业的波动性减小；而在 $\rho =0$ 或统计检验水平不显著下，则认为新冠肺炎疫情对我国旅游业没带来明显的冲击影响。显然，事实表明疫情已经给我国旅游业带来了额外的正的冲击。

3. 数据分析

3.1. 数据选取与处理

新冠肺炎疫情已对中国的旅游业影响将近一年的时间，相对于时间序列模型来说数据还是远远不够的，所以文章中对该指数数据的选取提前至2014年，运用将近7年的数据分析旅游业的收益与波动之间的关系，尤其分析了疫情发生后给旅游业带来的额外冲击影响。所以文章所用的数据是选取2014年1月2日至2021年1月5日共1709个申万旅游综合指数的日度收盘数据，所有数据均来自锐思数据库(http://www.resset.cn/databases)。由于原始数据具有明显的上升趋势，不服从数据的平稳性，所以对原始数据进行了对数处理并计算出对数收益率，下面的分析都是以申万旅游综合指数的日对数收益率为自变量进行估计。

3.2. 描述性统计分析

申万旅游综合指数的日度收盘时序图见图1，从中可以看出旅游业综合指数具有明显的上升趋势，表明我国旅游业的发展规模已十分可观，旅游业市场逐渐繁荣。在2020年之前，旅游业是在稳步发展走向繁荣，但由于新冠肺炎疫情的影响，2020年后旅游业指数出现了大幅度的上升与下降。可明显看出，疫情给旅游业带来了较大的冲击。

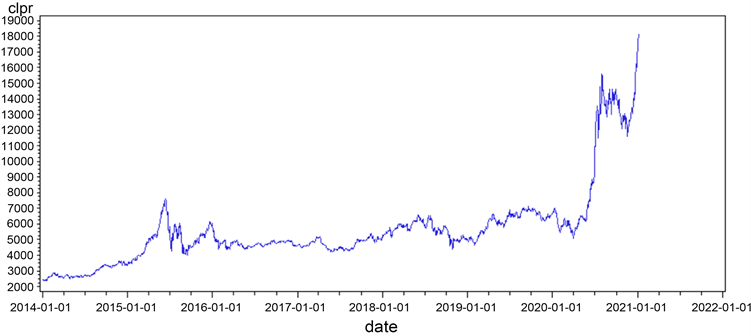
Figure 1. Timing chart of closing price of Shenwan tourism composite index

图1. 申万旅游综合指数收盘价时序图

旅游业综合指数的日对数收益率时序图见图2，根据该图也可看出在疫情发生后旅游业的收益波动

Figure 2. Timing chart of Shenwan tourism comprehensive index yield

图2. 申万旅游综合指数收益率时序图

幅度变大了很多，时序图也存在较为明显的波动聚集现象。根据表1的数据描述性统计分析，收益率的均值为0.00117388，标准差为0.02231067，偏度值为−0.2761364小于0，表明数据为左偏状态，峰度值为3.62582393高于正态分布的峰值3，说明该对数收益率数据为尖峰状态，偏度与峰度的统计量表明该指数的收益率数据具有典型的尖峰左偏的分布特征。对序列的ADF平稳检验，表明收益率序列是平稳的。最后还对收益率序列进行正态分布检验，Shapiro-Wilk统计量也说明该序列不服从正态分布。

Table 1. Descriptive statistical analysis of daily logarithm return rate of Shenwan tourism comprehensive index

表1. 申万旅游综合指数日对数收益率描述性统计分析

注：最后一行为W统计量的正态分布检验，0.940277为统计量值，括号中是p值。

4. 实证结果与分析

4.1. ARCH效应检验

首先对收益率序列进行回归过程，根据对模型系数参数估计的显著性以及AIC与SBC准则，对序列进行滞后第2期和第7期的回归，可得到估计模型：

$x_t=0.0011775-0.06824x_{t-2}+0.08527x_{t-7}+{\epsilon }_t$ (11)

该回归模型的AIC值为−8162.76，SBC值为−8146.43，并且统计量很显著，拟合程度也较好。

接下来采用基于残差平方的Portmanteau的Q检验统计量和拉格朗日乘子LM统计量检验回归后残差的ARCH效应。从表2可看出滞后阶数从1到12阶所对应的统计量p值都显著为0，说明线性回归方程过后的残差序列存在ARCH效应，并且具有高阶的ARCH效应。

Table 2. Residual test of ARCH effect after regression equation

表2. 回归方程后残差序列的ARCH效应检验

4.2. 基于TGARCH-M模型的实证分析

由于检测出收益率序列存在着高阶的异方差性，所以接下来使用广义自回归条件异方差模型来拟合收益率序列。仍然对均值方程进行滞后第2期和第7期的回归，并且采用前面已经修正过后的TGARCH-M模型进行模拟条件方差方程，然后根据AIC与SBC准则确定了TGARCH(1,1)-M模型，所以根据公式(8)和公式(10)拟合出了无截距项的TGARCH(1,1)-M模型：

$x_t=-0.0663x_{t-2}+0.0553x_{t-7}+{\epsilon }_t+0.0874{\sigma }_t$ (12)

${\sigma }_t^2=0.9229{\sigma }_{t-1}^2+2.4144\times {10}^{-6}+0.0794{\epsilon }_{t-1}^2-0.0131{\epsilon }_{t-1}^2{d}_{t-1}+2.08\times {10}^{-5}{W}_t$ (13)

对申万旅游综合指数日对数收益率序列模拟修正后的TGARCH(1,1)-M模型后的参数估计见表3。由结果可看出非对称项的系数估计不显著，说明申万旅游综合指数对于好坏消息所造成的冲击波动无明显差别，也说明了旅游行业在面向正向冲击与负向冲击时没表现出非对称性。表3中除了非对称项的系数不显著外，剩余的参数都至少在概率水平为5%下显著，并且条件方差方程系数之和小于1，满足平稳条件。条件方差方程中的TGARCH项和TARCH项的系数分别为0.9229与0.0794，分别代表该指数的旧信息和新信息对旅游行业的波动性影响，可明显看出旧信息对旅游业市场波动的影响要远远大于新的信息所产生的影响。可知本次新冠肺炎疫情对旅游业就是新的信息所造成的影响，所以这种影响是有限的，对旅游业的冲击并不会太大，该行业的波动冲击持续性还是主要受以前旧的信息影响。

Table 3. TGARCH(1,1)-M model parameter estimation

表3. TGARCH(1,1)-M模型参数估计

从表3可看出文章假设的虚拟变量——波动冲击量( $W_t$)前面的系数 $\rho =2.08\times {10}^{-5}>0$，说明我国新冠肺炎疫情发生后对我国的旅游业波动性平均增加了2.08 × 10⁻⁵个单位，表明疫情的发生对中国旅游业带来了额外的冲击。但是，波动冲击系数 $\rho$ 值仍然较小，说明疫情对中国旅游业带来的冲击性并不是那么严重，也表明疫情过后旅游业的恢复也并不是那么困难。对于文章研究的波动冲击量也对未来中国旅游业的恢复与振兴提供了理论支撑。

表3中的TDFI值对应的是t分布，第二部分模型构建与修正中已经说明文章构建的TGARCH(1,1)-M模型的残差项 ${\epsilon }_t$ 假定服从t分布，因为t分布能够更好地拟合金融数据的尖峰厚尾特征，能够提高模型的精准度。从结果也可明显看出TDFI值对应的p值显著为0，即说明文章中假定残差项 ${\epsilon }_t$ 服从t分布是合理的。

文章在旅游业综合指数收益率均值方程中包含了条件标准差项 ${\sigma }_t$ 的原因是为了在收益率序列生成过程中融入风险度量，构建均值方程。从模型拟合后的结果发现 $\delta =0.0874>0$，满足“收益与风险成正比”的经典假设。也说明了对于我国旅游业的预期风险每增加1%时，就会导致其收益平均增加0.0874%。

最后根据修正后的TGARCH(1,1)-M模型拟合出了申万旅游综合指数日对数收益率的波动情况，如图3所示。图中浅色的线为对数收益率的时序图，深色的线为波动率序列的时序图。从图中可明显看出，该模型所计算出的条件异方差值能够很好地拟合出收益率序列的波动程度；根据波动特征可以发现，波动具有较强的聚集性，即一个较大的波动后面往往跟着一系列大的波动，而一个平缓的波动后面也跟着一系列平缓的波动；同时可以看出波动率上升的速度与下降的速度几乎保持一致，没表现出明显的杠杆效应。因此，申万旅游综合指数日对数收益率与时变波动率的序列图所解释的结果与模型参数估计结果一致，该模型是适应的。

注：浅色线代表对数收益率时序图，深色线代表波动率序列时序图；横坐标的每一小格代表一个季度。

Figure 3. Sequence diagram of log return and time-varying volatility of Shenwan tourism comprehensive index

图3. 申万旅游综合指数对数收益率与时变波动率序列图

从图3可看出旅游业在2015至2016年间波动性较大，意味着受到了一次较大的冲击；并且在2020年的春节后遭受了新冠肺炎疫情的影响后，时变波动率序列图也表现出较大幅度的上升或下降。根据图3并联系实际情况对我国旅游业在2020年的新冠肺炎疫情下做比较分析：2020年的第一个季度是中国新冠肺炎疫情大爆发时期，此时国家各个地区都采取“限流”，“限访”，“限行”等防控措施，甚至还出现了“封城”等强制行动，把以“流动性”为鲜明特征的旅游行业降到了冰点。从图3中可明显看出在2020年的第一个季度，旅游业综合指数绝大多数都是负的收益率，说明该行业遭受了严重的冲击。后来在国家政府有效的管控下，中国疫情在2020年第二个季度时得到了缓解，此时被困在家中几个月后的中国公民也具有了出去旅游的强烈愿望，反映在图3的对数收益率时序图上，就是2020年的第二三个季度。此时，我国旅游业突然“火热”起来，出现了反弹式的增长，前一季度的疫情似乎对旅游业的发展具有了一定的“刺激”作用，第二三季度同第一季度相比获得了更多的正收益。在2020年的最后一个季度，我国某些地区疫情出现了反弹，再加上此时是全球其他国家疫情的高爆发时间，我国公民也具备了较强的防疫意识，我国的旅游业又渐渐变得冷淡。综上所述，可证明我国旅游业的综合指数收益率与波动率时序图分析得出的结果与我国旅游业在新冠肺炎疫情下的实际表现相符合，也间接表明了本次模型的构建很成功。

5. 总结

文章选取2014年1月2日至2021年1月5日的1709个申万旅游综合指数的日度收盘数据，构建TGARCH-M模型，研究了在疫情的影响下，旅游业所遭受的冲击影响。研究结果发现：申万旅游综合指数的日度收盘数据序列具有典型的高峰、肥尾、有偏的统计特征，序列在不同的时期表现出不同的波动性，呈现出明显的“波动聚集性”；我国的旅游业是一个风险与收益成正比的行业，该行业的预期风险每增加1%时，就会导致其收益平均增加0.0874%；我国的旅游业面对市场信息的正向冲击与负向冲击时没表现出明显的“杠杆”效应。

另外，在条件异方差方程中引入表示波动冲击量的虚拟变量，构建修正后的TGARCH-M模型。从结果看出新冠肺炎疫情的发生对我国的旅游业的冲击量平均增加了2.08 × 10⁻⁵个单位，表明疫情发生对我国旅游业还是带来了额外的影响。但是，波动冲击量值较小，说明疫情对我国旅游业带来的冲击性并不是那么严重，也表明疫情过后旅游业的恢复也并不是那么困难。模型结果中的条件异方差方程中的TGARCH系数远大于TARCH系数，也表明旧信息对旅游业市场波动的影响要远远大于新的信息所产生的影响。从长远来看，2020年的新冠肺炎疫情就属于新的信息对旅游行业的影响，所以其影响程度并不是很大。

由申万旅游综合指数时序图发现：近七年，我国旅游业的发展呈上升趋势，总体规模十分可观。2015年至2016年间的该行业受到了较大冲击，以及2020年的新冠肺炎疫情也给该行业带来了影响，但是最后也阻挡不了我国旅游业的蓬勃发展趋势。在疫情期间，旅游行业虽多次降到了冰点，但是当疫情稍微缓解后，该行业就会突然“火爆”起来，因为疫情过后的人们都想出去走走。疫情可谓对旅游行业的发展具有一定的“刺激”作用，即使在疫情期间，旅游行业的总体指数也是上涨的趋势，相信当疫情真正过去后，该行业会以更快的速度发展。

文章的不足在于：第一，鉴于数据与指标的可得性与科学合理性，文章只选取了申万旅游综合指数的日度收盘数据进行建模分析，但这并不能完全代表中国旅游市场整个行业，所以模型结果的精准度与可信度还有待提高。第二，新冠肺炎疫情至今已在中国蔓延一年时间，但对于时间序列分析方法而言，一年的数据序列还是较少，这对最后结果的分析也会造成一定的误差。并且，迄今为止疫情还在全球范围内延续，不知何时新冠肺炎疫情才会完全消失，所以在接下来一段时间，对于文章中所研究的对象中国旅游业还会遭受持续冲击，旅游行业所遭受的额外冲击可能会更大。

参考文献