基于改进DMPs的下肢助行机器人步行楼梯的轨迹规划

Trajectory Planning of Lower Limb Walking-Assistant Robot Walking Stairs Based on Improved DMPs

摘要: 为了辅助下肢功能障碍患者实现在不同尺寸楼梯行走，运用改进的动态运动基元(DMPs)结合机器人运动学分析规划下肢助行机器人运动轨迹和步态。首先，基于D-H模型，建立下肢助行机器人末端机构位姿与各关节角度的关系。然后，使用改进DMPs模仿预先采集到的正常人体步行楼梯轨迹曲线，根据楼梯高度和宽度参数修改目标点，泛化后得到适应新场景的轨迹曲线。再运用机器人逆运动学分析，规划出适应于不同尺寸楼梯的下肢助行机器人踝关节和髋关节运动轨迹。经过仿真实验验证，基于改进的DMPs结合逆运动学分析能有效地规划助行机器人运动的步态，使机器人能适应不同参数的楼梯行走。

Abstract: In order to assist patients with lower limb dysfunction to walk on stairs of different sizes, improved dynamic movement primitives (DMPs) combined with robot kinematics analysis were used to plan the trajectory and gait of the lower limb walking-assistant robot. At first, the relationship between the posture of the end mechanism and the angles of each joint was established based on D-H model. Then, the improved DMPs were used to simulate the trajectory curve of normal human walking stairs, and the target points were modified according to the height and width of the stairs. After generalization, the trajectory curve adapted to the new scene was obtained. Then, the trajectory of ankle joint and hip joint of the robot adapted to stairs of different sizes is planned by using inverse kinematics analysis of robot. The simulation results show that the improved DMPs combined with inverse kinematics analysis can effectively plan the gait of the walking aid robot so that the robot can adapt to stair walking with different parameters.

1. 引言

全球每年新增脊髓损伤患者有25万到50万，脊髓损伤发生率约为10.4~83人每百万人 [1]。脊髓损伤患者中有相当一部分最终会截瘫失去下肢运动能力。下肢助行机器人能有效地为下肢机能损伤患者提供支撑，并帮助患者完成平地行走、步行楼梯等下肢运动。合理规划下肢助行机器人行走步态，能更有效安全地帮助下肢功能不全患者重获下肢运动能力。

目前，日本筑波大学推出了HAL外骨骼，可帮助双腿瘫痪、胸部以下截瘫患者站立、行走 [2] [3]。韩国Walk on suit机器人可以帮助下肢瘫痪患者实现平地、楼梯、坡道等路况行走 [4]。中科院先进技术研究所运用传感器结合脑电信号研发了一款外骨骼机器人，并对其在线步态规划进行了研究 [5] [6]。上海傅里叶研发的Fourier机器人可应用于辅助截瘫或偏瘫患者行走 [7]。北京大艾机器人研发的AiLegs下肢外骨骼可以运用单步行走的方式辅助患者上下楼梯 [8]。

下肢机器人的步态规划策略主要有以下几种：1) 使用预定义步态控制，预先采集正常人运动步态，将其转化为电机转动角度后，直接控制电机运转。该方法易于实现，但修改数据较为困难，无法适应于不同使用场景 [9] [10]。2) 使用动力学模型规划轨迹，采集机器人工作时的反作用力信息，结合机器人动力学模型，求得机器人运动步态和轨迹。此方法的有效性极大程度上依赖于建立模型的精确性 [11]。3) 使用样条曲线规划轨迹，该方法在确定轨迹关键点(运动始末点、最高点等)后，使用三次样条、五次样条等样条曲线对关键点进行拟合，以获得机器人运动轨迹。该方法生成的曲线较为光滑，但其泛化学习能力较为不足。

动态运动基元(Dynamic Movement Primitives, DMPs)是一种基于模仿学习的机器人轨迹规划方法，其运用一个带有强迫项的弹簧阻尼模型二阶动力系统对初始轨迹进行编码，根据目标点的改变进行轨迹的泛化学习。该方法计算的效率较高，规划的轨迹光滑、连续性好，泛化学习能力强，适合用于不同环境下的机器人轨迹规划 [12]。本文中将运用动态运动基元结合机器人正逆运动学建模，规划适用于不同尺寸楼梯的机器人步态和轨迹。

2. 运动学模型建立与分析

在完成行走、上下楼梯等运动时，下肢运动主要发生在矢状面。因此下肢助行机器人设计过程中，各关节只保留矢状面内的屈伸自由度。下肢助行机器人可以看作是一个五连杆机构，通过关节将一系列连杆连接起来，组成一个运动链。

对下肢助行机器人进行运动学分析，可以有效建立机器人运动状态和各关节电机旋转角度之间的关系，为下肢助行机器人的轨迹规划和步态规划打下基础。

2.1. 改进型D-H模型建立

Denavit和Hartenberg在1955年提出运用参数表达机器人各连杆机构的运动关系 [11] [13]。之后Craig对D-H表示法进行改进，使其更为直观容易理解，本文运用改进型D-H法来描述下肢助行机器人。

下肢助行机器人在一个上楼步态周期内，首先以一条腿作为支撑腿，支撑在第2级台阶上，其踝关节位置相对固定。另一条腿作为摆动腿，从第1级台阶迈向第3级台阶，稳定后，该腿转换为支撑腿。此时第一条腿进入摆动相，从第2级台阶迈向第4级台阶，一个完整步态完成。

在步行楼梯的过程中，人体两腿的运动呈现周期性、对称性，故而可对单腿进行D-H建模。如下图1所示，建立单腿关节坐标系，以足踝关节所在位置为坐标系0，分别建立固连于足踝关节、膝关节和髋关节的坐标系。下肢助行机器人单腿D-H模型参数如下表1所示。其中 $a_i$ 为连杆长度、 ${\alpha }_i$ 为连杆扭角、 $d_i$ 为两连杆距离、 ${\theta }_i$ 表示两连杆夹角、 $l_2$ 表示小腿长度， $l_3$ 表示大腿长度。

Table 1. D-H parameters of a single leg of the lower limb walking-assistant robot

表1. 下肢助行机器人单腿D-H参数

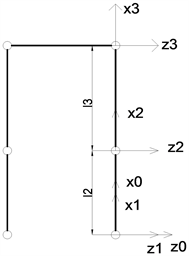
Figure 1. D-H model of the lower limb walking-assistant robot

图1. 下肢助行机器人D-H模型

2.2. 正逆运动学分析

对下肢助行机器人进行运动学分析，将得到机器人运动状态和关节角度之间的关系 [11] [14]。依据机器人D-H模型，下肢助行机器人单腿D-H模型各连杆的变换矩阵如下所示：

${}_1{}^{0}T=\left[\begin{array}{cccc}\cos {\theta }_1& -\sin {\theta }_1& 0& 0\\ \sin {\theta }_1& \cos {\theta }_1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$ (1)

${}_2{}^{1}T=\left[\begin{array}{cccc}\cos {\theta }_2& -\sin {\theta }_2& 0& l_2\\ \sin {\theta }_2& \cos {\theta }_2& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$ (2)

${}_3{}^{2}T=\left[\begin{array}{cccc}\cos {\theta }_3& -\sin {\theta }_3& 0& l_3\\ \sin {\theta }_3& \cos {\theta }_3& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$ (3)

式中， ${}_i{}^{i-1}T$ 表示连杆i相对于连杆i − 1的位姿， ${\theta }_1$ 、 ${\theta }_2$ 、 ${\theta }_3$ 分别为踝关节、膝关节和髋关节运动角度， $l_2$ 为小腿长度， $l_3$ 为大腿长度。

将各变换矩阵相乘，可以得到机器人末端机构相对于基坐标系{0}的位姿：

$\begin{array}{c}{}_3{}^{0}T={}_1{}^{0}T\left({\theta }_1\right){}_2{}^{1}T\left({\theta }_2\right){}_3{}^{2}T\left({\theta }_3\right)\\ =\left[\begin{array}{cccc}\cos \left({\theta }_1+{\theta }_2+{\theta }_3\right)& -\sin \left({\theta }_1+{\theta }_2+{\theta }_3\right)& 0& l_3\cdot \cos \left({\theta }_1+{\theta }_2\right)+l_2\cdot \cos \left({\theta }_1\right)\\ \sin \left({\theta }_1+{\theta }_2+{\theta }_3\right)& \cos \left({\theta }_1+{\theta }_2+{\theta }_3\right)& 0& l_3\cdot \sin \left({\theta }_1+{\theta }_2\right)+l_2\cdot \sin \left({\theta }_1\right)\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$ (4)

上式矩阵中左上角3 × 3的部分表示末端机构在基坐标系中的姿态，第4列前3个元素表示末端机构在基坐标系中的位置。

下肢助行机器人在使用过程中，可以运用传感器和轨迹规划算法获知末端机构的位姿，若要将其转化为电机运转角度就需要对下肢助行机器人进行逆运动学分析。本文将采用代数法进行下肢助行机器人逆运动学分析。

在逆运动学分析前，先对下肢助行机器人做出以下假设：1) 机器人在步行楼梯的过程中，人体的上半身始终保持竖直。2) 步行过程中，下肢助行机器人足底始终与地面保持平行。

将下肢助行机器人的运动方程表示为式5，若末端机构位置和姿态已知，则式中 $\stackrel{\rightharpoonup }{n}$ 、 $\stackrel{\rightharpoonup }{o}$ 、 $\stackrel{\rightharpoonup }{a}$ 、 $\stackrel{\rightharpoonup }{p}$ 均为已知量。

${}_3{}^{0}T=\left[\begin{array}{cc}\begin{array}{cc}{n}_x& o_x\\ n_y& o_y\end{array}& \begin{array}{cc}{a}_x& p_x\\ a_y& p_y\end{array}\\ \begin{array}{cc}{n}_z& o_z\\ 0& 0\end{array}& \begin{array}{cc}{a}_z& p_z\\ 0& 1\end{array}\end{array}\right]={}_1{}^{0}T\left({\theta }_1\right){}_2{}^{1}T\left({\theta }_2\right){}_3{}^{2}T\left({\theta }_3\right)$ (5)

使用逆变换 ${}_1{}^{0}T{}^{-1}\left({\theta }_1\right)$ 左乘式5两侧，得：

${}_1{}^{0}T{}^{-1}\left({\theta }_1\right){}_3{}^{0}T={}_2{}^{1}T\left({\theta }_2\right){}_3{}^{2}T\left({\theta }_3\right)$ (6)

令式6中左右两侧矩阵的第1行第4列和第2行第4列对应元素相等，可以得到下式：

$\{\begin{array}{l}{p}_x\cos {\theta }_1+p_y\sin {\theta }_2=l_2+l_3\cos {\theta }_2\\ p_y\cos {\theta }_1-p_x\sin {\theta }_2=l_3\sin {\theta }_2\end{array}$ (7)

计算可得转角 ${\theta }_2$ 和 ${\theta }_1$ ：

${\theta }_2=\arccos \frac{p_x^2+p_y^2-l_2^2-l_3^2}{2l_2{l}_3}$ (8)

${\theta }_1=\arctan \frac{p_y}{p_x}-\arctan \frac{l_3\sin {\theta }_2}{\sqrt{p_x^2+p_y^2-{\left(l_3\sin {\theta }_2\right)}^2}}$ (9)

由上述假设可知 ${\theta }_3=0-{\theta }_1-{\theta }_2$。

3. 基于改进的动态运动基元的轨迹规划

动态运动基元(Dynamic Movement Primitives)即DMPs，是Stenfan Schaal团队在2002提出的一种运用于机器人和机械臂的轨迹规划的框架 [15] [16] [17] [18]。该方法可以用于表达复杂轨迹，可用于不同使用场景下不同结构机器人的轨迹规划，并且动态运动基元法拥有良好的稳定性和平滑性，参数调整过程也较为便捷。该方法能良好地用于下肢助行机器人的运动轨迹规划，可以通过对预先采集的一条运动步态的模仿学习，规划出适应于不同尺寸楼梯的运动轨迹。

3.1. 动态运动基元原理

动态运动基元(DMPs)用若干弱线性系统表示非线性系统，通过局部加权回归算法对强迫项的权重进行修改。动态运动基元主要分为两类，分别为离散型和周期型。对下肢助行机器人进行轨迹规划时，使用的原始轨迹一般为采集得到的人体运动轨迹，该轨迹是由一系列散点经曲线拟合形成的。因此，本文中使用离散型动态运动基元来规划下肢助行机器人的运动轨迹。

DMPs运用一个二阶弹簧阻尼模型作为基础控制策略，添加强迫项对系统进行调制，使其能稳定趋向于目标值，系统如下所示：

$\{\begin{array}{l}\tau \stackrel{\dot{}}{z}={\alpha }_z\left({\beta }_z\left(g-y\right)-z\right)+f\\ \tau \stackrel{\dot{}}{y}=z\end{array}$ (10)

其中g为目标点， ${\alpha }_z$ 、 ${\beta }_z$ 是常数， $\tau$ 为时间常数，y、 $\stackrel{\dot{}}{y}$ 和 $\ddot{y}$ 是系统目前位置、速度和加速度，f是一个强迫项，式10称为变换系统。

${\alpha }_z$ 、 ${\beta }_z$ 选择适当时，上述系统可以达到临界阻尼状态，此时整个系统将单调收敛于g。若将上式中f表示为非线性函数，那么系统可以用来描述任意复杂曲线。式10中的强迫项f是关于时间的函数，该项的显示时间依赖性将使式10成为一个线性时变动力系统，这样的系统难以与其他动力系统耦合，同一系统中多个自由度也难以协调。通常将引入一个一阶线性动力系统 $\tau \stackrel{\dot{}}{x}=-{\alpha }_{x}x$ 对时间进行替换。

3.2. 改进的动态运动基元原理

本文使用一个二阶正则系统(式11)代替一阶线性动力系统，以使得强迫项f不产生加速度间断，避免初始加速度不连续对系统的影响。

$\{\begin{array}{l}\tau \stackrel{\dot{}}{v}={\alpha }_v\left(-{\beta }_{v}x-v\right)\\ \tau \stackrel{\dot{}}{x}=v\end{array}$ (11)

其中， ${\alpha }_v$ 、 ${\beta }_v$ 是常数，x可以看作相位变量，x和v在运动开始时均为0，当系统到达目标g时，x和v返回0。式11称为规范系统。

选择适当常数，使系统呈现临界阻尼状态，强迫项f则可以定义为式12，

$f\left(x\right)=\frac{{\displaystyle {\sum }_{i=1}^N{\Psi }_i\left(x\right){\omega }_i}}{{\displaystyle {\sum }_{i=1}^N{\Psi }_i\left(x\right)}}v\left(g-y_0\right)$ (12)

${\Psi }_i=\exp \left(-\frac{1}{2{\sigma }_i^2}{\left(x-c_i\right)}^2\right)$ (13)

其中， ${\Psi }_i$ 为指数基函数， ${\sigma }_i$ 为基函数带宽， $c_i$ 是基函数中心， $y_0$ 为系统初始状态， ${\omega }_i$ 为可调权重。式12含有N个基函数，当达到目标g时，强迫项f将消失，因此可以证明式10具有良好的稳定性。

为了保证系统状态y可以在运动结束时收敛于目标点g，在强迫项f前添加一个门控项u。门控项作为一个衰减系统，在变换系统中y值接近目标g的过程中，u将从1变化到0。门控系统如式14所示：

$u=\frac{1}{1+{\text{e}}^t}$ (14)

当目标值g变化时，式10中的加速度项将产生一个不连续的跳跃，为了使系统速度变化更加平滑，对目标值的变化进行限制，如式15：

$\tau \stackrel{\dot{}}{g}={\alpha }_g\left(g_0-g\right)$ (15)

DMPs具有良好的稳定性，在对轨迹进行放缩后，轨迹本身的属性将被保留，维持其原始的运动方向和趋势。动态运动基元使用监督学习的方法拟合适合于不同原始轨迹的权重 ${\omega }_i$。调整式10的顺序，并将原始轨迹的示教信息带入，得到式16。

$f_{\text{target}}={\tau }^2{\ddot{y}}_{\text{demo}}-{\alpha }_z\left({\beta }_z\left(g-y_{\text{demo}}\right)-\tau {\ddot{y}}_{\text{demo}}\right)$ (16)

运用局部加权回归方法计算f中每一个 ${\Psi }_i$ 对应的 ${\omega }_i$，使得其局部加权二次标准误差最小，如下式：

$J_i={\displaystyle {\sum }_{t=i}^P{\Psi }_i\left(t\right){\left(u\cdot f_{\text{target}}\left(t\right)-{\omega }_i\xi \left(t\right)\right)}^2}$ (17)

其中 $\xi \left(t\right)=v\left(t\right)\left(g-y_0\right)$。解得 ${\omega }_i$ ：

${\omega }_i=\frac{S^{\text{T}}{\Gamma }_i{f}_{\text{target}}}{S^{\text{T}}{\Gamma }_{i}S}$ (18)

其中，

$S=\left(\begin{array}{c}\xi \left(1\right)\\ \xi \left(2\right)\\ ⋮\\ \xi \left(P\right)\end{array}\right)$， ${\Gamma }_i=\left(\begin{array}{cccc}{\Psi }_i\left(1\right)& & & 0\\ & {\Psi }_i\left(2\right)& & \\ & & \ddots & \\ 0& & & {\Psi }_i\left(P\right)\end{array}\right)$，

$f_{\text{target}}=\left(\begin{array}{c}u\left(1\right)\cdot f_{\text{target}}\left(1\right)\\ u\left(2\right)\cdot f_{\text{target}}\left(2\right)\\ ⋮\\ u\left(P\right)\cdot f_{\text{target}}(\; P\; )\end{array}\right)$

4. 仿真验证

本节使用matlab仿真验证DMPs结合运动学分析规划步态的效果。首先使用DMPs模仿原始运动轨迹，再根据楼梯参数规划新的关节运动轨迹，最后运用逆运动学分析得到各关节运动角度，完成助行机器人步态规划。

4.1. DMPs轨迹规划仿真验证

根据上文中的分析，人体步行楼梯的运动主要发生在矢状面，因此可以将人体运动过程在三维空间中的信息转化为二维，即只考虑人体在x轴和y轴方向的运动。分别对下肢助行机器人的腰部髋关节和摆动腿踝关节运动轨迹进行规划，选取相同的时间尺度，可以分别获得髋关节和摆动腿踝关节在x和y方向上关于时间的轨迹曲线。

基于DMPs的轨迹规划步骤主要分为：1) 设置初始化参数，如表2所示。2) 将一条正常人上楼梯的运动轨迹作为原始轨迹输入。3) 根据式16计算强迫项f，并根据式13计算每个高斯核函数。4) 根据式17和式18计算每个核函数的权重 ${\omega }_i$。5) 依据设定的目标位置g，根据式10计算新轨迹的加速度，对加速度求积分后获得轨迹曲线的速度和位置。

Table 2. DMPs parameter table

表2. DMPs参数表

以上楼梯时摆动腿踝关节运动轨迹规划为例，将初始运动曲线分解为x和y两个方向分别关于时间的一维曲线。此一维曲线为示教曲线，运用DMPs模仿该曲线的形状和趋势，将曲线的特征以参数的形式保存下来。根据楼梯参数修改轨迹末端目标点g，DMPs依照原始曲线的特征，重新规划适合新楼梯的运动轨迹。

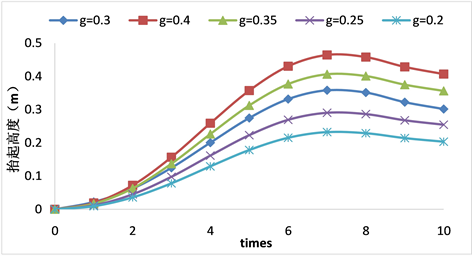
Figure 2. Swing leg vertical movement curve of ankle joint

图2. 摆动腿踝关节竖直方向运动曲线

图2为经过DMPs规划后，不同楼梯高度下摆动腿踝关节竖直方向各时刻位置。以摆动腿踝关节运动起始点为原点，横轴为时间，纵轴为踝关节各时刻的抬起高度。其中，曲线g = 0.3为原始轨迹曲线，其余为根据不同楼梯高度规划所得新曲线，目标点g为楼梯高度的2倍。由图中可以看出，运用动态运动基元方法规划轨迹，能够保持原始轨迹的形状特征，同时准确收敛于目标点。

以相同的时间尺度规划摆动腿踝关节在水平方向的运动轨迹，目标点设置为楼梯宽度的2倍。图3为摆动腿踝关节在人体矢状面内的运动轨迹曲线，坐标原点为运动起始点，横坐标为摆动腿踝关节在水平方向上的位移，纵坐标为踝关节在竖直方向上的位移。

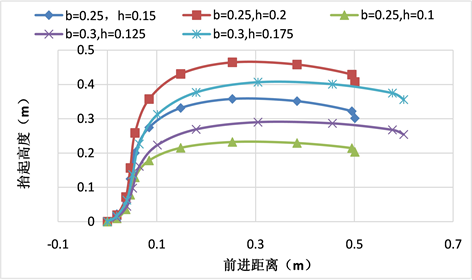
Figure 3. Motion curve in sagittal plane of swinging ankle joint

图3. 摆动提踝关节矢状面内运动曲线

由图3可以看出，使用相同时间参数进行轨迹规划可以有效协调机器人多个自由度之间的运动。使用表2中的参数，规划机器人摆动腿踝关节在水平方向上的运动轨迹，将其与踝关节竖直方向上的轨迹曲线相结合，可以得到摆动腿踝关节的实际运动曲线。图中楼梯宽度b = 0.25 m，高度h = 0.15 m的曲线为原始曲线，其余曲线为DMPs依据不同楼梯尺寸规划所得。机器人不同自由度运动曲线相结合，得到机器人矢状面内运动的二维曲线，该曲线也将保持原始曲线的形状和趋势。

经由改进型DMPs规划的关节运动轨迹，曲线平滑、连续，没有间断点。轨迹曲线收敛性好，能准确达到目标点，可以保证机器人实际运行中能达到所需位置。使用改进型DMPs规划的运动轨迹与原始轨迹的形状和运动趋势基本相似，保留了原始示教曲线的特点，能够保证机器人的步态符合人体运动特点。

4.2. 机器人步态规划仿真验证

DMPs规划得到新的运动轨迹后，运用逆运动学分析，可以把运动轨迹转化为助行机器人运动时各关节所需角度。

图4验证了本文中逆运动学分析的准确性。图4(a)为真实上楼梯时膝关节运动角度，图4(b)楼梯尺寸相同的情况下，逆运动学求解后得到的机器人膝关节运动角度。可以看出，两条曲线的形状和运动趋势基本相同，验证了本文中运动学分析的准确性。

图5为根据不同楼梯尺寸规划所得机器人膝关节运动角度。图中楼梯宽度b = 0.25 m，楼梯高度h = 0.15 m的曲线为原始曲线，其余曲线为以该原始曲线为参考曲线规划所得。可以看出规划得到的曲线很大程度上保留了源曲线的趋势和形状，说明规划所得的运动角度基本符合人体运动，DMPs结合逆运动学分析能够有效地规划助行机器人运动的步态。

(a) 原始膝关节运动角度 (b) 逆运动学解得膝关节运动角度

Figure 4. Simulation verification of inverse kinematics gait planning

图4. 逆运动学步态规划的仿真验证

Figure 5. Validation of the gait plan under different staircase parameters

图5. 不同楼梯参数下步态规划的验证

5. 结论

为了解决下肢助行机器人辅助使用者步行不同尺寸楼梯的问题，本文运用动态运动基元算法结合机器人运动学分析，规划关节运动轨迹并计算各关节运动角度。本文的工作内容及创新点如下：首先，对下肢助行机器人进行D-H建模，对其进行运动学分析，建立末端机构位姿与各关节角度的关系。获取一组人体步行楼梯的数据，将其作为初始轨迹，再运用改进后的动态运动基元对其进行模拟。依据楼梯高度和宽度参数，调整DMPs算法中目标点，规划出适应于不同尺寸楼梯的下肢助行机器人踝关节和髋关节运动轨迹。最后，使用规划出的新轨迹进行机器人逆运动分析，获得各关节运动角度。本文中改进DMPs规划的曲线平滑、连续、收敛性好，能够模仿人体运动轨迹特点，结合运动学分析，可以有效运用于下肢助行机器人轨迹规划。

基金项目

上海市产业协同创新项目(2021-cyxt1-kj07)，上海市市级科技重大专项(2021SHZDZX)，上海介入医疗器械工程技术研究中心(18DZ2250900)。