1. 引言
平面直边无孔多边形父子关系判断是空间拓扑关系的一项重要的内容,有着诸多重要的应用,技术和方法比较成熟有效。但目前国内基本都依赖于国外的各种第三方组件,对于其原理的理解尚为黑盒状态。即使有部分相关文献的发表,其最终的实现效果尚无法覆盖全部场景。
目前,工程上应用最多的还是射线法,但其应用场景也仅局限在了简单多边形间的父子关系判断上。
本文研究的内容将在简单多边形间的父子关系判断之上,进一步探讨复杂的凹凸多边形间的父子关系判断的算法,最终得到的算法将同样适用于简单多边形间的父子关系判断。
2. 平面直边无孔多边形父子关系判断的常用方法及其存在的主要问题
从技术上讲,这样的问题很早就得到了解决,而且在很多文献中都对此有所介绍,但从目前公开的文献中看,绝大多数仅是从实现上做了大概的介绍。比如文献 [1],其所提供的算法,仅能应用于特定场景,无法满足全场景的判断。文献 [2],其所提供的算法过于复杂,计算量太大,且仅针对简单多边形,覆盖场景不全。而文献 [3] 和文献 [4] 虽然提供的算法简单,但同样也只能针对简单多边形间的父子关系做判断,针对复杂的凹凸多边形就无法适用了。例如,使用文献 [1]、文献 [2]、文献 [3]、文献 [4] 的算法针对图二中的所有关系进行判断时,总是有一些判断结果与事实不服。
本文介绍的基于射线法的平面无孔直边多边形父子关系判断算法。它是为满足“上海西门子医疗器械有限公司MES系统”的工厂建模地图绘制功能而设计的。
全场景大致分为三类,一类是普通平面直边无孔多边形间的父子关系判断,一类是普通平面直边无孔多边形于异形平面直边无孔多边形间的父子关系判断,一类是异形平面直边无孔多边形间的父子关系判断。
本文的算法很好的完成了全场景的判断,本文采用纯数学的方法实现,该算法自动化程度高、运行高效、场景覆盖面广,具有很强的使用价值。
3. 基于射线法的平面直边无孔多边形父子关系判断算法
3.1. 基本目的
二维直边多边形的父子关系冲突判断,通常的做法是,判断子多边形是否有点在父多边形外。但这种方法覆盖的场景并不全面,因为存在满足以上条件但仍然冲突的场景。如下图1所示:
除此之外整个平面直边无孔多边形父子关系判断还有其它场景,如下图2所示:
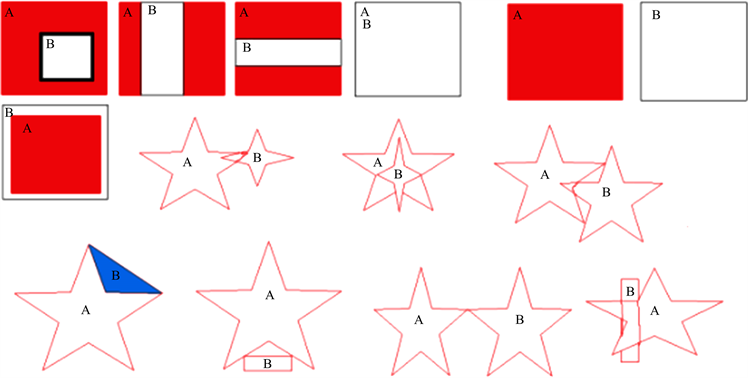
Figure 2. Polygonal parent-child relationship determination scenario
图2. 多边形父子关系判断场景
本算法的目的是满足图1及图2中的所有场景中的平面直边无孔多边形间的父子关系判断。
3.2. 基本算法
该算法需要两个要素:组成多边形的顶点的集合,组成多边形的直线段的集合。只有组成多边形的线段的端点与组成多边形的定点重合且组成多边形的线段是直的,才是符合要求的。
从以上图1和图2可知,平面直边无孔多边形的父子关系判断的三个关键点:
1) 子多边形的点全部在父多边形内。
2) 父多边形的点全部在子多边形外。
3) 父多边形的线段与子多边形的线段不交叉。
3.3. 算法的详细说明及实现
3.3.1. 创建多边形
定义一个代表多边形类,此类包含两个属性。
属性:
1) Points:当前多边形的所有端点的集合。
2) LineSagements:基于Points组成当前多边形的线段的集合。
代码见附录1
3.3.2. 创建点
定义一个代表点的类,此类仅包含两个double类型的属性X、Y。
其中X为点的X坐标,Y为点的Y坐标。
代码见附录2
3.3.3. 创建线段
定义一个代表线段的类型,此类包含5个属性、1个方法。
属性:
1) Start:线段的起始点。
2) End:线段的终止点。
3) FunType:线段的类型。
4) Params:double类型的列表,线段的斜率及线段与Y轴的交点。当列表中的第一个对象代表当前线段的斜率,第二个对象代表当前线段与Y轴的交点的Y坐标;其中当列表中仅存在一个对象时,表示当前线段与Y轴不相交。
5) Intersection:与其它线段的交点列表。
方法:
6) GetFuncParam:求当前线段的斜率,并设置当前线段的类型,当当前线段为斜线时,同时求出当前线段与Y轴的交点的Y坐标。
注意:须在构造线段对象的同时,调用GetFuncParam方法。
代码见附录3
3.3.4. 创建线段类型的枚举
枚举类型如下:
1) XX:竖线
2) YY:横线
3) XnXYnY:斜线
代码见附录4
3.3.5. 创建点与线的关系的枚举
枚举类型如下:
1) VertexOverlap:顶点重合
2) Cross:相交
3) UnCross:不相交
4) OnLineSagement:点在线上
代码见附录5
3.3.6. 在多边形类中增加冲突检测方法CheckIfInArea
该方法的入参为父多边形对象,返回值为true或者false,其中true代表这两个多边形的父子关系成立,false则代表这两个多边形的父子关系不成立。
方法体如下:
1) 若父多边形的LineSagements为空,则当前方法返回true。
2) 循环当前多边形的Points中的对象,使用循环出的对象,调用其自身的CheckIfInArea方法,将父多边形传入这个方法,并对调用的返回结果取反,若取反后的结果为true,则当前方法返回false。
3) 循环父多边形的Points中的对象,使用循环出的对象,调用其自身的CheckIfInArea方法,将当前多边形传入这个方法,若返回的结果为true,则当前方法返回false。
4) 调用当前多边形对象的WhetherPolygonIntersection方法,并将父多边形传入这个方法,若返回结果为false,则当前方法返回true;若返回结果为false,则判断当前多边形的线段是否有在父多边形外的部分。
判断方法如下:
1) 循环取当前多边形的LineSagements中的对象,赋值给临时变量edg。
2) 判断edg的交点列表中是否存在对象。若存在对象则执行下一步,否则进行下一次循环。
3) 判断edg的类型,若为竖线则进行第4步,若为横线则进行第5步,若为斜线则进行第6步。
4) 将edg的交点列表按照每个交点的Y坐标进行升序,然后赋值给临时变量jiaodianList;循环取jiaodainList中的元素,赋值给临时变量start,取下一个元素赋值给临时变量end,创建一个新的点对象,赋值给临时变量z,其中z的X坐标为start的X坐标,z的Y坐标为start的Y坐标加上end的Y坐标减去start的Y坐标的差的1/2;
使用z调用其自身的CheckIfInArea方法,将父多边形传入该方法,然后判断返回结果,若返回结果为true则跳过本次循环,直接进行下一次,若返回结果为false,则当前方法返回false。
5) 将edg的交点列表按照每个交点的X坐标进行升序,然后赋值给临时变量jiaodianList;循环取jiaodainList中的元素,赋值给临时变量start,取下一个元素赋值给临时变量end,创建一个新的点对象,赋值给临时变量z,其中z的X坐标为start的X坐标加上end的X坐标减去start的X坐标的差的1/2;
z的Y坐标为start的Y坐标;
使用z调用其自身的CheckIfInArea方法,将父多边形传入该方法,然后判断返回结果,若返回结果为true则跳过本次循环,直接进行下一次,若返回结果为false,则当前方法返回false。
6) 判断edg的起始点的Y坐标是否小于等于edg的终止点的Y坐标,若是则进行第7步,若不是则进行第8步。
7) 将edg的交点列表先按照每个交点的X坐标进行升序,然后按照每个交点的Y坐标升序,然后赋值给临时变量jiaodianList;循环取jiaodainList中的元素,赋值给临时变量start,取下一个元素赋值给临时变量end,创建一个新的点对象,赋值给临时变量z,其中z的X坐标为start的X坐标加上end的X坐标减去start的X坐标的差的1/2 (公式2);
使用z调用其自身的CheckIfInArea方法,将父多边形传入该方法,然后判断返回结果,若返回结果为true则跳过本次循环,直接进行下一次,若返回结果为false,则当前方法返回false。
8) 将edg的交点列表先按照每个交点的X坐标进行升序,然后按照每个交点的Y坐标降序,然后赋值给临时变量jiaodianList;循环取jiaodainList中的元素,赋值给临时变量start,取下一个元素赋值给临时变量end,创建一个新的点对象,赋值给临时变量z,其中z的X坐标为start的X坐标加上end的X坐标减去start的X坐标的差的1/2 (公式2);
使用z调用其自身的CheckIfInArea方法,将父多边形传入该方法,然后判断返回结果,若返回结果为true则跳过本次循环,直接进行下一次,若返回结果为false,则当前方法返回false。
代码见附录6
3.3.7. 在点的类中增加点与线段关系的判断方法CheckPointInLineSagement
该方法的入参为需要与之判断的线段,返回值为当前点与传入线段的关系。主要功能是判断此点向右引出的射线是否穿过传入的线段。
穿过的定义如下:
1) 此点在传入线段的顶点上。
2) 此点在传入线段的线上。
3) 此点不符合以上两种情况,且此点向右引出的射线与传入的线段有交点。
方法主体如下:
1) 判断此点是否在传入线段的顶点上,若是,则返回关系VertexOverlap (顶点重合)。否则进行下一步
2) 判断传入线段的类型。
若为竖线:
判断此点的X坐标是否等于传入线段的起始点的X坐标;且此点的Y坐标是否小于等于传入线段的起始点的Y坐标且此点的Y坐标大于等于传入线段的终止点的Y坐标,或者此点的Y坐标大于等于传入线段的起始点的Y坐标且此点的Y坐标小于等于传入线段的终止点的Y坐标。若是,则此方法返回关系OnLineSagement (点在线上)。
若为横线:
判断此点的y坐标是否等于传入线段的起始点的y坐标;且此点的x坐标是否大于等于传入线段的起始点的x坐标且此点的X坐标小于等于传入线段的终止点的X坐标,或者此点的X坐标小于等于传入线段的起始点的X坐标且此点的X坐标大于等于传入线段的终止点的X坐标。若是,则此方法返回关系OnLineSagement (点在线上)。
若为斜线:
则进行第3步
3) 判断传入线段的起始点的Y坐标是否小于此点的Y坐标且传入线段的终止点的y坐标大于等于此点的Y坐标;或者,传入线段的起始点的Y坐标大于等于此点的y坐标且传入线段的终止点的Y坐标小于此点的y坐标。若不是则进行第4步。否则需要先求出传入线段与射线Y坐标相同的点的X坐标,然后将这个X坐标与当前点的x坐标进行比较,以判断当前点与传入线段的关系。
若交点的X坐标等于当前点的x坐标,则返回关系OnLineSagement (点在线上),否则判断交点的x坐标是否大于当前点的x坐标,若是则返回关系Cross (相交),否则进行第4步。
交点的X坐标为:
t.Y:当前点的Y坐标
rs.X:传入线段的起始点的X坐标
rs.Y:传入线段的起始点的Y坐标
rz.X:传入线段的终止点的X坐标
rz.Y:传入线段的终止点的Y坐标
4) 返回关系UnCross (不相交)。
代码见附录7
3.3.8. 在点的类中增加子多边形的点是否在父多边形内的判断方法CheckIfInArea
该方法的入参为父多边形,返回值为true或者false,其中true代表当前点在传入的多边形内(包含当前点与传入多边形的顶点重合的情况) flse代表当前点在传入的多边形外。
方法主体如下:
1) 定义临时变量射线穿过传入多边形边界的次数cnt,并赋值为0。
2) 循环取传入多边形的LineSagements中的元素,判断其类型,若为Cross类型则将cnt的值+1。若为OnLineSagement类型,则返回true。若为VertexOverlap类型则返回true。若为UnCross类型则进行下一次循环。
3) 判断cnt是否为奇数,若为奇数则返回true。否则返回false。
代码见附录8
3.3.9. 在点的类中增加父多边形的点是否在子多边形内的判断方法CheckIfInChildArea
该方法的入参为子多边形,返回值为true或者false,其中true代表当前点在传入的多边形内(包含当前点与传入多边形的顶点重合的情况),flse代表当前点在传入的多边形外。
方法主体如下:
1) 定义临时变量射线穿过传入多边形边界的次数cnt,并赋值为0。
2) 循环取传入多边形的LineSagements中的元素,判断其类型,若为Cross类型则将cnt的值+1。若为OnLineSagement类型,则返回false。若为VertexOverlap类型则返回false。若为UnCross类型则进行下一次循环。
3) 判断cnt是否为奇数,若为奇数则返回true。否则返回false。
代码见附录9
3.3.10. 在多边形的类中增加多边形自身的线段是否与另一多边形的所有线段相交的方法WhetherPolygonIntersection
该方法的入参为多边形,返回值为true或者false,其中true代表当前多边形的线段与传入多边形中的线段有相交的情况,false代表当前多边形的线段与传入多边形中的线段没有相交的情况。
方法主体如下:
1) 循环取当前多边形的线段,赋值给临时变量edg。
2) 将edg的起始点赋值给临时变量a。
3) 将edg的终止点赋值给临时变量b。
4) 循环取传入多边形的线段,赋值给临时变量fatherEdge。
5) 将fatherEdge的起始点赋值给临时变量c。
6) 将fatherEdge的终止点赋值给临时变量d。
7) 定义临时变量denominator。
8) 求denominator的值。
9) 判断denominator是否等于0,若不等于0则进行第32步,否则进行下一步。
10) 判断edg的类型,若为竖线,则进行第11步,若为横线,则进行第18步,若为斜线,则进行第25步。
11) 判断edg的起始点的X坐标是否等于fatherEdge的起始点的X坐标,若不是则跳出当前循环,进行下一次循环。若是则进行下一步。
12) 判断b的Y坐标是否大于c的Y坐标或者a的Y坐标是否小于d的Y坐标。若是则跳出当前循环,进行下一次循环。
13) 判断a的Y坐标是否等于c的Y坐标并且b的Y坐标是否等于d的Y坐标。若是则跳出当前循环,进行下一次循环。
14) 判断a的Y坐标是否大于c的Y坐标并且b的Y坐标小于等于c的Y坐标并且b的Y坐标大于等于d的Y坐标。若是则将c加入到edg的Intersection中,然后跳出当前循环,进行下一次循环。
15) 判断a的坐标是否小于等于c的Y坐标并且a的Y坐标大于等于d的Y坐标并且b的Y坐标小于d的Y坐标。若是则将d加入到edg的Intersection中,然后跳出当前循环,进行下一次循环。
16) 判断c的Y坐标是否大于等于a的Y坐标且d的Y坐标小于等于b的Y坐标。若是则跳出当前循环,进行下一次循环。
17) 判断a的Y坐标是否大于等于c的Y坐标并且b的Y坐标小于等于d的Y坐标。若是则将c和d加入edge的Intersection中。然后跳出当前循环,进行下一次循环。
18) 判断edg的起始点的Y坐标是否等于fatherEdge的起始点的Y坐标。若不是则跳出当前循环,进行下一次循环。否则进行下一步。
19) 判断b的X坐标是否小于c的X坐标或者a的X坐标大于d的X坐标。若是则跳出当前循环,进行下一次循环。
20) 判断a的X坐标是否等于c的X坐标且b的X坐标等于d的X坐标。若是则跳出当前循环,进行下一次循环。
21) 判断a的X坐标是否小于c的X坐标并且b的X坐标大于等于c的X坐标并且b的X坐标小于等于d的X坐标。若是则将c加入edg的Intersection中,然后跳出当前循环,进行下一次循环。
22) 判断b的X坐标是否大于d的X坐标并且a的X坐标大于等于c的X坐标并且a的X坐标小于等于d的X坐标。若是则将d加入edg的Intersection中,然后跳出当前循环,进行下一次循环。
23) 判断c的X坐标是否小于等于a的X坐标并且d的X坐标大于等于b的X坐标。若是则跳出当前循环,进行下一次循环。
24) 判断a的X坐标是否小于等于c的X坐标并且b的X坐标大于等于d的X坐标。若是则将c和d加入edg的Intersection中,然后跳出当前循环,进行下一次循环。
25) 判断edg的斜率是否等于fatherEdge的斜率并且edg与Y轴交点的Y坐标等于fatherEdge与Y轴交点的Y坐标。若不是则跳出当前循环,进行下一次循环。否则进行下一步。
26) 判断a的X坐标是否小于c的X坐标并且b的X坐标小于c的X坐标或者判断a的X坐标是否大于d的X坐标并且b的X坐标大于d的X坐标。若是则跳出当前循环,进行下一次循环。
27) 判断a的X坐标是等于c的X坐标并且a的Y坐标等于c的Y坐标并且b的X坐标等于d的X坐标并且b的Y坐标等于d的Y坐标。若是则跳出当前循环,进行下一次循环。
28) 判断a的X坐标是否小于c的X坐标并且b的X坐标大于等于c的X坐标并且b的X坐标小于等于d的X坐标。若是则将c加入edg的Intersection中,然后跳出当前循环,进行下一次循环。
29) 判断a的X坐标是否大于等于c的X坐标并且a的X坐标小于等于d的X坐标并且b的X坐标大于d的X坐标。若是则将d加入edg的Intersection中,然后跳出当前循环,进行下一次循环。
30) 判断a的X坐标是否大于等于c的X坐标并且a的X坐标小于等于d的X坐标并且b的X坐标大于等于c的X坐标并且b的X坐标小于等于d的X坐标。若是则跳出当前循环,进行下一次循环。
31) 判断a的X坐标是否小于等于c的X坐标并且b的X坐标大于等于d的X坐标。若是则将c和d加入edg的Intersection中,然后跳出当前循环,进行下一次循环。
32) 定义线段所在直线的交点坐标x
33) 定义线段所在直线的交点坐标y
34) 判断以下两个公式的结果是否都小于等于0,若是则将线段所在直线的交点加入edg的Intersection中,若不是则跳出当前循环,进行下一次循环。
35) 循环结束后,判断当前多边形的LineSagements中是否包含Intersection中包含元素的元素,若是则返回true,否则返回false。
代码见附录10
4. 结论
本文提出的算法,只需要按顺序提供需要进行判断的两个平面直边无孔多边形的顶点的坐标,即可通过本文的算法判断出他们之间的父子关系是否成立。本文给出的算法相较文献 [1]、文献 [2]、文献 [3]、文献 [4],其处理流程更加清晰,覆盖场景更加全面,编码简单,易于实现,无编程语言限制,代码复用率高,且只要是平面直边无孔多边形,不论是简单多边形还是凹、凸多边形,均可正确判断出它们之间的父子关系是否成立。
该算法用于“上海西门子医疗器械有限公司MES系统”工厂建模地图绘制中,满足了区域地图规划,验证了该算法的可行性。
致谢
致谢本文的算法得到了在上海西门子医疗器械有限公司任职的陈勍齐的大力支持与论证,在此表示衷心的感谢!
附录
附录1
publicclass Area
{
public Area(List< Point > points)
{
Points = points;
if(this.Points !=null&&this.Points.Any())
{
LineSagements =new List< LineSagement >();
for(int i =0; i < points.Count -1; i++)
{
LineSagements.Add(new LineSagement(points[i], points[i +1]));
}
LineSagements.Add(new LineSagement(points.First(), points.Last()));
}
}
public List< Point > Points {get;set;}
public List< LineSagement > LineSagements {get;set;}
}
附录2
publicclass Point
{
public Point(double x,double y)
{
this.X = x;
this.Y = y;
}
publicdouble X {get;privateset;}
publicdouble Y {get;privateset;}
}
附录3
publicclass LineSagement
{
public LineSagement(Point start, Point end)
{
this.Start = start;
this.End = end;
GetFuncParam(this);
}
public Point Start {get;privateset;}
public Point End {get;privateset;}
public LineType_Enum FunType {get;set;}
public List< double > Params {get;set;}=new List< double >();
/// < summary >
/// 交点列表
/// < /summary >
public List
Intersection {get;set;}=new List< Point >();
publicvoid GetFuncParam(LineSagement lineSegment)
{
double x1 =this.Start.X;
double y1 =this.Start.Y;
double x2 =this.End.X;
double y2 =this.End.Y;
if(x1 == x2)
{
//type=2
this.FunType = LineType_Enum.XX;
this.Params.Add(x1);
}
elseif(y1 == y2)
{
//type=1
this.FunType = LineType_Enum.YY;
this.Params.Add(y1);
}
else
{
//type=3
this.FunType = LineType_Enum.XnXYnY;
double a =(y2 - y1)/(x2 - x1);//斜率
double b = y1 -(x1 *((y2 - y1)/(x2 - x1)));//与Y轴的交点
this.Params.Add(a);
this.Params.Add(b);
}
}
}
附录4
publicenum LineType_Enum
{
/// < summary >
/// 竖线
/// < /summary >
XX,
/// < summary >
/// 横线
/// < /summary >
YY,
/// < summary >
/// 斜线
/// < /summary >
XnXYnY
}
附录5
publicenum PointWithLineSagementState_Enum
{
/// < summary >
/// 顶点重合
/// < /summary >
VertexOverlap,
/// < summary >
/// 相交
/// < /summary >
Cross,
/// < summary >
/// 不相交
/// < /summary >
UnCross,
/// < summary >
/// 在线段上
/// < /summary >
OnLineSagement
}
附录6
publicbool CheckIfInArea(Area area)
{
if(area.LineSagements ==null)
{
returntrue;
}
//若子点有在父外的则结束
foreach(Point point inthis.Points)
{
if(!point.CheckIfInArea(area))
returnfalse;
}
//若父点有在子内的则结束
foreach(Point point in area.Points)
{
if(point.CheckIfInChildArea(this))
returnfalse;
}
//所有子线段与父线段没有相交则不冲突
if(WhetherPolygonIntersection(area))
{
foreach(LineSagement edg inthis.LineSagements)
{
if(edg.Intersection.Any())
{
if(edg.FunType == LineType_Enum.XX)
{
List< Point > jiaodainList = edg.Intersection.OrderBy(m => m.Y).ToList();
for(int i =0; i < jiaodainList.Count -1; i++)
{
Point start = jiaodainList[i];
Point end = jiaodainList[i +1];
Point z =new Point(start.X, start.Y +((end.Y - start.Y)/2));
if(z.CheckIfInArea(area))
{
continue;
}
else
{
returnfalse;
}
}
}
elseif(edg.FunType == LineType_Enum.YY)
{
List< Point > jiaodainList = edg.Intersection.OrderBy(m => m.X).ToList();
for(int i =0; i < jiaodainList.Count -1; i++)
{
Point start = jiaodainList[i];
Point end = jiaodainList[i +1];
Point z =new Point(start.X +((end.X - start.X)/2), start.Y);
if(z.CheckIfInArea(area))
{
continue;
}
else
{
returnfalse;
}
}
}
elseif(edg.FunType == LineType_Enum.XnXYnY)
{
if(edg.Start.Y <= edg.End.Y)
{
List< Point > jiaodainList = edg.Intersection.OrderBy(m => m.X).ThenBy(m => m.Y).ToList();
for(int i =0; i < jiaodainList.Count -1; i++)
{
Point start = jiaodainList[i];
Point end = jiaodainList[i +1];
Point z =new Point(start.X +((end.X - start.X)/2), start.Y +((end.Y - start.Y)/2));
if(z.CheckIfInArea(area))
{
continue;
}
else
{
returnfalse;
}
}
}
else
{
List< Point > jiaodainList = edg.Intersection.OrderBy(m => m.X).ThenByDescending(m => m.Y).ToList();
for(int i =0; i < jiaodainList.Count -1; i++)
{
Point start = jiaodainList[i];
Point end = jiaodainList[i +1];
Point z =new Point(start.X +((end.X - start.X)/2), start.Y -((start.Y - end.Y)/2));
if(z.CheckIfInArea(area))
{
continue;
}
else
{
returnfalse;
}
}
}
}
}
}
}
else
{
returntrue;
}
returntrue;
}
附录7
public PointWithLineSagementState_EnumCheckPointInLineSagement(LineSagement sagement)
{
double px =this.X;
double py =this.Y;
//bool flag = false;
Point pi = sagement.Start;
Point pj = sagement.End;
double sx = pi.X;double sy = pi.Y;
double tx = pj.X;double ty = pj.Y;
//点与线段顶点重合
bool psTf =(px == sx && py == sy);
bool ptTf =(px == tx && py == ty);
if(psTf || ptTf)
{
return PointWithLineSagementState_Enum.VertexOverlap;
}
switch(sagement.FunType)
{
case LineType_Enum.XX:
if(px == pi.X &&((py <= sy && py >= ty)||(py >= sy && py <= ty)))
return PointWithLineSagementState_Enum.OnLineSagement;
break;
case LineType_Enum.YY:
if(py == pi.Y &&((px >= sx && px <= tx)||(px <= sx && px >= tx)))
return PointWithLineSagementState_Enum.OnLineSagement;
break;
case LineType_Enum.XnXYnY:
default:
break;
}
//判断线段端点是否在射线两侧
if((sy < py && ty >= py)||(sy >= py && ty < py))
{
//线段上与射线Y坐标相同的点的X坐标
double x = sx +(py - sy)*(tx - sx)/(ty - sy);
//点在线段上
if(x == px)
{
return PointWithLineSagementState_Enum.OnLineSagement;
}
//射线穿过线段
if(x > px)
{
return PointWithLineSagementState_Enum.Cross;
}
}
return PointWithLineSagementState_Enum.UnCross;}
附录8
publicbool CheckIfInArea(Area theArea)
{
int cnt =0;
foreach(LineSagement lineSagement in theArea.LineSagements)
{
switch(CheckPointInLineSagement(lineSagement))
{
case PointWithLineSagementState_Enum.Cross:
cnt +=1;
break;
case PointWithLineSagementState_Enum.OnLineSagement:
returntrue;
case PointWithLineSagementState_Enum.VertexOverlap:
returntrue;
case PointWithLineSagementState_Enum.UnCross:
default:
break;
}
}
//射线穿过多边形边界的次数为奇数时点在多边形内
if(cnt %2==1)
{
returntrue;//点在多边形内
}
else
{
returnfalse;//点不在多边形内
}
}
附录9
publicbool CheckIfInChildArea(Area theArea)
{
int cnt =0;
foreach(LineSagement lineSagement in theArea.LineSagements)
{
switch(CheckPointInLineSagement(lineSagement))
{
case PointWithLineSagementState_Enum.Cross:
cnt +=1;
break;
case PointWithLineSagementState_Enum.OnLineSagement:
returnfalse;
case PointWithLineSagementState_Enum.VertexOverlap:
returnfalse;
case PointWithLineSagementState_Enum.UnCross:
default:
break;
}
}
//射线穿过多边形边界的次数为奇数时点在多边形内
if(cnt %2==1)
{
returntrue;//点在多边形内
}
else
{
returnfalse;//点不在多边形内
}
}
附录10
public bool WhetherPolygonIntersection(Area father)
{
List< LineSagement > childEdgeXfatherEdge_List =new List< LineSagement >();
foreach(LineSagement edg inthis.LineSagements)
{
Point a = edg.Start;
Point b = edg.End;
foreach(LineSagement fatherEdge in father.LineSagements)
{
Point c = fatherEdge.Start;
Point d = fatherEdge.End;
double denominator =(b.Y - a.Y)*(d.X - c.X)-(a.X - b.X)*(c.Y - d.Y);
// 如果分母为0 则平行或共线, 不相交
if(denominator ==0)
{
//竖线
if(edg.FunType == LineType_Enum.XX)
{
//共线
if(edg.Start.X == fatherEdge.Start.X)
{
//不重叠
if(b.Y > c.Y || a.Y < d.Y)
{
continue;
}
//完全重叠
if(a.Y == c.Y && b.Y == d.Y)
{
continue;
}
//上跨立(包含两线相接)
if(a.Y > c.Y && b.Y <= c.Y && b.Y >= d.Y)
{
edg.Intersection.Add(c);
continue;
}
//下跨立(包含两线相接)
if(a.Y <= c.Y && a.Y >= d.Y && b.Y < d.Y)
{
edg.Intersection.Add(d);
continue;
}
//父包子
if(c.Y >= a.Y && d.Y <= b.Y)
{
continue;
}
//子包父
if(a.Y >= c.Y && b.Y <= d.Y)
{
edg.Intersection.Add(c);
edg.Intersection.Add(d);
continue;
}
}
//平行
else
{
continue;
}
}
//横线
elseif(edg.FunType == LineType_Enum.YY)
{
//共线
if(edg.Start.Y == fatherEdge.Start.Y)
{
//不重叠
if(b.X < c.X || a.X > d.X)
{
continue;
}
//完全重叠
if(a.X == c.X && b.X == d.X)
{
continue;
}
//左跨立(包含两线相接)
if(a.X < c.X && b.X >= c.X && b.X <= d.X)
{
edg.Intersection.Add(c);
continue;
}
//右跨立(包含两线相接)
if(b.X > d.X && a.X >= c.X && a.X <= d.X)
{
edg.Intersection.Add(d);
continue;
}
//父包子
if(c.X <= a.X && d.X >= b.X)
{
continue;
}
//子包父
if(a.X <= c.X && b.X >= d.X)
{
edg.Intersection.Add(c);
edg.Intersection.Add(d);
continue;
}
}
//平行
else
{
continue;
}
}
//斜线
elseif(edg.FunType == LineType_Enum.XnXYnY)
{
//共线
if(edg.Params.First().Equals(fatherEdge.Params.First())&& edg.Params.Last().Equals(fatherEdge.Params.Last()))
{
//不重叠
if((a.X < c.X && b.X < c.X)
||(a.X > d.X && b.X > d.X))
{
continue;
}
//完全重叠
if(a.X == c.X && a.Y == c.Y && b.X == d.X && b.Y == d.Y)
{
continue;
}
//跨立(包含两线相接)
if(a.X < c.X && b.X >= c.X && b.X <= d.X)
{
edg.Intersection.Add(c);
continue;
}
//跨立(包含两线相接)
if(a.X >= c.X && a.X <= d.X && b.X > d.X)
{
edg.Intersection.Add(d);
continue;
}
//父包子
if(a.X >= c.X && a.X <= d.X && b.X >= c.X && b.X <= d.X)
{
continue;
}
//子包父
if(a.X <= c.X && b.X >= d.X)
{
edg.Intersection.Add(c);
edg.Intersection.Add(d);
continue;
}
}
//平行
else
{
continue;
}
}
}
// 线段所在直线的交点坐标 (x , y)
double x =((b.X - a.X)*(d.X - c.X)*(c.Y - a.Y)
+(b.Y - a.Y)*(d.X - c.X)* a.X
-(d.Y - c.Y)*(b.X - a.X)* c.X)/ denominator;
double y =-((b.Y - a.Y)*(d.Y - c.Y)*(c.X - a.X)
+(b.X - a.X)*(d.Y - c.Y)* a.Y
-(d.X - c.X)*(b.Y - a.Y)* c.Y)/ denominator;
// 判断交点是否在两条线段上
if(
// 交点在线段1上
(x - a.X)*(x - b.X)<=0&&(y - a.Y)*(y - b.Y)<=0
// 且交点也在线段2上
&&(x - c.X)*(x - d.X)<=0&&(y - c.Y)*(y - d.Y)<=0)
{
edg.Intersection.Add(new Point(x, y));
}
else
{
continue;
}
}
}
if(this.LineSagements.Where(m => m.Intersection.Any()).Any())
{
returntrue;
}
else
{
returnfalse;
}
}