1. 绪论
1.1. 研究背景和意义
1.1.1. 研究背景
我国的国民经济中有非常多的重要支柱产业,汽车是其中非常重要的产业之一,它承担了推动社会发展的重要责任,对于我国的经济发展同时也有着很强的带动作用。近几年来,我国经济进入稳步递增的阶段,汽车产销迅速发展,国内汽车保有量和销量得到非常大的提升,到2018年,我国汽车的生产量和销售量到已是连续10年赠联全球第一 [1]。由于我国的汽车市场形态发生了非常大的变化,已经赶超国际汽车营销的步伐。当消费者购买汽车可以满足自己的需求,并且意识到汽车带来的利益,同时认为购买汽车是满足需要的理想途径,购买汽车感到满足之后,汽车企业可以获得成功。因此研究汽车购买决策并分析影响因素,能够帮助汽车企业作出明确的营销决策,制定正确的营销策略,同时也能帮助消费者自身作出更明智的购买决策。
1.1.2. 研究意义
本文切合当前社会发展要求,以社会热点汽车为研究对象,运用UCI机器学习数据库中的1728条消费者对于汽车购买意愿的评价数据集,通过多类别Logistic回归方法建立模型来探究影响消费者对汽车购买意愿的诸多因素 [2],从而了解和掌握汽车潜在消费者的特征,以及得到影响消费者购买意愿的关键因素,另外本文还通过多类别Logistic回归方法建立模型对汽车前景进行分析和预测。本文通过分析验证得出消费者对汽车接受度以及影响消费者购买意愿关键因素的结论。从生产厂商以及销售者的角度,让生产厂商和销售者准确了解消费者关键诉求,从而有针对性地提升服务,提高产品质量,更准确得进行市场推广。使企业进一步认识到影响消费者决策行为的因素,为汽车企业今后在更加精确的市场细分中进行汽车设计、生产、定价、营销等活动,提供一定的借鉴。从消费者角度,为消费者提供适当的引导以及为有计划购买汽车的消费者提供参考。
1.2. 文章内容结构简介
本文共分为五个部分,具体内容如下:
第一部分为绪论,主要介绍文章的研究背景,叙述了论文在理论和实践方面的主要研究意义。
第二部分为基本方法与模型介绍,主要叙述了本文所用的主要方法和模型,包括广义线性模型、多类别Logistic模型以及其评估方法。
第三部分为数据说明。通过机器学习数据库找到汽车评价数据集,并对数据集中的指标作出说明和解释,为后续建立数学模型做准备。
第四部分为数据分析及实证结果。针对数据集进行实证分析,利用Spearman等级相关系数检验汽车的基本特征与消费者购买意愿的相关性,采用多项有序Logistic回归模型进行建模,并运用混淆矩阵对模型进行评估。
第五部分为研究结论和局限性。根据实证分析结果,得到影响购消费者买汽车的主要因素,并提出文章存在的不足之处。
2. 理论基础
2.1. 广义线性模型
一般的线性回归模型只能对数据进行线性关系的建模。为了更好得反映数据间的非线性关系,广义线性模型(GLM)得以提出 [3]。它运用联结函数建立起输出变量的条件期望与输入变量的线性组合之间的非线性关系。通过变换联结函数的表达式,使得所建立的模型能够映现多种输出变量与输入变量间的非线性关系,这是线性模型在统计实践中发展的产物。假设
是输出变量
的n个独立观测,均服从指数族分布,即
有概率密度函数:
(1)
其中为为
的自然参数,参数
为尺度参数,与具体的i值无关,函数
是
参数
的函数,
是
和
的函数。
为对应于
的p维输入变量
的n个观测值。记
,其中
为未知参数向量。假设
,并且
和
具有关系:
(2)
称此定义的模型为广义线性模型。其中函数
称为联结函数。
2.2. Logistic回归模型
Logistic回归是一种广义线性回归 [4],与多重线性回归分析有很多相同之处。它们的模型形式基本上相同。Logistic回归分析用于研究X对Y的影响,并且对X的数据类型没有要求,X可以为定类数据,也可以为定量数据,但要求Y必须为定类数据,并且根据Y的选项数,使用相应的数据分析方法。一般可分为3类,分别是二元Logistic回归分析、多分类Logistic回归分析和有序Logistic回归分析。
其中当定性因变量Y取两个类别时即为二元Logistic回归,二元逻辑斯蒂回归模型的表达式是一个条件概率分布
,这里的
为输入变量,输出变量
关于X的条件分布是伯努利分布,取值为0或者1,我们通过如下的定义具体表达
(3)
当定性因变量Y取k个类别时,记为
,因变量Y取值于每个类别的概率与一自变量
有关,对于样本数据
, 多类别Logistic回归模型第i组样本的因变量
取第个类别的概率为
(4)
有序Logistic回归即定性因变量Y有多个选项,并且各选项之间可以对比大小。
2.3. 模型评估方法
2.3.1. 混淆矩阵
根据Logistic回归得到的模型其因变量是多元数据,通常在对模型进行评估时可以以混淆矩阵为基础来评价因变量估计结果的准确性。对二元数据,以0.5为分类阈值(预测结果小于0.5,则default为0,否则default为1),将预测值与训练集中的实际default进行比较,得到的混淆矩阵(见表1)。
采用预测精度,预测准确率,错误类型一以及错误类型二的方式对模型进行评级。其中:
(5)
(6)
2.3.2. 伪判定系数R2
伪判定系数R2用于衡量回归模型相比于默认模型在解释数据时的效果,其值应该小于1,若值大于1,则得到的回归模型就不能被信任,数据集就不适合采用逻辑回归算法进行分类预测。
伪判定系数R2定义为
(7)
其中
是空模型的偏差,
是回归模型的偏差。
3. 数据说明
本文数据是UCI机器学习数据库的汽车评价数据,数据资源来自于http://archive.ics.uci.edu/ml/。该数据集总共包括七个变量,其中购买意愿为因变量,剩余六个自变量分别为购入费用,维修费用,内部空间,安全性,座位数;该数据总共包含1728条样本记录。本文所使用的数据分析工具主要是R语言 [5]。首先,描述顾客对汽车购买意愿Y包含四种水平,不被接受(unacc)、偶有接受(acc)、较为接受(good)、很受欢迎(Vgood),按程度由低到高依次记为0、1、2、3。具体6个自变量见表2。
4. 实证分析
4.1. 数据分析
4.1.1. 描述性统计
将汽车评价数据作为基础数据集(见表3),总样本数为1728个。对于因变量Y (购买意愿)而言,分类属性为0即不被接受的频数为1210,占比70.02%;分类属性为1即偶有接受的频数为384,占比22.22%;分类属性为2即较为接受的频数为69,占比3.99%;分类属性为3即很受欢迎的频数为65,占比仅为3.76%,数据分布不太均匀。

Table 3. Frequency distribution of dependent variables analyzed by ordered Logistic regression
表3. 有序Logistic回归分析因变量频数分布
4.1.2. 变量相关性分析
首先对变量间相关关系进行探究,由于较多变量为分类型变量,因此采用Spearman相关系数,调用程序包corrplot进行分析得到相关系数图(见图1),通过图1我们可以看到因变量Y即购车意愿与X1 (购入费用)、X2 (维修费用)的Spearman相关系数分别为−0.24和−0.21,均为负相关;与其余自变量的Spearman相关系数均为正数,同时与X6 (安全性)的相关系数最高,达到了0.47。
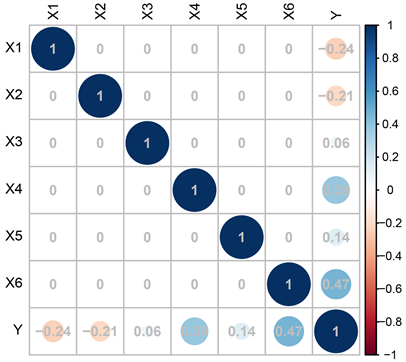
Figure 1. Spearman correlation coefficient diagram of variables
图1. 变量的Spearman相关系数图
另外,回归分析一般假设建模变量之间都是独立不相关的,如果有任何两个变量存在强相关性,则只需保留其中一个而删除其余变量。通过将建模指标中存在明显相关的指标进行筛选剔除,使得所有自变量都不显著相关,避免自变量之间存在很强的共线性而导致模型效果不好。自变量间的Kappa系数均小于100,存在较弱的多重共线性,表明6个评级指标都适合作为消费者对汽车接受程度的自变量来建立数学模型。
4.2. 数据建模
4.2.1. 模型似然比检验
从表4可知:此处模型检验的原定假设为:是否放入自变量(X1, X2, X3, X4, X5, X6)两种情况时模型质量均一样;分析显示拒绝原假设(chi = 1335.270, p = 0.000 < 0.05),即说明本次构建模型时,放入的自变量具有有效性,本次模型构建有意义。

Table 4. Likelihood ratio test of ordered Logistic regression model
表4. 有序Logistic回归模型似然比检验
4.2.2. 建模结果
因为数据中的因变量购买意愿为四项有序的分类变量,因此我对数据构建多项有序logistic回归进行分析,利用R软件中的MASS包中的“polr”函数进行建模 [6],代码如下:
model1=polr(as.factor(Class.Values)~buying+maint+doors+persons+lug_boot+safety, method='logistic', Hess=T, data=CARdata)
summary(model1)
由于R软件 [7] 中“polr”函数构建的多项有序logistic回归模型没有变量系数的显著性检验项,因此利用如下代码“p <- pnorm(abs(ctable[, t value]), lower.tail = FALSE) * 2”计算系数项的P值,并利用如下代码“exp(coef(model1))”计算自变量的优势比(OR值)。
最终分析结果见表5:

Table 5. Results of multiple ordered Logistic regression
表5. 多项有序Logistic回归结果
注:0代表因变量中不被接受(unacc);1代表因变量中偶有接受(acc);2代表因变量中较为接受(good)。

Table 6. Odds Ratio of each variable (OR value)
表6. 各自变量优势比(OR值)
从表5我们可以看出,模型伪R平方值(McFadden R方)为0.462,意味着X1,X2,X3,X4,X5,X6可以解释Y的46.2%变化原因;以及模型公式如下:
结合表5各变量优势比值(见表6),我们可以得出,X1的回归系数值为−1.208,并且呈现出0.01水平的显著性(z = −15.937, p = 0.000 < 0.01),意味着X1会对Y产生显著的负向影响关系。以及优势比(OR值)为0.299,意味着X1增加一个单位时,Y的变化(减少)幅度为0.299倍;
X2的回归系数值为−1.019,并且呈现出0.01水平的显著性(z = −14.158, p = 0.000 < 0.01),意味着X2会对Y产生显著的负向影响关系。以及优势比(OR值)为0.361,意味着X2增加一个单位时,Y的变化(减少)幅度为0.361倍;
X3的回归系数值为0.276,并且呈现出0.01水平的显著性(z = 4.415, p = 0.000 < 0.01),意味着X3会对Y产生显著的正向影响关系。以及优势比(OR值)为1.317,意味着X3增加一个单位时,Y的变化(增加)幅度为1.317倍;
X4的回归系数值为1.078,并且呈现出0.01水平的显著性(z = 18.630, p = 0.000 < 0.01),意味着X4会对Y产生显著的正向影响关系。以及优势比(OR值)为2.940,意味着X4增加一个单位时,Y的变化(增加)幅度为2.940倍;
X5的回归系数值为0.917,并且呈现出0.01水平的显著性(z = 10.101, p = 0.000 < 0.01),意味着X5会对Y产生显著的正向影响关系。以及优势比(OR值)为2.501,意味着X5增加一个单位时,Y的变化(增加)幅度为2.501倍;
X6的回归系数值为2.743,并且呈现出0.01水平的显著性(z = 20.724, p = 0.000 < 0.01),意味着X6会对Y产生显著的正向影响关系。以及优势比(OR值)为15.531,意味着X6增加一个单位时,Y的变化(增加)幅度为15.531倍;总结分析可知:X3,X4,X5,X6共4项会对Y产生显著的正向影响关系,以及X1,X2共2项会对Y产生显著的负向影响关系。
4.3. 模型预测与评估
将数据集的前70%的数据划分为训练集,后30%的数据划分为测试集,利用前面所构建的有序logistic模型进行预测,预测代码为“mean(predicted.classes == test_data$Y)”,得到训练集上总的平均预测准确度为0.815,通过R里面的caret程序包中confusionMatrix函数分别构建混淆矩阵用于模型评估 [8]。
我们可以计算得出在混淆矩阵中测试集因变量总的预测准确度和四个类别各自的预测准确度(见表7)。
测试集总的预测准确度:(344 + 65 + 0 + 14)/519 = 0.815
0 (unacc)的预测准确度:344/(344 + 33) = 0.912
1 (acc):的预测准确度:65/(36 + 65 + 3) = 0.625
2 (good):的预测准确度:0/17 = 0.000
3 (Vgood):的预测准确度:14/(7 + 14) = 0.667
可以得出在整个测试集的预测精度还比较好,但是对于类别2 (good)由于它的样本数量较少,预测准确度较低。

Table 7. Confusion matrix of ordered Logistic regression model
表7. 有序Logistic回归模型的混淆矩阵
通过表8可以得出,整体的预测准确率为0.815,95%置信区间为(0.779, 0.848),同时麦克尼马检验的p值为0 [9],表明在统计上是显著的,另外R软件中confusion Matrix函数对于测试集上通过七种统计量给出因变量四种类别的预测准确度加以对比,不同的预测统计量给出的预测准确率有所不同,但是可以发现在类别为Class: 0 (unacc)和Class: 3 (Vgood)的各项准确率较高,其余两项类别中准确率较差;最终的平均预测率中,Class: 0 (unacc)和Class: 3 (Vgood)的预测准确率分别为0.830和0.829,Class: 1 (acc)为0.746,Class: 2 (good)准确率最差仅为0.499。
5. 研究结论与局限性
5.1. 研究结论
通过构建四分类有序Logistic回归模型进行建模预测后发现:首先购入费用和维修费用对消费者汽车购买意愿有显著的负向影响,车门数、座位数、内部空间、安全性对消费者汽车购买意愿有显著的正向影响;购入费用的优势比(OR值)为0.299,意味着它增加一个单位时,购买意愿的变化(减少)幅度为0.299倍;维修费用优势比(OR值)为0.361,意味着它增加一个单位时,购买意愿的变化(减少)幅度为0.361倍。而安全性这个自变量对消费者汽车购买意愿的影响最大,同时其优势比(OR值)为15.531,意味着安全性增加一个单位时,购买意愿的变化(增加)幅度为15.531倍,这表明样本数据中消费者更加注重安全性,其实车企制造商要注重汽车安全性能,同时可以提高购车优惠;其次,利用构建的有序Logistic回归模型对测试集数据(后30%)进行预测时,对整体预测准确率达到了0.815,在现实生活中,在对具体类别进行预测时部分效果不尽人意。
本文通过构建多项有序Logistic回归进行研究,研究探究了与汽车直接相关的影响因素对于购买决策的重要性,证实了汽车安全性成为消费者在进行家用汽车购买决策中的重要的衡量指标。这就要求对于汽车生产企业在汽车制造上面需要更加注重安全性。
5.2. 研究的局限性
本文存在如下几个不足之处:一、由于数据的限制,在对购车意愿的影响因素进行探究时只挑选了数据集中仅有的六个变量,在实际生活中购车意愿可能受其他重要因素影响,因此可能遗漏了重要变量;二、数据集的数量仅有一千余条,数据量偏少,在划分测试集后,部分类别样本数仅为十几条,这可能是某些类别最后的预测准确度不够理想的部分原因;三、在做分类预测时更好的做法是采用几种不同的分类模型加以对比,以看出有序Logistic回归模型在本次分类中是否为最优选择。