渤海湾蓬莱19-3油田漏油问题的仿真与决策

Simulation and Decision of Oil Leakage Problem in Penglai 19-3 Oilfield, Bohai Bay

摘要: 蓬莱19-3油田漏油事故严重影响了海洋经济与生态发展，海洋保护问题再一次成为社会热点话题。本文首先针对渤海石油泄漏的问题，借助物理中受力分析和流体力学控制方程，分别考虑在平静海平面上、受到自身重力和某种外在因素影响、受到洋流和风力影响下油膜状态，并利用计算机MATLAB程序仿真建立了溢油扩散的数学模型，反映溢油的扩散规律。其次，利用几何图形模拟实际场景，分析上述三种情况下的漏油点的确定方法。最后进行最优决策，确定需要建立的最佳监测点位置及个数，将溢油对海洋生态的损失降到最低。

Abstract: The oil leakage accident in Penglai 19-3 oilfield has seriously affected the Marine economy and ecological development, the Marine protection issue has once again become a hot topic in society. This paper first addresses the problem of oil leakage in Bohai Sea, with the help of physical force analysis and hydrodynamic control equations, respectively considers the oil membrane state at the calm sea level, under its own gravity and some external factors, under the ocean current and wind influence. The mathematical model of oil spill diffusion is established by using computer MATLAB program and reflects the diffusion law of the oil spill. Secondly, the geometry is used to simulate the actual scene and analyze the determination method of oil leakage points in the above three scenarios. Finally, the optimal decision is made to determine the optimal location and number of monitoring points to be established, so as to minimize the loss of oil spill to Marine ecology.

1. 研究背景

随着科学的进步，海洋石油资源的开发和利用已经成为未来经济发展的必然选择，海上石油开采活动日益频繁，海上石油运输也日趋活跃。然而一旦发生重大漏油、溢油事件，不但开采公司将面临巨大的经济损失，海湾的生态环境也将面临灭顶之灾。以2011年蓬莱19-3油田泄漏事故为例(如图1所示)，由于溢油扩散，蓬莱19-3油田溢油事故对整个渤海生态系统如海水、海底沉积物、浮游生物、底栖动物等都有很大破坏，其损害难以估量且大多数不可逆转，对渔业、旅游业、生态环境以及人类生命安全都产生了极大的恶劣影响。截止至今，海上溢油事故的相关数据越来越多，人们逐渐从多方面考虑降低溢油损失的方法，其中最为重要的一步就是根据已有数据对溢油进行数值模拟，建立合适的模型进行分析。随着计算机的迅速更新，研究人员将模型从一维变换到三维，考虑的影响因素、研究目的、研究内容等也更具备综合性。目前溢油模型的建立主要从动力过程和非动力过程两个角度出发，已经逐步趋于完善。 但对于实际情况下海洋石油最佳监测点位置和个数的确定研究较少。本文依据2021年辽宁省数学建模竞赛B题和现有研究对于墨西哥湾原油泄漏事件的模型分析，分多种情况综合探究利用计算机建模工具仿真模拟蓬莱19-3油田溢油事故海上溢油的扩散影响因素以及扩散规律，并与实际溢油扩散形态进行粗略比对，进一步说明模型建立的可行性。不仅如此，本文就如何确定最佳监测点设置个数和监测点的最佳地理位置监测漏油情况这一问题进行优化决策，以达到节约成本，减少人力物力的目的，将漏油风险损失降到最低，具有深刻的现实意义。

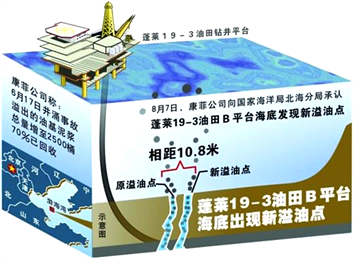
Figure 1. Penglai 19-3 oilfield leakage accident

图1. 蓬莱19-3油田泄漏事故

2. 溢油扩散的仿真模型建立

2.1. 溢油问题分析

考虑溢油的蒸发、乳化、生物降解对油膜扩散的影响，石油在溢入海洋之后，在海洋特定的环境下，将会进行比较复杂的物理、化学、生物变化，如乳化、氧化、蒸发、扩散，自然风化以及微生物缓慢降解等，如图2所示。在蒸发过程中，溢油在海面上扩散时有很大的一部分暴露在表面，溢油中的可挥发成分迅速挥发，产生损失并由液态变为气态。随着溢油扩展不断进行，会发生乳化。溢油与海水在风、潮流及波浪的共同作用下不断混合，最终形成油包水或水包油的油水乳化物，长期漂浮在海面上。生物降解将水体中某些维生物以石油中的部分组成部分作为自己的食物和能量来源，在此过程中，达到分解石油的作用。

由此可见，研究溢油扩散问题相当复杂，影响溢油扩散的因素比较多，有自然因素如气候、溢油的自然变化、海水在不同时间段的涨落潮等，也有人为因素如人类活动、船舶停靠等。在建立数学模型时，本文选取影响较大、具有研究价值的因素予以考虑，对于其它影响较小的因素，往往忽略不计。

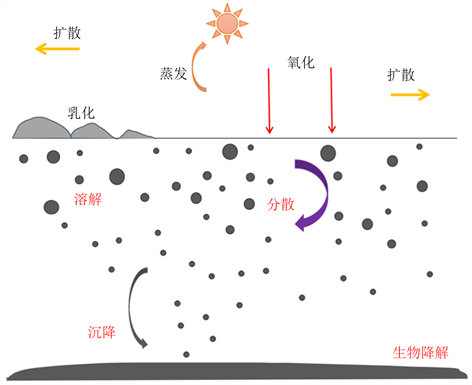
Figure 2. Changing process of offshore oil spill

图2. 海上溢油的迁移变化过程

2.2. 平静海平面上的油膜扩散模型

在不考虑天气等因素时，即在平静的海面，海水各向同性，忽略原油挥发等因素，原油在海水中是以漏油点为中心扩散的，此时假设油膜扩散形状是以漏油点为圆心的圆。

油膜扩散面积与重力加速度、漏油速度、时间等因素有关。首先分析油膜在海面的受力，共有四个力的作用：重力、惯性力、粘滞力、表面张力。根据流体力学控制方程，得到这四个力的表达式如下(见参考文献 [1] )：

重力：

$G=\left({\rho }_s-{\rho }_0\right)g\frac{h}{2}\frac{\partial h}{\partial r}\Delta r$, (1)

惯性力：

$F_1={\rho }_{0}h\frac{\partial u}{\partial t}\Delta r+{\rho }_{0}u\frac{\partial \left(hu\right)}{\partial r}\Delta r$, (2)

表面张力：

$F_2=\frac{1}{2}{K}_1\frac{\partial h}{\partial r}\Delta r$, (3)

粘滞力：

$F_2={\rho }_s{K}_2\frac{2u}{h}\frac{\partial h}{\partial r}\Delta r$. (4)

其中 ${\rho }_s$ 为海水密度，单位为kg/m³； ${\rho }_0$ 为原油密度，单位为kg/m³；g为重力加速度，单位为N/kg，h为油膜平均厚度，单位为m；r为油膜扩展半径，单位为m； $\Delta r$ 为油膜任意时刻运动的微小油段，单位为m；t为溢油时间，单位为天； $K_1$ 为扩张系数； $K_2$ 为海水的粘滞系数；u油膜边缘速度，单位为m/s。

绘制油膜边缘受力示意图，如图3所示。

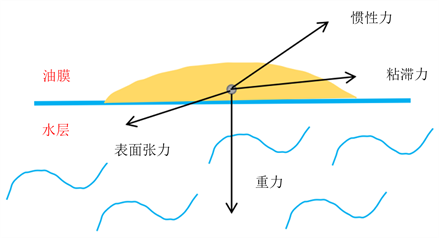
Figure 3. Schematic diagram of stress of oil membrane edge

图3. 油膜边缘受力示意图

经分析，油膜在刚开始形成时自身重力占主导，油膜的一部分重力势能转化为动能，使得油膜在海面上开始扩散，油膜流动受到惯性力和粘滞力的阻碍，其中惯性力起主导地位，所以该阶段可以简化为只受重力和惯性力控制。

于是有

${\rho }_{0}u\frac{\partial \left(h-u\right)}{\partial r}=\left({\rho }_s-{\rho }_0\right)g\frac{h}{2}\frac{\partial h}{\partial r}$. (5)

油膜的平均厚度可以表示为

$D=\frac{V}{\pi r^2}=\frac{Qt}{\pi r^2}$.(6)

油膜边缘的运动速度为

$u=\frac{\text{d}r}{\text{d}t}$. (7)

将以上数据带入得

$r=K_1{\left(1-\frac{\delta }{1-\delta }gQ\right)}^{\frac{1}{4}}{t}^{\frac{3}{4}}$. (8)

其中 $\delta =1-\frac{{\rho }_0}{{\rho }_s}$。

经查阅资料(见参考文献 [2] )得到原油密度 ${\rho }_0=949.3\text{kg}/{\text{m}}^{\text{3}}$，海水密度 ${\rho }_s=1025\text{kg}/{\text{m}}^{\text{3}}$， $g=9.80\text{N}/\text{kg}$，漏油速度 $Q=0.000553\text{m}/\text{s}$，相应数据带入(7)得

$r=1.14\times {\left(\left(\frac{1-\frac{949.3}{1025}}{1-\left(1-\frac{949.3}{1025}\right)}\right)\times 9.80\times 0.000553\right)}^{\frac{1}{4}}{t}^{\frac{3}{4}}=0.1643t^{\frac{3}{4}}$. (9)

由此可见，扩散半径与Q漏油速度和t溢油时间有非线性的关系，并且呈正相关。

又因为油膜扩散形状是以漏油点为圆心的圆，因此油膜扩散面符合圆的面积公式：

$S=\pi r^2$,(10)

将(8)带入到(9)中，最后可以得到油膜扩散面积与扩散时间的函数关系

$S=\pi {\left(0.1643t^{\frac{3}{4}}\right)}^2$. (11)

用MATLAB画出油膜扩散面积S关于时间t的函数图像，如图4。

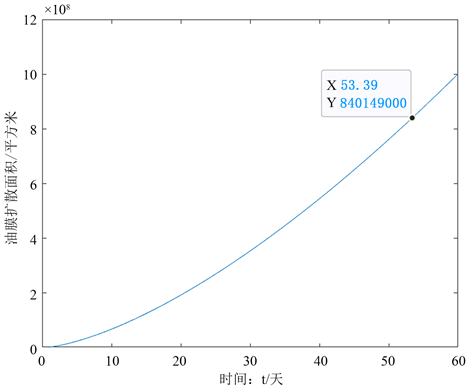
Figure 4. Regular diagram of diffusion area of oil film

图4. 油膜扩散面积规律图

由此，我们清晰地得出了60天内的油膜的扩散规律：油膜扩散面积–时间图像，在此模型的情况假设条件下，我们发现油膜扩散面积只与时间有关，且油膜的扩散面积与时间呈正相关，时间越长，油膜的扩散面积越大，这与实际情况相符合。

为更加直观的看出不同时间内油膜的扩散程度，下面建立极坐标下油膜扩散图(见参考文献 [3] )。

在平静海面上，以漏油点为原点，向东建立x轴方向，向北建立y轴方向，建立xOy平面直角坐标系。

列出油膜扩散圆面参数方程：

$\{\begin{array}{l}x=r\cos \theta \\ y=r\sin \theta \end{array}$,(12)

将(8)代入到(10)中，得到

$\{\begin{array}{l}x=0.1643{\left(86400t\right)}^{\frac{3}{4}}\cos \theta \\ y=0.1643{\left(86400t\right)}^{\frac{3}{4}}\sin \theta \end{array}$, (13)

当漏油天数为1天时，即t = 1带入到(11)中，得

$\{\begin{array}{l}x=0.1643{\left(86400\right)}^{\frac{3}{4}}\cos \theta \\ y=0.1643{\left(86400\right)}^{\frac{3}{4}}\sin \theta \end{array}$. (14)

用MATLAB程序仿真出当t = 1时，油膜的扩散图，如图5。

Figure 5. Oil membrane diffusion plot when t = 1 (Reduce the drawing by 10 times)

图5. 当t = 1时油膜扩散图(将图形缩小10倍)

当漏油天数为60天时，即t = 60带入到(11)中，得

$\{\begin{array}{l}x=0.1643{\left(86400\times 60\right)}^{\frac{3}{4}}\cos \theta \\ y=0.1643{\left(86400\times 60\right)}^{\frac{3}{4}}\sin \theta \end{array}$. (15)

用MATLAB画出当t = 60时，油膜的扩散图，如图6。

Figure 6. Oil membrane diffusion plot when t = 60 (Reduce the drawing by 10 times)

图6. 当t = 60时油膜扩散图(将图形缩小10倍)

由此进一步验证了油膜扩散面积的扩散规律，在平静的海面，只考虑原油的扩散的情况下，随着时间的增加，油膜扩散面积越来越大，越靠近漏油点溢油越多，并且是以漏油点为圆心，向外扩散，形成的油膜边缘呈圆形。

2.3. 受到自身重力和某种外在因素影响的向下的油膜扩散模型

在海洋中，溢油的扩散主要可以分为水平方向和垂直方向，现考虑溢油受到自身重力和某种外在因素影响的向下的扩散，则油膜在x轴和y轴的扩散尺度受到影响而不同。

据查阅资料(见参考文献 [4] )，此时沿x方向得扩散尺度为 $\Delta x=t^{1.17}$， $\Delta y=a{t}^{1.17}$，a一般取 $\frac{1}{\sqrt{10}}$， $\Delta x,\Delta y$

以米为单位，由在情况一得情况下溢油扩展范围为等时圆面，为简化此种情况的计算，此处应用简化公式求圆面面积

$S={10}^5{\left(Qt\right)}^{\frac{3}{4}}$, (16)

此时圆的直径为

$D=\sqrt{\frac{4\times {10}^5{\left(Qt\right)}^{\frac{3}{4}}}{\pi }}$, (17)

所以在该圆得基础上改变 $x,y$ 方向上的扩散尺度，可以得到溢油受向下扩散的影响下扩散轮廓近似呈椭圆，此时有椭圆的参数方程为

$\{\begin{array}{l}x=\frac{{10}^{-3}}{2}\left(\sqrt{\frac{4\times {10}^5{\left(Qt\right)}^{\frac{3}{4}}}{\pi }+{10}^{-3}{t}^{1.17}}\right)\cos \alpha \\ y=\frac{{10}^{-3}}{2}\left(\sqrt{\frac{4\times {10}^5{\left(Qt\right)}^{\frac{3}{4}}}{\pi }+{10}^{-\frac{7}{2}}{t}^{1.17}}\right)\sin \alpha \end{array}\left(0\le \alpha \le 2\pi \right)$. (18)

据此，建立x-y-t模型，用MATLAB程序仿真模拟画出时间——油膜轮廓三维变化图和等时线下油膜平面扩散图，如图7、图8。

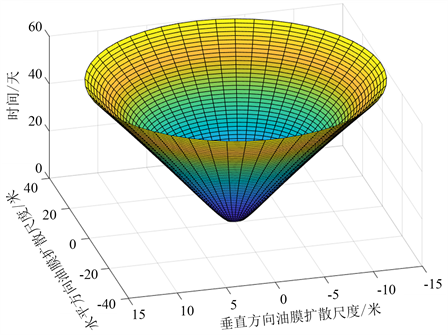
Figure7. 3D variation diagram of time-oil membrane profile

图7. 时间–油膜轮廓三维变化图

该图直观反应了时间的变化对油膜沿x方向和y方向的扩散的影响，可以发现油膜呈椭圆形扩散，且随着时间的增加，扩散面积越来越大。

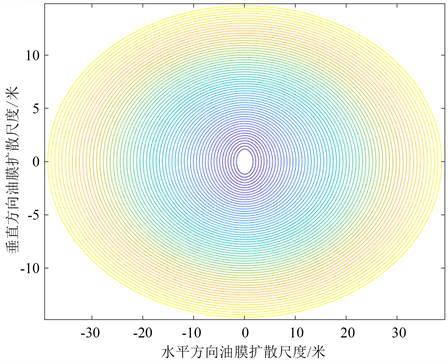
Figure 8. Plane diffusion diagram of the oil film under the isochrony

图8. 等时线下油膜平面扩散图

该图表示在某一时刻，横向观察油膜的扩散形状以及不同位置的溢油量。通过观察，容易发现，溢油受到自身重力和某种外在因素影响下时，扩散形状为椭圆形，从开始溢油到该时刻，以溢油点为中心，向外扩散，油膜自圆心向外厚度逐渐变薄。

2.4. 考虑洋流和风力影响下的石油扩散

考虑洋流，风力对油膜扩散的影响，如图9所示渤海泄露点附近的洋流既有西北方向和东南方向(见参考文献 [5] )，而风向大多为西北风。故而将此情况分为两类1) 洋流方向为西北方向，风向为西北方向，此时洋流与风向同向。2) 洋流方向为西北方向，风向为东南方向，此时洋流与风向反向。两种情况分别根据风力因子与潮流因子得到水风合速度，进而可以建立出油膜位移与时间的关系的数学模型。

Figure 9. Bohai ocean current map

图9. 渤海洋流图

考虑洋流和风力对油膜扩散的影响，设风速为 $v_1$，洋流速度为 $v_2$，风速和洋流速度的合速度为v，则有 $v=\lambda v_1+\mu v_2$，其中 $\lambda$ 为风力因子， $\mu$ 为洋流因子，通过查阅资料，我们得知 $\lambda =0.035$， $\mu =0.6$。以漏油点为原点，向东建立x轴方向，向北建立y轴方向，建立xOy平面直角坐标系。将油膜看成微小的的油膜粒子所组成，设每个油膜粒子的坐标为 $\left(x,y\right)$，油膜粒子的速度u的方向与x轴正方向夹角为 $\alpha$，油膜粒子水风合速度方向v与x轴正方向夹角为 $\beta$，经过时间t后，油膜粒子的位置为 $\left(x+v_{x}t,y+v_{y}t\right)$，因此有参数方程

$\{\begin{array}{l}x=vt\cos \beta +ut\cos \alpha \\ y=vt\sin \beta +ut\sin \alpha \end{array}\left(0\le \alpha \le 2\pi ,0\le \beta \le 2\pi \right)$.(19)

经查阅资料，得到风向为西北风，风速为10 m/s，代入数据得

当风力和潮流同向时有

$\{\begin{array}{l}x=\left[\left(0.6\times 0.15+0.035\times 10\right)\times \cos \left(\frac{7\pi }{4}\right)\right]t+r\cos \alpha \\ y=\left[\left(0.6\times 0.15+0.035\times 10\right)\times \sin \left(\frac{7\pi }{4}\right)\right]t+r\sin \alpha \end{array}\left(0\le \alpha \le 2\pi \right)$. (20)

此时，取t = 60时，matelab建立模型得出在洋流和风力对油膜扩散规律分别如图10。

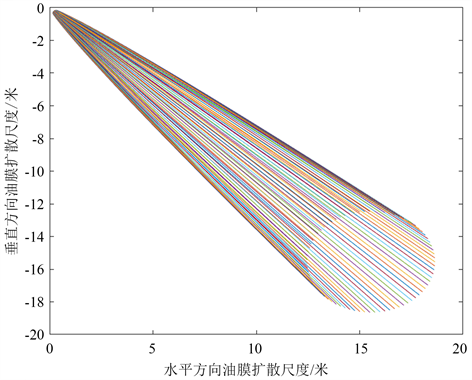
Figure 10. Diffusion of simultaneous ocean current and wind to oil film

图10. 同向洋流和风力对油膜扩散规律

当风力和潮流反向时有

$\{\begin{array}{l}x=\left[0.6\times 0.15\times \cos \left(\frac{\text{3}}{4}\pi \right)+0.035\times 10\times \cos \left(\frac{\text{7}}{4}\pi \right)\right]t+r\cos \alpha \\ y=\left[0.6\times 0.15\times \sin \left(\frac{\text{3}}{4}\pi \right)+0.035\times 10\times \sin \left(\frac{7\pi }{4}\right)\right]t+r\sin \alpha \end{array}\left(0\le \alpha \le 2\pi \right)$.(21)

当t = 60时，matelab建立模型得出在洋流和风力对油膜扩散规律分别如图11。

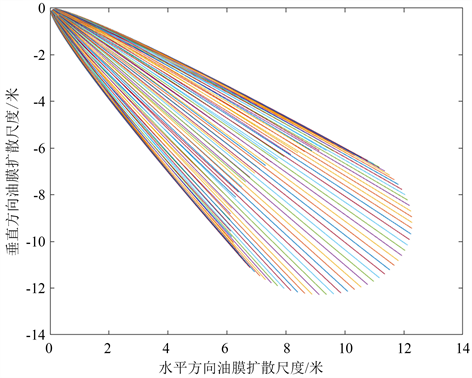
Figure 11. Reverse ocean current and wind force diffusion law against the oil film

图11. 反向洋流和风力对油膜扩散规律

在洋流和风力的影响下，油膜扩散方向受到水风和速度得影响最大，沿着水风和速度得方向扩散，面积呈水滴状分布。两种情况对比可知，当潮流改变时(风向和潮流反向)油膜整体方向移动方向没有太大改变，因此潮流对油膜移动影响远不及风力。模型与实际关于油膜扩散的的比较，如图12。

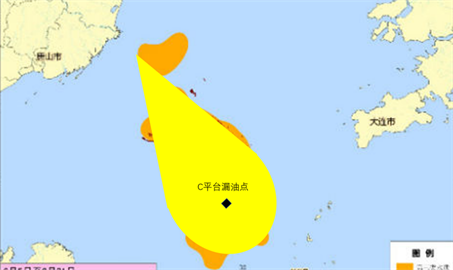
Figure 12. Comparison of the model with actual information on oil membrane diffusion

图12. 模型与实际关于油膜扩散的比较

浅黄色水滴形状为通过MATLAB建立的模型，橙色区域为实际油膜的扩散情况，可以直观的看到通过分析洋流和风力对油膜扩散所得出的数学模型与实际情况非常相近，进一步说明了建模的可行性。

3. 确定漏油点的方法

假设位于陆地上的蓬莱(蓬莱最北端)和大连(旅顺口) (旅顺口最南端)的监测点，分别在6月26日和6月27日检测到泄漏石油，假设只有一个泄漏点。

根据蓬莱、旅顺口和蓬莱19-3油田的具体位置抽象出点–线–面模型：

设旅顺口为点A，蓬莱为点B，泄露位置为点C(假设只有一个泄漏点)。

假设已知条件如下：1) 蓬莱(最北端)到旅顺口(最南端)的直线距离：AB。

2) 在蓬莱、旅顺口两个监测点的监测范围shi 以r为半径的圆面(假设两个监测点监测范围相同且是圆形)。

3) 溢油点的溢油速度

4) 蓬莱监测点监测到油膜的时间比旅顺口监测点监测到油膜的时间早一天。

5) 蓬莱监测点最开始监测到漏油时油膜边缘与监测边界的交点点D的方位，旅顺口监测点最开始监测到漏油时油膜边缘与监测边界的交点点E的方位。

下面分三种情况进行分析：

1) 在不考虑天气等因素时，即在平静的海面，海水各向同性，忽略原油挥发等因素，原油在海水中是以漏油点为中心扩散的，此时假设油膜扩散形状是以漏油点为圆心的圆，如图13。

圆B与圆C1相切于点D，过点D作两个圆的公切线 $l_1$，由切线的性质：圆心与切点的连线垂直于切线可知， $l_1\perp \text{CD}$， $l_1\perp \text{BD}$，故点B、D、C在同一条直线上。同理，圆A与圆C1相切于点E，过点E作两个圆的公切线 $l_2$，有 $l_2\perp \text{CE}$， $l_1\perp \text{AE}$，故点A、E、C在同一条直线上。

因此，由已知条件可以知道A、B、D、E点的位置，根据上述证明，连接点A，点E并延长线段AE，连接点B,点D并延长线段BD，直线AE与直线BD的交点就是漏油点点C的位置。又因为已知AE的长度为r，BD的长度为r，根据直线AE的倾斜角可以知道油膜在从C到E方向上的扩散速度V_CE，由于从C1扩散到C2的时间为一天，即86,400秒，从而可以得出CE的长度：86,400*V_CE，设圆C1的半径为x，利用三角形ΔABC中已知角度和边长，可以求解x的值，进而可以求得CE的长度，最终确定了点C的位置。

Figure 13. Monitoring diagram of oil leakage point (calm sea surface)

图13. 漏油点监测图(平静海面)

2) 在海洋中考虑溢油受到自身重力和某种外在因素影响的向下的扩散，此时油膜在x轴和y轴的扩散尺度受到影响而不同.

与1)的作法相同，连接点A，点E并延长线段AE，连接点B,点D并延长线段BD，通过实际作图，发现交点F与泄露位置C有较大偏差，而且油膜的各点的扩散速度不均匀会导致椭圆的形状各不相同，确定出来的点有多种情况。故而此种情况下无法确定泄漏石油的具体位置和区域，如图14所示。

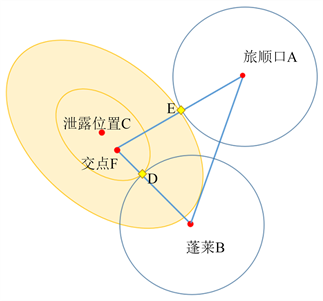
Figure 14. Monitoring diagram of oil leakage point (affected by gravity)

图14. 漏油点监测图(受重力影响)

3) 考虑洋流和风力对油膜扩散的影响

由于2)下的规则椭圆形扩散图形无法确认泄漏石油的具体位置和区域，更为复杂的情况三中考虑了实际情况中的多种因素，更加无法确定泄漏石油的具体位置和区域，如图15所示。

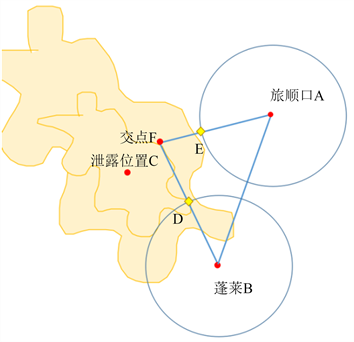
Figure 15. Monitoring diagram of oil leakage point (affected by ocean currents and wind speed)

图15. 漏油点监测图(受到洋流和风速影响)

因此，我们需要油膜边缘上更多点的位置得到油膜扩散的大致形状以便确定泄漏石油的具体位置和区域，故而需要在多个位置多个区域增设监测点。

4. 确定陆地监测站的最佳位置和最少数量

根据实际情况，泄漏点为平台C,考虑洋流和风力对油膜扩散的影响，此时油膜的扩散面积的数学模型为2.4.所述情况，该油膜形状的形成过程是由的椭圆形油膜向四周不规则的扩散而形成，可以将不规则的油膜理想为椭圆形，进而问题转化为如何确定一个椭圆。

由椭圆的一般方程为

$a{x}^2+b{y}^2+cx+dy+exy+f=0\left(a>0,b>0\right)$, (22)

看出确定一个椭圆需要确定 $a,b,c,d,e,f$ 六个未知数，两边同时除a得到

$x^2+g{y}^2+hx+iy+jxy+k=0\left(g>0\right)$,(23)

此时该方程只有 $g,h,i,j,k$ 五个未知数，所以只要找到五个点(至少三个不共面)就可以确定出椭圆的方程。

因此要确定该油膜泄漏点的位置，需要在渤海沿岸陆地至少建立五个监测站，下面分析五个监测站的最佳位置。

如图16在地图上给出渤海的地理位置以及沿岸的陆地，在图16中画出油膜扩散而形成的不规则椭圆，那么在油膜扩散过程中只需五个检测站的位置设在能最快检测出油膜扩散的边缘即可。

在已经设立的蓬莱和旅顺口的检测点的基础上增加监测点，首先考虑与旅顺口和蓬莱不共线陆地点设立第三个监测点，第三个检测点的位置选择在东营港，东营港、旅顺口和蓬莱构成三角区域，平台C的位置接近于该三角形的中心且该三角区域覆盖油膜扩散大部分面积，若发生泄漏事故已有的检测站配合东营港监测站的检测范围涵盖了大部分可能会扩散的范围，且会对油膜扩散面积有大致的了解。

第四个检测点的位置选择在北港，以上三个监测站能大概估计出油膜的扩散面积，分别位于蓬莱19-3油田的东南、东北、西南方位，而北港处在C平台的西北方位，考虑实际因素洋流和海风，洋流和海风的方向是季节性西北方向，如果在风速和洋流的合速度很大时，油膜向西北方向的扩散速度极快，北港检测站可以及时的检测出西北方向油膜的扩散情况，使得对扩散的油膜面积以及泄漏点有更准确，严谨的判断。增加西北方向上的北港检测点使得检测更加全方位，防御更加严谨。

第五个测点的位置选择在砣矶岛，该位置是与地图上C平台距离最近的陆地点，在无极端天气的情况下，若C平台发生泄漏该监测点可以第一时间检测到，为进一步核实和预警处理工作打下基础。

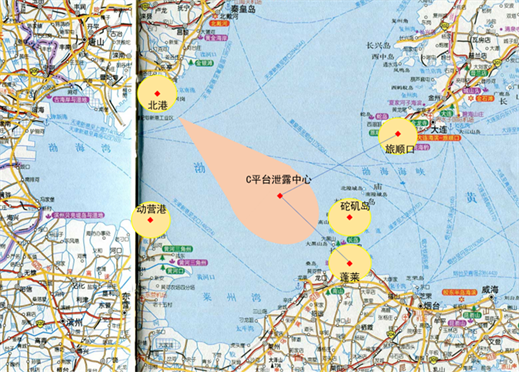
Figure 16. Location determination map of the best monitoring station

图16. 最佳监测站位置确定图

5. 总结

由上述问题的研究可知溢油的扩散与时间的关系以及变化规律，进一步可以得到如何最佳监测到泄漏点以及监测点最少的情况。本文给出了研究渤海湾蓬莱19-3油田漏油事故问题的系统方法，可以将此类已有扩散规律以及监测点判断问题推广到大多数海洋石油泄漏问题，便于工作人员及时监测到石油泄漏的发生，对海洋生态有持续发展具有积极意义。