1. 引言
汽车行驶工况(Driving Cycle)又称车辆测试循环,是通过数据分析所构建的描述汽车行驶的速度–时间曲线(见图1和图2)。它可以体现汽车道路行驶的运动学特征,模拟真实的交通状况,以测试车辆尾气排放和燃料消耗。此外,其在交通协同控制、新车评价、风险评估和车辆的设计、选型、匹配和控制策略等方面有着广泛的应用 [1]。目前,汽车发达国家都有自己的汽车行驶工况标准,而国外的行驶工况与国内行驶特征存在较大差异,直接采用则导致检测结果与实际数据往往存在较大误差。因此有必要建立反映国内行驶特点的典型行驶工况,提高检测结果的准确性和可靠性。
目前,构建行驶工况的常用方法有单纯的短行程法、基于聚类的方法和基于马尔可夫链的方法。短行程法将数据划分为短行程片段,通过分析片段的特征参数组合,生成相应的行驶工况。国外学者Lin等采用短片段划分以及随机过程选择方法构建了行驶工况 [2]。基于聚类的工况构建主要采用主成分分析法与聚类分析法相结合的研究方法,其中K-均值聚类分析法在构建城市汽车行驶工况中应用较多,通过
利用聚类算法对样本数据进行分类,根据分类结果从中筛选出最佳短行程样本,最后组合为典型工况。国外学者Fotouhi等采用K-Means聚类算法构建了德黑兰的行驶工况 [3]。同济大学胡志远利用短行程、主成分分析、聚类分析等方法对上海市公交车进行研究,生成了最优短行程组合 [4]。彭育辉等基于K-均值聚类方法对汽车行驶数据进行分析,提出一种以Silhouette函数筛选聚类结果,并根据聚类结果构建汽车行驶工况的方法 [5]。刘子谭等利用短行程法、主成分分析及聚类方法,并针对K-均值聚类稳定性较差的缺陷进行改进研究,将改进后的聚类方法应用于工况构建,生成了广州市行驶工况 [6]。
然而由于交通环境的影响,汽车实际行驶工况具有较大的随机性,也有文献对基于马尔可夫链的方法进行研究。姜平等利用聚类和马尔可夫方法构建了城市汽车行驶工况 [7]。苗强等采用聚类加马尔可夫链的方法构建了济南市公交车典型行驶工况 [8]。曹骞等利用主成分和聚类算法对大连市乘用车行驶数据进行统计分析,并基于马尔可夫链随机过程原理构建了行驶工况 [9]。李耀华等基于马尔可夫链构建了西安市城市公交线路工况 [1]。
基于上述分析,本文以给定的某城市轻型汽车实际道路行驶采集的近十九万条数据为基础,结合运动学片段、主成分分析以及聚类分析的主要方法来构建汽车行驶工况,将划分的运动学片段聚成3类,并结合相关系数法从各类片段库中选取最优片段,从而构建出能体现汽车行驶特征的典型汽车行驶工况。通过与采集的总样本数据进行对比分析,验证了所构建行驶工况的准确性。
2. 数据预处理
本文使用的数据集是某城市中给定的一辆轻型车辆采集的实际道路行驶数据,数据集中共有189,725条数据,如下表1所示。

Table 1. Vehicle driving data (partial)
表1. 汽车行驶数据(局部)
采集设备直接记录的原始采集数据通常会包括一些不良数据值,为了使得数据集中的汽车行驶数据更加合理有效,需要对原始数据进行处理与清洗。将不良数据分为缺失数据、尖点数据、毛刺数据以及怠速数据几个类型,数据处理主要包含以下四个方面:
1) 缺失数据插值处理。对于数据时间不连续的缺失数据,通过Matlab程序找出相邻两个时间间断,但是速度 > 0的节点进行插值处理。综合考虑各类因素,选择Hermite插值法。
2) 尖点数据的平滑处理。尖点数据是指两个相邻速度之间存在较大差异的数据,在行驶过程中,会因为各种原因造成异常加减速的数据。采用线性插值法对尖点数据选择进行平滑处理,令其等于前一个车速和后一个车速的平均数。
3) 毛刺数据删除处理。在车辆较长的怠速期间内,突然出现的个别汽车速度不为0的数据片段称作毛刺数据。而在汽车实际行驶状况中这种情况是不可能会出现的。而这种数据对后续的运动片段划分有较大的影响,因此需要清洗这些数据。
4) 怠速数据删除处理。汽车怠速是指当汽车停止运动但发动机保持最低转速时的状态。当怠速时间超过180 s时,一般视为异常情况。因此,需要将这种异常数据剔除掉。处理方法为:判断怠速的起点和终点,若连续怠速时间超过180 s,则保留靠近怠速终点的最后180秒数据,删除前面的异常数据。
使用Matlab软件进行数据处理,经处理后的数据集中的数据量如表2所示。

Table 2. Comparison of data volume before and after processing
表2. 处理前后数据量对比
3. 主成分分析与K-Means聚类分析
3.1. 运动学片段划分及特征参数提取
运动学片段也称为短行程,是指汽车从怠速状态开始到下一个怠速状态开始之间的速度范围,如图3所示,主要包括怠速阶段、加速阶段、匀速阶段和减速阶段 [10]。根据运动学片段来构建汽车行驶工况曲线,需要先对运动学片段进行划分和提取。将数据集中按时间排序的数据划分为多个运动学片段。通过编写对应的Python程序,划分出1421个运动学片段。
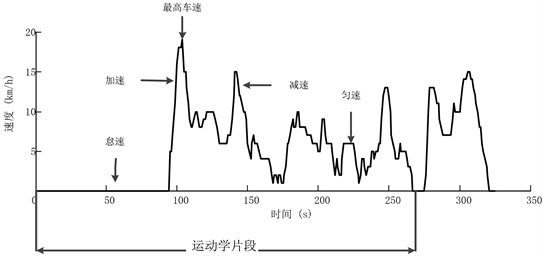
Figure 3. Definition of kinematic fragment
图3. 运动学片段的定义
汽车行驶工况是由多个具有代表性的运动学片段组合而成,选取具有代表性的运动学片段需要有计算出其特征参数作为标准与依据。在运动学片段的评估分析中,特征参数能够体现该运动学片段的交通特征。因此,对划分后的运动学片段进行特征参数提取和特征值计算。所选用的描述运动学片段的17个特征参数如下表3所示。

Table 3. Definition table of characteristic parameters
表3. 特征参数定义表
计算得到各个运动片段的每个运动特征参数值,部分数据如下表4所示。

Table 4. Characteristic values of each kinematic fragment (partial)
表4. 各运动学片段特征值(局部)
(a)
(b)
3.2. 主成分分析
原始数据常常存在量纲不一致的特点,首先采用最大最小标准化方法来进行数据标准化。其次,由于过大的数据量会大大降低计算效率,不利于聚类分析等各种问题,因此经过数据处理和运动学片段划分后,将利用主成分分析法对标准化处理之后的数据进行降维处理,目的是减少变量,提高后续计算能力。
运用Python软件进行主成分分析,贡献率从大到小依次排列并计算累计贡献率,输出结果见表5所示。通常选择累计贡献率小于85%的主成分,前4个主成分累计贡献率达88.59%,因此将用4个主成分替换17个特征参数用于工况的构建,将数据由17维降到了4维。

Table 5. Contribution rate and cumulative contribution rate of each principal component
表5. 各主成分贡献率及累计贡献率
3.3. K-Means聚类分析
主成分分析为聚类分析做准备,聚类分析是本文的重要方法,本文选择K-Means聚类方法对主成分评分数据进行处理。首先,采用手肘法来确定k值,也就是将数据分为几类。在K-Means算法中,k值的选择往往对聚类结果具有一定的影响,为了评估聚类效果,选用平方误差和(SSE)作为聚类结果的评估指标。通过每个簇点与其质心之间距离的平方来计算SSE [11]。手肘法可以用来反映k的不同取值和SSE的关系趋势,便于找到最佳k值。
对降维后的数据进行K-Means聚类分析,首先需要确定k值,手肘图如图4所示。根据手肘图的拐点,选择聚类簇个数k值为3,将所有的运动学片段分为3类,聚类效果图如图5所示。其中横纵坐标分别是降维后的数据的前两列。
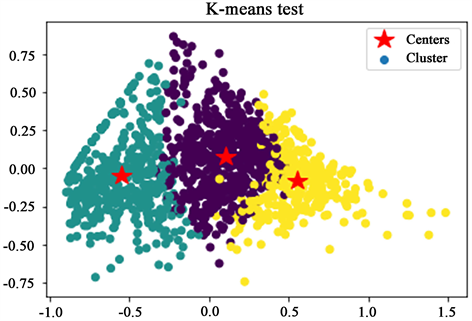
Figure 5. Clustering diagram of kinematic fragments
图5. 运动学片段聚类图
通过评估聚类中心的特征值,找到每一类数据的特点,聚类中心的特征值如表6所示。

Table 6. Eigenvalues of cluster centers
表6. 聚类中心的特征值
从以上的特征值表中,发现第三类运动学片段中怠速比例最高,达到69.9%,说明第三类片段代表的是堵车严重的路段,而第一二类数据的怠速时间比相对于第三类则明显减少,并且第二类数据的平均速度是三类数据中最高的,是道路通畅的路段。
4. 行驶工况构建与验证
4.1. 行驶工况构建
原始数据经过清洗、运动学片段的划分、降维与分类后,考虑到每个分类中的数据量还会较大,因此需要从每类运动学片段中抽取合适的片段来合成行驶工况。在选取运动学片段时考虑它们的相关性,即相关系数。在每个聚类中选取与该类特征值相关系数最大的若干代表性运动学片段构建车辆的行驶工况。计算出各类运动学片段和它所在的类别中心的相关系数,列取出相关系数较大的前10个运动片段如表7所示。

Table 7. Correlation coefficients of various kinematic fragments
表7. 各类运动学片段相关系数大小
由于拟定构建的行驶工况的时间长度为1200~1300 s,分别从第一类工况中选取3个运动学片段,从第二类工况中选取4个运动学片段,从第三类工况中选取2个运动学片段。将所选运动学片段首尾相连,最终构建的长度为1265 s的行驶工况如图6所示,横坐标为时间(s),纵坐标为速度(km/h)。
4.2. 行驶工况验证
由于前期行驶工况的构建是由对于试验数据采取统计的方法得到的,所以要验证其与原始数据之间的差异 [11]。选取能反映总体统计情况的特征参数作为分析指标,计算所构建道路行驶工况及相应的总体行驶工况的相对误差和绝对误差,并根据计算结果分析所建道路行驶工况的有效性。所选取的指标特征参数如下表8所示。
是构建出道路行驶工况的特征参数,
是工况所对应总体的特征参数。相对误差
,绝对误差
。

Table 8. Parameters used in error analysis
表8. 误差分析所用参数
根据相对误差和绝对误差的公式,总体数据与构建的汽车行驶工况的误差分析如表9所示。从表中可知,所构建的行驶工况的特征参数中,多数参数小于10%,尤其平均加速度的相对误差为0.75%,从特征参数的验证结果来看,行驶工况的构建方案是比较合理的。

Table 9. Error analysis of vehicle driving cycle
表9. 汽车行驶工况的误差分析
5. 总结与展望
本文以某城市轻型汽车实际道路行驶采集的近十九万条数据作为实验数据集,划分出1421个运动学片段,提取描述运动学片段的17个特征参数,采用主成分分析和K-Means聚类算法对特征参数矩阵进行降维和分类处理,将运动学片段分为3类,并结合相关系数法从3类运动学片段库中选取代表性片段,从而构建出了符合数据源中汽车行驶特征,时长1265 s的车辆行驶工况。通过分析实验数据与行驶工况的特征参数,验证了工况的准确性。
实验结果表明,本文中行驶工况的构建方案比较合理,拟合出的轻型汽车行驶工况能反映真实数据特征,符合城市道路实际工况。然而本文对于工况构建的指标没有考虑到现实生活中存在的地形、环境、温度等不确定性因素,这些因素均可能影响运动学片段的走势,未来可以进一步结合马尔科夫链方法进行研究。