基于Lasso回归和神经网络的辛烷值损失预测模型

Octane Value Loss Prediction Model Based on Lasso Regression and Neural Network

摘要: 由于目前的炼油工艺过程具有复杂性和设备多样性，它们的操作变量间不仅仅是简单的线性关系，而是具有高度非线性和相互强耦联的关系，而且现阶段的研究中传统数据关联模型的操作变量较少，对过程损失预测的响应不及时，所以效果并不理想。本文根据催化裂化汽油精制装置采集的325个样本数据，通过lasso回归结合spearman相关系数筛选出影响辛烷值缺失的主要操作变量，通过BP神经网络建立了辛烷值损失的预测模型，并验证了预测模型的有效性。

Abstract: Due to the complexity of the current refining process and the diversity of equipment, their operating variables are not only a simple linear relationship, but have a highly nonlinear and strongly coupled relationship, and the variables in the traditional data correlation model are relatively Less; the mechanism modeling requires higher analysis of raw materials, and the response to process loss prediction is not timely, so the effect is not ideal. In this paper, based on 325 sample data collected by catalytic cracking gasoline refining unit, the main operating variables that affect the missing octane value are screened out by lasso regression combined with Spearman correlation coefficient, and the prediction model of octane value loss is established by BP neural network, and the prediction model validity is verified.

1. 引言

汽油是小型车辆主要的燃料之一，汽油的燃烧会产生大量的尾气，尾气中含有的有害物质对大气环境有重要影响。因此，从环境可持续发展的角度，世界各国都制定了日益严格的汽油质量标准。汽油清洁化的重点是降低汽油中硫和烯烃含量的同时尽量避免其辛烷值的损失。即使在当代国内最先进的技术基础上，对催化裂化汽油进行脱硫和降烯烃，也会使汽油的辛烷值大幅缺失，因此预测辛烷值的损失是进行脱硫和降烯烃的重要前提。

化工过程的建模一般是通过数据关联或机理建模的方法来实现的，取得了一定的成果。但是由于炼油工艺过程的复杂性以及设备的多样性，它们的操作变量(控制变量)之间具有高度非线性和相互强耦联的关系，而且传统的数据关联模型 [1] [2] [3] 中变量相对较少、机理建模对原料的分析要求较高，对过程损失预测的响应不及时，所以效果并不理想。在此基础上，本文利用Lasso回归和BP神经网络模型可以有效预测化工过程中汽油辛烷值损失。

2. 数据预处理

2.1. 数据问题描述

本文是以某石化企业原始数据为例，数据采集操作位点共354个，样本量为325个。在原始数据中，大部分变量数据正常，但每套装置的数据均有部分位点存在问题：有些变量只含有部分时间段的数据，有些变量的数据全部或部分为空值。针对此类问题，采用Matlab软件编写含有贝塞尔公式的程序，根据3σ准则去除异常值，然后对于部分数据为空值的位点，空值处用其他数据的平均值代替。将样本以辛烷值数据测定的时间点为基准时间，取其前2个小时的操作变量数据的平均值作为对应辛烷值的操作变量数据。

2.2. 预处理过程

对于原始数据的处理流程如图1所示。

现实中缺失值的产生多种多样，对于不同缺失值的产生原因，其处理方法会对数据的可靠性产生较大的影响，所给的原始数据是由于每套装置的数据均有部分位点存在问题所引起的缺失值，属于完全随机缺失，数据的缺失是随机的，它的缺失不依赖于任何操作变量。简单删除法是对缺失值进行处理的最原始方法。它将存在缺失值的个案删除。如果数据缺失问题可以通过简单的删除小部分样本来达到目标，那么这个方法是最有效的。

Figure 1. Data processing flow chart

图1. 数据处理流程图

将原始数据进行无效样本处理，对数据的每个字段的缺失值进行统计，设定一个合理的阈值，如果字段缺失比例高于阈值，对字段进行删除处理。删除样本数据中全部为空值的位点，对于有些空值的位点，空值处使用所存在数据的平均值代替。对于异常值根据拉依达准则(3σ准则)进行去除。

3σ准则：设对被测量变量进行等精度测量，得到 $x_1,x_2,\cdots ,x_n$，算出其算术平均值x及剩余误差 $v_i=x_i-x\left(i=1,2,\cdots ,n\right)$，并按贝塞尔公式算出标准误差σ，若某个测量值x_b的剩余误差v_b ( $1\le b\le n$ )，满足 $\left|v_b\right|=\left|x_b-x\right|>3\sigma$，则认为x_b是含有粗大误差值的坏值，应予剔除。贝塞尔公式 [4] 如下：

$\sigma ={\left[\frac{1}{n-1}{\displaystyle {\sum }_{}^n{v}_i^2}\right]}^{1/2}={\left\{\left[{\displaystyle {\sum }_{i=1}^n{x}_i^2-{\left({\displaystyle {\sum }_{i=1}^n{x}_i}\right)}^2}/n\right]/\left(n-1\right)\right\}}^{1/2}$ (1)

2.3. 预处理结果

通过对原始数据进行空值处理、数据阈值处理，将数据修正、剔除、替代等处理，得到更能反应操作变量对辛烷值损失变化的样本数据，其中数据畸变严重的285和313号样本，处理后的部分结果如表1所示。

Table 1. Some operating variables of processed samples

表1. 处理后样本的部分操作变量

3. 主要变量提取

工程技术应用中经常使用先降维后建模的方法，这有利于忽略次要因素，发现并分析影响模型的主要变量与因素，通过对变量的分析，我们选择Lasso回归 [5] 和斯皮尔曼Spearman相关系数两种方法筛选建模的主要变量。考虑到硫含量不低于5 μg/g，辛烷值RON属于产品性质，所以降维时不考虑硫含量和辛烷值RON。因此我们将辛烷值RON损失作为因变量，其余365个变量作为自变量进行降维，降维主要步骤如图2所示。

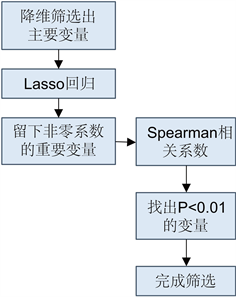
Figure 2. Main steps of dimensionality reduction

图2. 降维主要步骤图

3.1. Lasso回归方法

Lasso回归主要使用K折交叉验证的方法来获得最佳的调整参数。K折交叉验证的实质是将样本数据随机划分为K个等分。把第1个子样本作为“验证集”先不使用此样本，使用其余的K − 1个子样本为“训练集”来估算这个模型，再以此为基础去预测之前的第1个子样本，并计算第1个子样本的“均方预测误差”。

接着，将第2个子样本作为验证集，先不用此样本，去使用其余的K − 1个子样本，作为训练集来预测第2个子样本，并计算第2个子样本的MSPE。依次类推，将所有子样本的均方预测误差加总，之后可以求出整体样本的MSPE。最后，通过调整参数，可以获得整个样本的最小MSPE。

3.2. Lasso回归的操作过程

在Lasso回归前，先将数据标准化预处理，这里使用Matlab的zscore函数标准化处理。将标准化后的数据用Stata软件进行Lasso回归，Lasso回归的主要代码如下：

Cvlasso Y $X_1,X_2,X_3,\cdots ,X_n$ lopt seed (520)

代码中的“lopt”表示选择使MSPE最小的 $\lambda$，“seed (520)”表示随机数种子数，此处我们将随机种子数设为520，随机种子数可随机设定，这样的结果可具有重复性。默认K = 10，K表示10折交叉验证。其中Y表示因变量 $X_1,X_2,X_3,\cdots ,X_n$ 表示自变量。

对因变量RON损失和365个自变量使用lasso回归，观察lasso回归结果表中回归系数不为0的变量，这些变量是我们最终需要留下来的重要变量，其余未出现在表中的变量被视为不重要变量，不重要变量将被剔除，主要步骤的流程图如图3所示。

Lasso回归的主要优点在于，它可以充分稳定的筛选出变量、建立具有概化能力和预测能力的模型。此外Lasso回归还可以处理多维度问题和多重共线性问题，处理后的结果如表2所示。

从表2中可知，Lasso回归后，共留下的18个重要变量，但为了更好的筛选出重要变量，接下来进行斯皮尔曼Spearman相关系数分析。

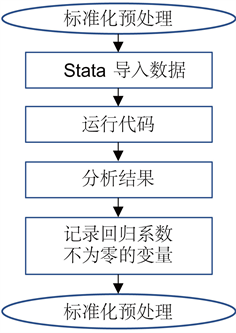
Figure 3. Lasso main steps flow chart

图3. Lasso主要步骤流程图

Table 2. Lasso regression results

表2. Lasso回归结果表

4. 显著性分析

4.1. 斯皮尔曼Spearman显著性原理

假设有两组向量分别为X和Y，其秩序分别为 $R\left(X\right)$ 和 $R\left(Y\right)$，这里 $R\left(X_i\right)=K$ 表示为X_i是序列X中的第K大(或者第K小)，则 $\text{SROCC}=\left(X,Y\right)=\text{PLCC}\left(R\left(X\right),R\left(Y\right)\right)$，其中PLCC是Pearson线性相关系数。SROCC被认为是最好的非线性相关指标，公式中的SROCC只与序列元素中的排序有关。所以尽管X或Y被任何单调非线性变换影响作用(比如对数变换、指数变换等等)，这些因素都不会对SROCC造成任何的改变，是因为它们不会影响元素的排序。同时可以认为秩相关系数是单调性相关，也就是说只要X和Y具有单调的函数关系，那么X和Y就是完全斯皮尔曼相关的，这与Pearson相关系数的相关性不同，Pearson只有变量之间是线性关系时才是完全相关的，此外，斯皮尔曼不需要先验知识，知道其参数便可以准确获取X和Y的采样概率分布。

一种确定被观测数据的 $\rho$ 值的方法 [6]，看它是否显著不为零(r总是有 $1\ge r\ge -1$ )，计算它是否有大于r的概率，依次作为原假设，并使用分层排列测试进行检验。这种方法的优点在于，它考虑了样本中的数据个数和在使用的样本的等级相关系数的风险。

另外的一种方法是使用皮尔逊积矩中使用到的费雪交换。也就是， $\rho$ 的置信区间和零检验可以通过费雪变换获得

$F\left(r\right)=\frac{1}{2}\ln \frac{1+r}{1-r}=\text{arctanh}\left(r\right)$ (2)

如果F(r)是r的Fisher变换，则

$z=\sqrt{\frac{n-3}{1.06}}F\left(r\right)$ (3)

是r的 $z^{-}$ 值，其中，r在统计依赖 $\left(\rho =0\right)$ 的零假设下近似服从标准正态分布。

显著性为

$t=\sqrt{\frac{n-2}{1-r^2}}$ (4)

其在零假设下近似服从自由度为 $n-\text{2}$ 的t分布。

一般地，斯皮尔曼相关系数在有三个或更多条件的情况下是有用的。并且，它预测观测数据有一个特定的顺序。

4.2. 斯皮尔曼Spearman显著性计算

这里使用了两种方法计算斯皮尔曼相关系数。

1) 用Matlab计算斯皮尔曼相关系数，Matlab主要代码如下。

[R, P] = corr (Test, ‘type’, ‘Spearman’)

其中Test是输入的参数，我们取Lasso回归筛选留下的变量(见表2)和RON损失变量进行斯皮尔曼相关系数的假设检验。

2) 使用Spss软件计算斯皮尔曼相关系数，主要步骤流程图如图4所示。

输出的斯皮尔曼相关系数表我们只取第一行，代表每个自变量与因变量RON损失的相关性，如表3所示。

通过对表2中分析，我们挑选出^**的变量，这些变量在P < 0.01时相关性显著。筛选出的变量如图4所示。

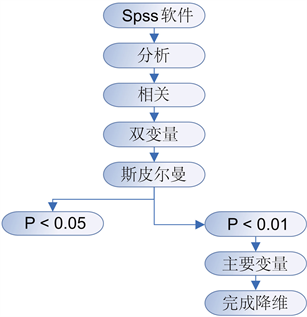
Figure 4. Step diagram of calculating Spearman correlation coefficient

图4. 计算斯皮尔曼相关系数的步骤图

Table 3. Spearman correlation coefficient table

表3. 斯皮尔曼相关系数表

其中^**表示在0.01级别(双尾)关性显著，^*表示在0.01级别(双尾)相关性显著。

经过Lasso回归和斯皮尔曼相关系数的两轮筛选，最终得到13个主要变量，如表4所示。

Table 4. Main variables of modeling

表4. 建模主要变量表

5. 建立辛烷值(RON)损失预测模型

5.1. BP神经网络模型

Back Propagation神经网络，简称为BP神经网络 [7]，是一个误差反传误差反向传播算法的学习过程，其具体过程包括信息正向传播，误差进行反向回传。里面囊括了作用函数模型、自学习模型、输入输出模型和误差计算模型。这些模块中，自学习模型可以对事物的发展状况建立模型，从而实现预测的功能。

一般实际应用中，BP神经网络被广泛应用，80%~90%的人工神经网络模型是采用BP网络或它的变化形式，它是前馈网络的核心部分，体现了人工神经网络最精华的部分。由于这些突出的优点，结合四个指标之间存在的非线性问题，本文认为BP神经网络在分析筛选后的操作变量和辛烷值减少之间的关系中的应用是可行的。BP神经网络用含有隐含层的三层结构网络类型，示意图如图5所示。

Figure 5. Structural network with one hidden layer

图5. 含有一个隐含层的结构网络

5.2. 模型的建立

具体框架图如图6所示。

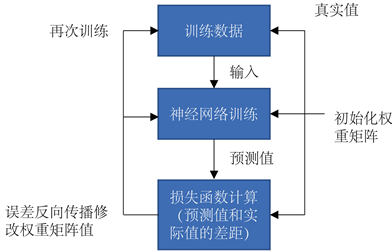
Figure 6. BP neural network framework

图6. BP神经网络框架图

由框架图我们可直观的看出神经网络模型的建立，离不开多次的求解和迭代，也正是这种迭代过程，BP神经元的过拟合问题 [8] 一直是建立模型中不可忽视的一部分，因此为了减少过拟合现象，我们首先将325个样本拆成300个训练集以及25个验证集，如表5~7所示。

Table 5. Target table of 300 training sets

表5. 300个训练集目标表

Table 6. 25 validation set input tables

表6. 25个验证集输入表

Table 7. 300 training set input tables

表7. 300个训练集输入表

其次在建模的过程中由于各种操作指标的单位不一，数量级的差别又大，为了消除这些因素在训练过程中产生的影响，本文我们对数据进行了无量纲化处理 [9] 即对数据进行归一化，对300个训练集的自变量采用以下公式进行先行转换。

$X_k=\left(X_K-X_{\min }\right)/\left(X_{\max }-X_{\min }\right)$ (5)

其中， $X_{\min }$ 是数据中的最小数， $X_{\max }$ 是数据中的最大数。

最后，为了确定最优的模型以及减小过拟合的影响，我们通过控制变量法取不同的神经元，不同的训练算法来得出一个最佳的神经网络模型，训练方法如下：

1) 量化共轭梯度法

量化共轭梯度法是梯度法中的一种改进的方法，它可以很好地填补梯度法带来的振荡以及收敛性不好的缺陷。基本思想是通过寻找与负梯度方向和上一次搜索反向的共轭方向作为新的方向迭代。

我们选择量化共轭梯度法作为训练方法，选取了不同神经元进行模拟，模拟结果如图7所示。

Figure 7. Mean square error diagram with neurons of 20

图7. 神经元为20的均方误差图

Figure 8. R² Diagram with neuron of 20

图8. 神经元为20的R²图

由图8可知：在神经元个数为20时，进行了28次迭代并且在第22次迭代时均方误差达到最小值为0.053698，但是总的拟合优度都在50%左右，优化的结果较差。

2) 莱文贝格–马夸特法

此算法可理解为借助执行时修改参数达到结合高斯–牛顿算法以及梯度下降法的优点，并对两者之不足做一些改善，比如高斯–牛顿算法的反矩阵不存在或者说初始值离局部极小值太远，而且能提供非线性最小化的数值解答。

在这里我们选择莱文贝格–马夸特法作为训练方法，选取不同神经元进行模拟，模拟结果如图9所示。

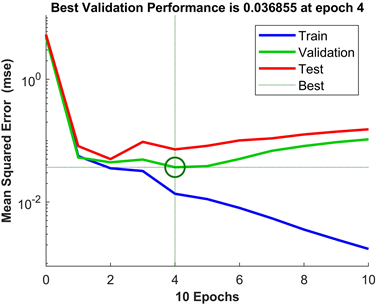
Figure 9. Mean square error diagram with neurons of 20

图9. 神经元为20的均方误差图

Figure 10. R² Diagram with neuron of 20

图10. 神经元为20的R²图

由图10可知：在神经元个数为20时，进行了10次迭代并且在第4次迭代时均方误差达到最小值为0.036855，但是总的拟合优度达到74%，优化的结果较好。

综上所述：选取神经元为20的莱文贝格–马夸特法作为我们的神经网络预测模型，它的迭代速度最快，总的拟合优度也是最好的。

我们把剩余的25组验证集数据导入到上文所得的最优神经网络预测模型中，并且用Matlab损失函数计算出的辛烷损失值与真实值进行了比较，比较结果图如图11所示。

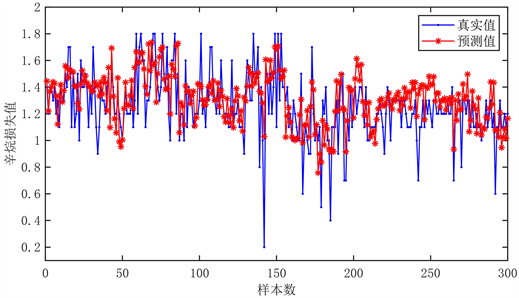
Figure 11. Prediction diagram of octane loss value in training set

图11. 训练集辛烷损失值预测图

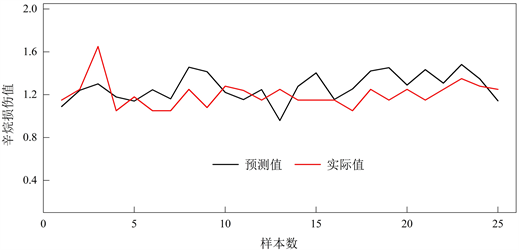
Figure 12. Prediction diagram of octane damage value of validation set

图12. 验证集辛烷损伤值预测图

从图12我们可以明显的看出，预测值与实际值相差很小，并且无论是训练集还是预测集所得到的辛烷损伤预测图的变化趋势基本相同，这从另一个方面间接证明了我们选用的预测模型不仅减小了神经网络预测法常有的过拟合曲线，而且在变量的正确选取以及预测效果上都是显著的。

6. 结束语

通过Lasso回归和神经网络的对汽油辛烷值的预测分析，可以得到以下结论：

1) 通过Lasso回归和斯皮尔曼Spearman相关系数两种方法筛选建模的主要变量，分别是精制汽油出装置温度、燃料气进装置流量、0.3 MPa凝结水出装置流量、除氧水进装置流量、D203出口燃料气流量、D-106热氮气流量、D-102温度、原料汽油硫含量、稳定塔顶回流流量、P-101B入口过滤器差压、F-101辐射室出口压力、S_ZORBAT-0001以及E-101壳程入口总管温度13个主要变量，对汽油辛烷值的含量大小起到主导作用。

2) 在基于BP神经网络模型得到的最优损失预测模型中，通过数据挖掘的方法可以有效地预测主要参数变化的情况下汽油辛烷值的损失。