强夯设计参数对高填方粉土路堤加固效果研究

Study on Improvement Effect of Dynamic Compaction Design Parameters on High Fill Silt Road Embankment

摘要: 建立高填方粉土路堤强夯ABAQUS有限元分析模型，并以山东地区某高速公路高填方粉土路堤强夯加固试验路为依托对该模型进行验证，研究强夯施工设计参数对高填方粉土路堤加固效果的影响。以路堤底部达到90%压实度为有效加固指标，采用1500 kN∙m夯击能、夯点间距3.2 m、夯击10次的设计参数可对4 m高粉土路堤进行有效加固；同时优选7000 kN∙m夯击能开展8 m高粉土路堤强夯加固试验，以达到90%压实度的加固区域作为路堤强夯的有效加固范围，该高度松填粉土路堤的建议强夯设计参数为：夯击能7000 kN∙m、夯间距5.2 m、夯击次数14次。

Abstract: The ABAQUS finite element analysis model of dynamic compaction was established, and the model was verified based on the dynamic compaction reinforcement test road of an expressway in Shandong province, and the influence of construction design parameters of dynamic compaction on the reinforcement effect of high-fill silt road embankment was studied. With 90% compaction at the bottom of embankment as the effective reinforcement index, 4 m high silt soil embankment can be effectively strengthened by using the tamping energy of 1500 kN∙m, the distance between tamping points of 3.2 m and 10 times of tamping. At the same time, the compaction capacity of 7000 kN∙m is selected to carry out the dynamic compaction reinforcement test of 8 m high silt soil embankment, and the reinforcement area with 90% compaction degree is taken as the effective consolidation range of embankment dynamic compaction. The recommended dynamic compaction design parameters of this highly loose filled silt soil embankment are: compaction energy is 7000 kN∙m, compaction interval is 5.2 m, and 14 times compaction.

1. 引言

黄泛区主要由黄河泛滥冲积而成，包括我国河南、山东、河北、安徽、江苏等的大片区域，是我国地质、水文条件极具特色的一个区域，该区域土质以粉土为主 [1] [2]，该类土粉粒含量极高，黏粒含量低，级配差，磨圆度高，因而结构松散、强度低，传统分层压实方法不仅施工效率低、而且压实困难。在当前的黄泛区高速公路施工中，传统的施工方法具有较大的局限性。

强夯技术是一种将大吨位夯锤提起到一定高度后自由下落，以达到加固土体地基的目的，通过调整强夯夯击能的大小，可以实现地基3~10 m深度的有效加固，被广泛应用于各类地基加固 [3] [4]。由于强夯加固具有技术成熟、施工简便、经济效益高、加固厚度大、施工速度快等优点，其工程应用日益普遍 [5]。在道路工程中，强夯也常用于老路堤的加固处理甚至新路堤的快速填筑，目前已有工程对黄泛区粉土路堤进行强夯处理 [6]，并取得良好的加固效果。然而，强夯法在路堤填筑的应用中 [7] 仍存在一些问题。在工程中，强夯法的施工参数一般根据试夯结果确定 [8]，试夯过程繁琐且耗费较高的成本，如何更高效地确定这些设计参数仍有待研究；利用强夯法填筑粉土路基时，路基的压实度在水平和深度方向具有不均匀性，影响路堤的填筑质量，进而影响道路的使用性能，因此还应对夯后路堤的加固效果进行探讨和分析 [9]。

基于以上问题，本文依托山东地区某高速公路建设工程，并与室内有限元模型模拟试验结果进行对照，分别开展了4 m、8 m两种填高粉土路堤的强夯加固研究，获得了高填方粉土路堤的强夯加固规律，并提出相应的强夯设计参数，可为后续的强夯加固设计参数确定提供参考。

2. 强夯模型

2.1. 材料本构模型

由于帽盖塑性模型可以有效地考虑由于压实和剪切破坏引起的土体硬化，因此许多研究者已经成功地将帽盖塑性模型应用于强夯模拟 [10] [11]。帽盖塑性模型有两个屈服面：第一个是表征剪切破坏的Drucker-Prager模型固定屈服面；第二个是在塑性体积应变变化过程定义硬化的移动帽盖面。p-q (p为主应力、q为偏应力)坐标体系下的帽盖模型如图1所示 [12]。

Figure 1. p-q cap model in coordinate system

图1. p-q坐标体系下的帽盖模型

考虑强夯大变形问题，以及为了通过子程序实现强夯加固区土体力学参数随夯击次数的变化，路堤土体本构模型选用Cap Plasticity模型；地基土体不考虑强夯过程中土体参数的变化 [13]，选用Mohr-Coulomb模型。考虑夯锤相对粉土路堤的材料属性，可将之视为刚体。强夯过程中土体力学参数会发生变化，本论文在数值模拟过程中，依据下列公式编写二次开发程序，可分别实现土体模量、密度随强夯过程的动态变化及土体粘聚力d、摩擦角β随压实度的动态变化。

$K=k_r{P}_a{\left(\frac{P^{\prime }}{P_a}\right)}^{0.5}$ (1)

$k_r=\eta \exp \left(\gamma D_r\right)$ (2)

${\gamma }_{soil}=\frac{G_s{\gamma }_w}{1+e}$ (3)

式中： $k_r$ ——模量系数(Pa)；

$D_r$ ——相对密度；

${\gamma }_{soil}$ ——土体重度；

$P_a$ ——大气压(Pa)；

$G_s$ ——土的比重；

$P^{\prime }$ ——平均等效压力(Pa)；

${\gamma }_w$ ——水的重度；

$K$ ——体积模量(Pa)；

$\eta ,\lambda$ ——土壤常数；

$e$ ——土体孔隙。

根据室内直剪试验对摩尔库伦模型的压实度k与粘聚力c、摩擦角φ的对应关系进行拟合，得到压实度k与粘聚力c、摩擦角φ的函数关系分别为：

$c=0.0168k^3-4.68k^2+436.258k-13499.014\left(R^2=0.993\right)$ (4)

$\phi =0.0176k^2-2.794k+139.654\left(R^2=0.984\right)$ (5)

摩尔库伦模型粘聚力c、摩擦角φ与帽盖模型粘聚力d、摩擦角β的对应关系为：

$\tan \beta =\frac{6\sin \phi }{3-\sin \phi }$ (6)

$d=\frac{18c\cos \phi }{3-\sin \phi }$ (7)

式中：k——压实度；

c——摩尔库伦模型粘聚力(kPa)；

φ——摩尔库伦模型摩擦角(˚)；

d——帽盖塑性模型粘聚力(kPa)；

β——帽盖塑性模型摩擦角(˚)。

根据公式(4)~(7)，即可得出帽盖塑性模型压实度k与帽盖模型粘聚力d、摩擦角β的对应关系，为后续的数值模拟提供参考依据。

路基填料、地基土体和夯锤参数如表1所示。采用瑞利阻尼表征强夯过程对应大应变下的路基填料阻尼，阻尼系数分别设置为α = 6.573，β = 0.000255。

Table 1. Physical and mechanical indexes of materials

表1. 材料物理力学指标

2.2. 强夯有限元模型

几何模型包括两部分：土体(part 1，包括地基、粉土路堤)和夯锤(part 2)。为节省计算时间，地基和路堤仅取1/2建模。根据相关研究 [14]，保证计算精度的网格尺寸应满足 $\Delta l\le \left(\frac{1}{8}~\frac{1}{10}\right)\lambda$，强夯振动的波

长λ约为4 m，因此网格尺寸 $\Delta l\le \left(0.4~0.5\right)\text{m}$。为了保证计算结果的准确性同时缩短计算时间，距离夯点较近处网格划分较密，设置为0.2 m，距离夯点较远处网格划分较疏，设置为0.5 m。

夯锤对路堤的冲击荷载可简化为三角形的形式，如图2所示。接触时间t_N、最大冲击应力P_max通过下面的公式 [15] 估算得到。

$P_{\max }=\frac{v_0\sqrt{mS}}{\text{π}{r}^2}$ (8)

$t_N=\text{π}\sqrt{\frac{m}{S}}$ (9)

式中：v₀——夯锤到达地表的速度(m/s)；

m——夯锤质量(kg)；

r——夯锤半径(m)；

S——弹性常数，记作 $S=\frac{2rE}{1-V^2}$，E和v分别为路堤的变形模量和泊松比。

Figure 2. Diagram of impact load

图2. 冲击荷载示意图

3. 高填方路堤强夯加固

3.1. 4 m高路堤强夯加固

结合黄泛平原区某高速公路现场试验，开展4 m高度松铺路堤的强夯现场试验和室内有限元模拟，强夯夯击能采用1500 kN∙m，路堤填土为粉质土。强夯工艺参数见表2，采用隔点隔行跳夯方式进行点夯。

Table 2. Technical parameters of dynamic compaction of 4 m high silt embankment

表2. 4 m高度粉土路堤强夯工艺参数

建立三维强夯有限元模型，其中地基尺寸：26 m × 15 m × 16 m；路堤顶面尺寸：15 m × 15 m、路堤高度：4 m、边坡坡度1:1.5；坡脚距离地基边界5 m；夯点间距：3.2 m。每次夯击过程的计算时间取0.4秒。将夯击能换算为三角形荷载如图3所示。模型及网格划分如图4所示，共A、B、C、D4个夯击点位，夯击次序为A→B→C→D，每个夯点连续夯击10次。

Figure 3. 1500 kN∙m level impact load

图3. 1500 kN∙m能级冲击荷载

Figure 4. Finite element model and meshing

图4. 有限元模型及网格化分

夯沉量的数值模拟与现场试夯结果对比如图5。为保证试验可靠性，确定止夯击数为10；单击夯沉量、累计总夯沉量数据表明，数值模拟与现场试夯结果具有较高的吻合度，单击夯沉量误差小于3 cm，累计夯沉量误差小于1 cm，表明基于帽盖模型二次开发的强夯数值模拟方法可靠。

Figure 5. Comparison chart of ramming weight

图5. 夯沉量对比图

定义夯点A为测点1，夯点A、D中间为测点2，夯点A、B中间为测点3。提取模型测点1、2、3正下方不同深度的密度结果，换算为压实度。采用开挖探坑的方法，检测试验路对应位置的压实度，与数值模拟夯击结果进行对比如图6。

由图6可以看出，除夯锤下方1.5 m范围内数值模拟结果偏高外，其它深度的数值模拟结果和现场实测结果基本吻合，两者差别在1%以内。因此，对于4 m高度松铺路堤，采用1500 kN∙m的夯击能可以将路基全深度范围内的压实度提高至90%以上。

Figure 6. Compactness comparison diagram of each measuring point

图6. 各测点压实度对比图

根据4 m高路堤强夯加固效果可以看出，根据现场工况构建的有限元模型模拟结果与现场试验结果基本吻合，两者实验结果都证明：对于用1500 kN∙m的夯击能4 m高度松铺路堤的加固效果十分明显，可将路基全深度范围内的压实度提高到90%以上。

3.2. 8 m高路堤强夯加固

1) 单点夯分析

针对8 m高的路基填筑高度，依据《建筑地基处理技术规范》 (JGJ 79-2012) [16]，初步选取6000 kN∙m、6500 kN∙m、7000 kN∙m、7500 kN∙m四种单击夯击能，进行单点夯数值模拟试验，选取最佳单击夯击能。路堤高度为8 m、夯锤尺寸为2.5 m × 1 m (直径 × 高度)，模型及网格划分如图7所示。分别计算不同夯击能夯锤底部的接触应力、作用时间，汇总计算结果如表3所示。

Figure 7. Finite element model and meshing

图7. 有限元模型及网格化分

Table 3. Summary table of impact load parameters of different ramming energy

表3. 不同夯击能冲击荷载参数汇总表

8 m高路堤在不同夯击能作用下夯沉量与夯击次数的关系如图8所示。可以看出，在6000 kN∙m、6500 kN∙m、7000 kN∙m和7500 kN∙m能级的强夯作用下，第1击的夯沉量分别为47.7 cm、50.0 cm、52.2 cm、54.2 cm，约占各能级强夯作用下最终夯沉量的20%，此后每一击的夯沉量逐渐减小，并趋于收敛。6000 kN∙m、6500 kN∙m、7000 kN∙m、7500 kN∙m能级的强夯作用下，15击夯沉量分别为238.0 cm、253.2 cm、268.5 cm、280.0 cm。7500 kN∙m与6000 kN∙m的夯击能相比相比，夯沉量增大了17.65%，说明当夯击次数相同时，单击夯击能越高，对路堤的压实效果越好。

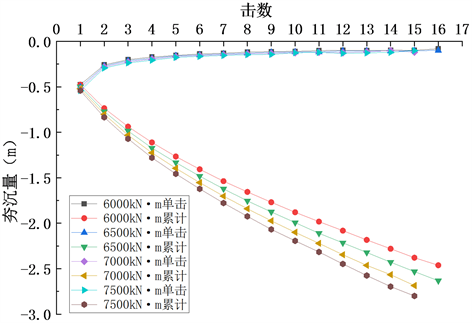
Figure 8. The relation curve of ramming times and ramming weight of different ramming energy

图8. 不同夯击能夯击次数–夯沉量关系曲线

探究路堤底部在强夯作用下的压实度变化规律，并绘制压实度随夯击次数变化的曲线，如图9所示，可以看出在不同单击夯击能的强夯作用下，夯点下方路堤底部的土体的压实度均随着夯击次数的增加而增大，超过一定夯击次数后，压实度增加幅度逐渐变缓，并趋于稳定。以6000 kN∙m夯击能的工况为例，夯击8次后，路堤底部的压实度达到由80%增大到86.9%，此后增加夯击次数，该处的压实度无明显增大，当夯击15次后，路堤底部的压实度仅达到89.1%。由此可见，对于一定的单击夯击能，其有效加固的深度是有限的。若目标加固深度较大，必须考虑采用较高的单击夯实能，并根据现场工况确定夯击次数，从而达到有效加固的效果。

Figure 9. Curve of compaction degree-times of tamping at the bottom of embankment

图9. 路堤底部压实度–夯击次数曲线

根据图8中不同能级强夯作用下的夯击次数与夯沉量对应关系，可得到累计夯沉量与累计夯击能的关系曲线，如图10所示。在不同单击夯击能的强夯作用下，夯沉量随累计夯击能的增加而增加，每增加一定的夯击能，夯沉量的增长量逐渐减少。对于不同的单击夯击能，达到同一夯沉量所需要的累计夯击能是不同的，单击夯击能越高，所需累计夯击能越低。但当单击夯击能超过一定值后，不同单击夯击能强夯作用下，达到同一夯沉量所消耗的累计夯击能基本持平。

Figure 10. Cumulative tamping capacity-cumulative tamping energy curve

图10. 累计夯沉量–累计夯击能关系曲线

工程中，强夯施工的难易程度与单击夯击能的大小成正比，在满足加固效果的前提下，应尽可能选择更低的强夯能级。前文已得出对于8 m高松铺粉土路堤，在6500 kN∙m、7000 kN∙m和7500 kN∙m能级的强夯作用下，均可得到有效加固。图10中，达到同一夯沉量(加固效果)时，6000 kN∙m、6500 kN∙m、7000 kN∙m和7500 kN∙m能级强夯消耗的总能量依次降低，7000 kN∙m和7500 kN∙m能级的强夯消耗的总能量基本持平。综合考虑消耗的总能量和施工难易程度两个因素，最终选择7000 kN∙m作为8 m高松填粉土路堤强夯填筑的最佳单击夯击能，对应的夯击次数为14击。该参数将用于路堤的多点夯模拟，进而确定最佳夯间距及其他设计参数。

2) 多点夯分析

根据8 m高度松填路堤单点夯计算分析的结果，多点夯击模型选用参数如表4所示。8 m路堤多点夯击模型设置A、B、C、D四个夯击点位，夯击次序为A→B→C→D，其他设置与单点夯击模型相同，如图11所示。选取测点1# (AD中点)、测点2# (对角线CD中点)进行分析。

Table 4. Multi-point ramming process parameters of 8 m embankment

表4. 8 m路堤多点夯击工艺参数

图11. 有限元模型及网格化分

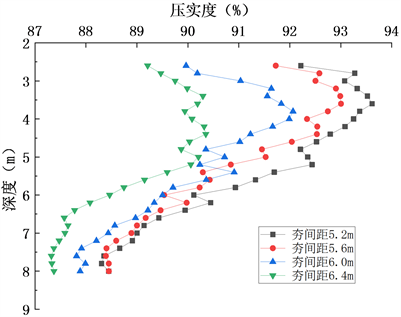
Figure 12. Compactness distribution along depth direction at measurement point 1#

图12. 测点1#压实度沿深度方向的分布

由图12可以看出，1#测点各深度处的压实度均随夯间距的减小而增大，且路堤上部的压实效果优于路堤下部。在5.2 m、5.6 m、6.0 m、6.4 m的行间距条件下，1#测点沿深度方向的最大压实度分别达到93.7%、93.0%、92.1%、90.3%。最小压实度分别为88.1%、88.2%、87.8%、87.4%。

计算不同夯间距条件下1#测点沿深度方向的平均压实度，并绘制点线图如图13所示。可以看出，1#测点沿深度方向的平均压实度与夯间距近似呈线性关系，可通过调整夯间距对路基平均压实度进行有效提高，从而提高强夯加固效果。

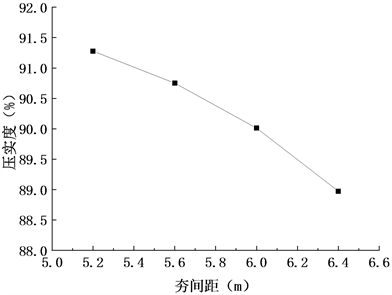
Figure 13. Average compactness-ramming point spacing curve at measuring point 1#

图13. 测点1#平均压实度—夯点间距曲线

8 m高松填粉土路堤在不同夯点间距条件下，2#测点处的压实度沿深度方向的分布如图14所示。可以看出，2#测点各深度处的压实度均随夯间距的减小而增大，且路堤上部的压实效果明显优于路堤下部。在5.2 m、5.6 m、6.0 m、6.4 m的行间距条件下，1#测点沿深度方向的最大压实度分别达到84.9%、86.3%、88.2%、90.0%。最小压实度分别为83.4%、83.6%、85.9%、87.8%。相较1#测点，2#测点压实度沿深度方向的分布更加均匀，但压实度更低，这说明2#测点处的路堤强夯加固效果较为薄弱。

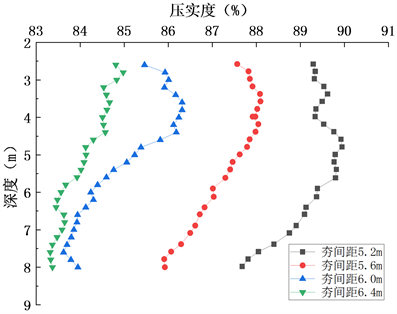
Figure 14. Compactness distribution along depth direction at measurement point 2#

图14. 测点2#压实度沿深度方向的分布

Figure 15. Average compactness-ramming point spacing curve at measuring point 2#

图15. 测点2#平均压实度—夯点间距曲线

计算不同夯间距条件下2#测点沿深度方向的平均压实度，绘制点线图如图15所示。可以看出，2#测点沿深度方向的平均压实度与夯间距也近似呈线性关系。汇总8 m高松填粉土路堤在不同夯点间距条件下，各测点平均压实度。结果表明，当夯点间距为5.2 m时，测点1#平均压实度为91.3%，测点2#的平均压实度为89.3%，基本符合90%压实度的有效加固范围判断标准，因此8 m高度粉土路基强夯加固设计参数可选择7000 kN∙m的单击夯击能、最优夯点间距为5.2 m，夯击次数14次。

4. 结论

1) 所采用的数值模拟方法通过编写子程序可实现土体模量、密度、粘聚力d、摩擦角β随夯击次数的动态变化，并根据这些指标的动态变化分析强夯加固效果，对于山东黄泛区粉土路堤的强夯加固具有较好的适用性。

2) 对4 m高粉土路堤强夯加固开展室外试验并使用有限元模型进行验证，以路堤底部达到90%压实度为有效加固指标，采用1500 kN∙m夯击能、夯点间距3.2 m、夯击10次可对该高度粉土路堤进行有效加固。

3) 以路堤底部达到90%压实度为路堤有效加固控制指标，对8 m高度松填粉土路堤进行有效加固，6500 kN∙m、7000 kN∙m、7500 kN∙m三种夯击能的有效夯击次数分别为15击、14击、13击，优选最佳单击夯击能为7000 kN∙m。

4) 若以达到90%压实度的加固区域作为路堤强夯的有效加固范围，则8m高度松填粉土路堤的建议强夯设计参数为：夯击能7000 kN∙m、夯间距5.2 m、夯击次数14次。