理想线弹性体的泊松比

Poisson’s Ratio of Ideal Linear Elastomer

摘要: 小变形下，基于体积不变假设，材料的泊松比上限为0.5，在大变形下材料泊松比的取值鲜有讨论。通过建立理想线弹性体的弹簧模型，认为体积比和泊松比均为拉伸比的独立变量，和应力模式无关。在大形变过程中，体积是变化的，变化趋势取决于初始泊松比的大小。泊松比的取值范围是(0, ∞)。当初始泊松比小于0.5时，拉伸时体积先增加后减小，压缩时体积减小；当初始泊松比大于0.5时，拉伸时体积减小，压缩时体积先增大后减小；当初始泊松比等于0.5时，拉伸或压缩时体积均减小。因此理论上应存在压缩体胀和拉伸体缩的超材料。

Abstract: Under small deformation, based on the assumption of constant volume, the upper limit of Poisson’s ratio is 0.5. Under large deformation, the value of Poisson’s ratio is rarely discussed. By establishing the spring model of ideal linear elastomer, it is considered that the volume ratio and Poisson’s ratio are independent variables of tensile ratio and independent of stress mode. In the process of large deformation, the volume changes, and the change trend depends on the initial Poisson’s ratio. The range of Poisson’s ratio is (0, ∞). When the initial Poisson’s ratio is less than 0.5, the volume in-creases first and then decreases in tension and decreases in compression; When the initial Poisson’s ratio is greater than 0.5, the volume decreases in tension and increases first and then decreases in compression; When the initial Poisson’s ratio is equal to 0.5, the volume decreases in tension or compression. Therefore, in theory, there should be metamaterials with compressive volume expan-sion and tensile volume contraction.

1. 引言

在材料力学中，泊松比的取值范围曾引起长期的广泛讨论 [1] [2]，通常认为理想线弹性体的泊松比的范围是(−1, 0.5]，潜在的假设是在拉伸情况下，材料体积不可能减小 [3]。该结论是在小变形假设下，基于广义胡克定律展开的。在大变形情况下，适应性较差，因此诞生了很多修正理论 [4] [5] [6]。

泊松比取值范围的拓展，目前主要集中在负值极限的研究 [7]，对正值极限较少涉及。仅有部分学者认为泊松比在某些特殊条件 [8] [9] 下可能大于0.5。同时，目前的研究对塑性形变的泊松比较为关注，很少有对弹性体在大变形下的泊松比进行讨论。

理想线弹性体的性质是弹性力学的理论基础，目前的弹性力学主要结论均在小变形下的理想线弹性体基础上建立，大变形下，体积不变的假设是不成立的，因此带来的弹性力学的规律会有极大的不同，泊松比就是其中一个关键因素。通过对大变形下理想线弹性体的分析，认为泊松比会突破0.5的上限，因此为设计新型的超材料提供了理论基础。

2. 体积比和泊松比

一个均质的各项同性材料，在受到一个轴向应力的作用，在该应力方向上产生伸长，其拉伸比为：

${\lambda }_x=\frac{l}{l_0}$ (1)

定义工程应变 [10] 为：

${\epsilon }_x=\frac{\Delta l}{l_0}={\lambda }_x-1$ (2)

泊松比为工程应变下的横向应变和纵向应变的比的负值 [11]：

$\nu =-\frac{{\epsilon }_y}{{\epsilon }_x}=-\frac{{\lambda }_y-1}{{\lambda }_x-1}$ (3)

因此有体积比：

${\lambda }_V=\frac{V}{V_0}={\lambda }_x{\lambda }_y^2={\lambda }_x{\left[1-\nu \left({\lambda }_x-1\right)\right]}^2$ (4)

公式(4)中有三个变量，如果我们将拉伸比看成自变量，体积比和泊松比是因变量，三个变量维持方程平衡，有无数个解，因此，拉伸比–泊松比或拉伸比–体积比应该有第二个约束条件，才能维持解的唯一性。

3. 理想线弹性体模型

弹簧模型是最常用的理想线弹性体模型，如图1，建立一个圆柱型弹簧的模型。

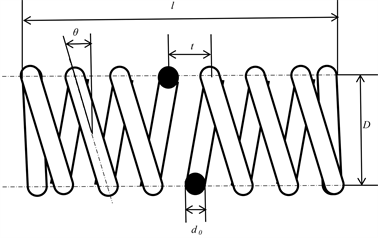
Figure 1. Schematic diagram of ideal linear elastomer spring model

图1. 理想线弹性体弹簧模型示意图

设弹簧节数为n，丝径d₀，螺旋线升角θ，弹簧总长度为L，则弹簧中径 $D=\frac{L\cos \theta }{\pi n}$，弹簧有效长度 $l=L\sin \theta$ [12]。弹簧受力后，设总长度L维持不变，因此拉伸比：

${\lambda }_x=\frac{l}{l_0}=\frac{\sin \theta }{\sin {\theta }_0}$ (5)

径向变形比：

${\lambda }_y=\frac{D}{D_0}=\frac{\cos \theta }{\cos {\theta }_0}$ (6)

由弹簧围成的空腔体积的体积比：

${\lambda }_V=\frac{\sin \theta {\cos }^2\theta }{\sin {\theta }_0{\cos }^2{\theta }_0}={\lambda }_x\left[1-{\tan }^2{\theta }_0\left({\lambda }_x^2-1\right)\right]$ (7)

弹簧模型下的泊松比为：

$v=-\frac{\cos \theta /\cos {\theta }_0-1}{{\lambda }_x-1}=\frac{1-\sqrt{1-{\tan }^2{\theta }_0\left({\lambda }_x^2-1\right)}}{{\lambda }_x-1}$ (8)

工程上材料的泊松比是指在小变形下的泊松比，即 ${\lambda }_x$ 趋近于1时的数值，我们定义为初始泊松比 ${\nu }_0$ ：

${\nu }_0=\underset{{\lambda }_x\to 1}{\lim }\frac{1-\sqrt{1-{\tan }^2{\theta }_0\left({\lambda }_x^2-1\right)}}{{\lambda }_x-1}={\tan }^2{\theta }_0$ (9)

由于 ${\theta }_0\in \left(0,\text{π}/2\right)$，因此 ${\nu }_0\in \left(0,\infty \right)$。公式(7) (8)也可写作：

${\lambda }_V={\lambda }_x\left[1-{\nu }_0\left({\lambda }_x^2-1\right)\right]$ (10)

$v=\frac{1-\sqrt{1-{\nu }_0\left({\lambda }_x^2-1\right)}}{{\lambda }_x-1}$ (11)

公式(10) (11)显示，理想线弹性体的体积比和泊松比均为拉伸比的独立函数，这三个变量均为形变变量，和应力模式无关。因此公式(4)才具备唯一解。

4. 结果和讨论

4.1. 泊松比的取值范围

从公式(11)可知，对于理想线弹性体，泊松比随着拉伸比的增加而增加，当 ${\lambda }_x$ 趋近于0时，泊松比有最小值：

$v_{\min }=\sqrt{1+{\nu }_0}-1$ (12)

当 ${\lambda }_x=\sqrt{\frac{1}{{\nu }_0}+1}=\frac{1}{\sin {\theta }_0}$ 时，泊松比有最大值：

${\nu }_{\max }=\frac{1}{\sqrt{1/{\nu }_0+1}-1}$ (13)

由于 ${\nu }_0\in \left(0,\infty \right)$，因此理想线弹性体泊松比取值范围是 $\nu \in \left(0,\infty \right)$。

对于理想线弹性体，人们通常认为泊松比不会大于0.5，但也有很多文献显示了初始泊松比大于0.5的实例 [13] [14] [15]，目前缺乏相应的理论解释，或归结为试验数据偏差 [16] [17]。泊松比上限0.5的设定，是在体积不变的假设下推出的，而在大变形下，理想线弹性体的体积比不再是常数，因此泊松比可能远远超出0.5的限制。

对于弹簧模型的理想线弹性体，初始泊松比取决于弹簧的螺旋线升角，螺旋线升角是个纯物理形状因素，因此初始泊松比大于0.5的实体应是存在的，制造是可行的。

4.2. 弹性极限

当弹簧被完全拉直时，意味着弹性的丧失。由式(5)可知，弹簧存在极限拉伸比，因此理想线弹性体的弹性极限 ${\sigma }_e$ 满足：

${\sigma }_e=E\left({\lambda }_{\max }-1\right)=E\left(\frac{1}{\sin {\theta }_0}-1\right)$ (14)

结合式(9)，可建立弹性极限和初始泊松比的关系：

${\sigma }_e=E\left(\sqrt{\frac{1}{v_0}+1}-1\right)$ (15)

公式(15)显示，对于理想线弹性体，弹性极限对应的极限应变是由初始泊松比决定的，理论上存在通过测定弹性极限和弹性模量求解初始泊松比的可能。

4.3. 体积模量

经典理论中体积应变 [11]：

${\epsilon }_v={\lambda }_V-1=\left(1-2v\right)\left({\lambda }_x-1\right)$ (16)

是在略去高阶微量后得出的结果，仅适用于小变形状态，由公式(4)、(11)可得，大变形下的体积模量K为：

$K=\frac{{\sigma }_m}{{\epsilon }_V}=\frac{E}{3\left[1-2\nu {\lambda }_x+{\nu }^2{\lambda }_x\left({\lambda }_x-1\right)\right]}=\frac{E}{3\left[1-{\nu }_0{\lambda }_x\left({\lambda }_x+1\right)\right]}$ (17)

当 ${\lambda }_x$ 趋近于1时，有初始体积模量：

$K_0=\underset{{\lambda }_x\to 1}{\lim }K=\frac{E_0}{3\left(1-2{\nu }_0\right)}$ (18)

理想线弹性体的弹性模量E为常数，因此在大变形下，体积模量不再是定值，而是随着拉伸比的变化而变化，变化趋势取决于初始泊松比 ${\nu }_0$。

4.4. 单轴应力下的体积变化

对公式(10)进行微分并令 ${{\lambda }^{\prime }}_V=0$，可得：

${\lambda }_x=\sqrt{\frac{1+{\nu }_0}{3{\nu }_0}}=\frac{1}{\sqrt{3}\sin {\theta }_0}$ (19)

由式(19)可知，当 $v=0.5$，或 $\sin \theta =1/\sqrt{3}$ 或 $\theta ={35.26}^{\circ }$ 时，弹簧有最大体积：

$V_{\max }=\frac{2}{3\sqrt{3}}\frac{{\left(1+v_0\right)}^{1.5}}{v_0^{0.5}}{V}_0\equiv \frac{2\sqrt{3}}{9\text{π}}\frac{L^3}{n^2}$ (20)

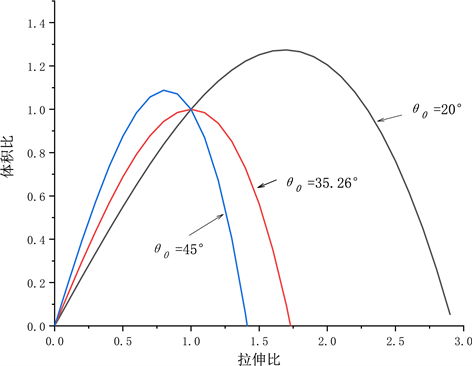
Figure 2. Volume ratio trend at different initial rise angles

图2. 不同初始升角时体积比趋势

如图2所示，当 ${\theta }_0<{35.26}^{\circ }$ 时，拉伸状态下体积先增加后减小，压缩状态下体积减小；当 ${\theta }_0={35.26}^{\circ }$ 时，拉伸和压缩状态下体积均减小；当 ${\theta }_0>{35.26}^{\circ }$ 时，拉伸状态下体积减小，压缩状态下体积先增加后减小。

${\theta }_0={35.26}^{\circ }$ 对应的初始泊松比v₀为0.5，对于大部分物质，初始泊松比均小于0.5，因此在拉伸情况下体积先增加后减少，压缩情况下体积减小，这一规律和常识相符合。当初始泊松比大于0.5时，理想线弹性体的体积变化会和常识相左。

通过对初始泊松比的设计，理想线弹性体可以成为拉伸体胀、压缩体胀或拉压体缩等不同表现的特异性材料，这为设计超材料奠定了理论基础。

5. 结论

1) 理想线弹性体的体积比是变动的，其趋势取决于初始泊松比的大小。

2) 理想线弹性体的泊松比范围为(0, ∞)。

3) 理想线弹性体的体积比和泊松比均为拉伸比的独立函数，和应力模式无关。