1. 引言
大跨越工程是一项特殊的工程,类似于铁路工程中的桥梁和涵洞工程,其重要性非常明显。因为它跨越河流、湖泊和海湾,导线挂点高、所处地形开阔,极易形成微风振动,其振动水平也较常规档距更为严重。长期的微风振动可能导致绞线断裂,严重威胁输电线路的安全 [1]。同时由于项目施工期间要封江断航,可能会对运输和航运产生很大影响,需要多个管理部门的协调。为了减少大跨越施工对各方面的影响,确保导线的安全运行,导线的防振工作应非常慎重 [2]。
亚马逊河大跨越是LT 230 kV (CD) Oriximiná-Juruti工程的一个重要组成部分,该项目所使用的AACSR/UGS 540型钢芯铝绞线在国内无应用先例,其钢比 [3] 为0.448,导线的平均运行应力(everyday stress,简称EDS)高达24%的极限抗拉强度(Ultimate tension Stress,简称UTS),而目前我国常用的大跨越导线的钢比一般小于0.3,EDS约为20%,大大提高了亚马逊河大跨越导线防振的难度。另一方面,导线微风振动是一个非线性动力学问,通过理论计算很难得到准确的计算结果。需要将理论计算和模拟试验相结合,才能得到可靠的减振措施,本文针对亚马逊河大跨越所用的AACSR/UGS 540型导线进行了防振试验设计,提出了一种新的防振形式,并经过试验验证了其有效性。
2. 工程信息和试验
2.1. 工程信息
本工程跨越方式为耐–直–直–耐,跨越档距为575 m~2355 m~550 m,如图1所示,导线采用一根AACSR/UGS 540型钢芯铝绞线,导线具体信息如表1所示。
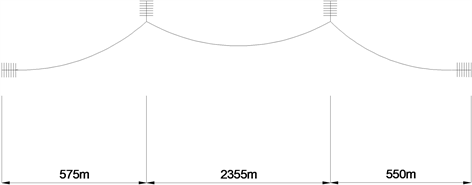
Figure 1. Crossing span s of the project
图1. 工程跨越档距
Table1. Conductor parameters
表1. 导线参数
2.2. 试验系统
在实验室利用模拟试验档对导线进行了微风振动试验。试验系统如图2所示。导线的一端与力传感器连接,另一端由液压加载装置(图中所示的张拉端)拉动以加载导线。当达到预定张力时,锁定加载装置。架设导线后,通过使用振动台在导线加载装置端部对其施加正弦激振力模拟导线微风振动。
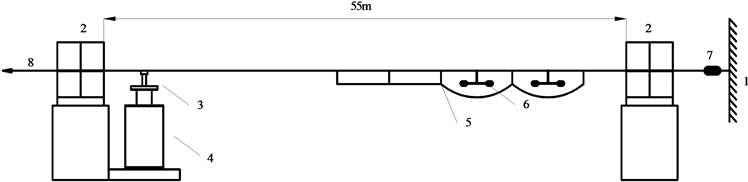 1 固定端2 重型线夹3 连接金具4 振动台5 Bate阻尼线6 防振锤 7 力传感器8 张拉端
1 固定端2 重型线夹3 连接金具4 振动台5 Bate阻尼线6 防振锤 7 力传感器8 张拉端
Figure 2. Schematic diagram of test device
图2. 试验装置示意图
2.3. 传感器布置
加速度传感器用于测量振动台附近导线第一自由半波的波腹振幅 [4],使用应变片测量图2右端夹具出口处导线的动态弯曲应变。应变片粘贴在导线上方最外层的两根线股上,如图3所示。
2.4. 试验操作
导线的振动频率由闭环控制系统控制,输入导线的功率(Pt)通过测量激振力(F)和速度(V)来控制。功率可描述如下 [5]。
(1)

Figure 3. Strain sensors on the conductor at the end
图3. 应变片在导线端部的粘贴方式
其中φ是F和V之间的相位角。试验的具体操作步骤如下:
1) 以15 Hz的振动频率激振架设好的导线,利用振动台向导线输入五个不同的能量(按从小到大的顺序,如2 W、4 W、8 W、16 W和32 W等),使导线产生不同强度的振动;
2) 记录不同振动强度下导线的振幅和各个线夹夹固点的应变;
3) 改变导线振动频率并重复(1)~(2)操作步骤。频率变化步长约为5 Hz,直至频率为65 Hz左右;
4) 整理功率、振幅和应变数据,待下一步使用。
3. 试验分析方法和试验结果
通常使用导线各线夹夹固点的最大动弯应变随频率的变化规律来表征导线的频率响应特性,包括不加任何防振装置的导线自阻尼特性和加装防振装置的导线系统特性。导线的频率响应特性可通过能量平衡法计算得到 [6] [7]。如图4所示,Pw是风能(mW/m),Pc是导线自身阻尼消耗的能量(mW/m),Pd是导线上阻尼装置消耗的能量(mW/m),Y是波腹振幅(m),D是导线直径(m)。在测试过程中,当Pt完全被导线自身消耗时,导线系统的频率响应特性即为导线自阻尼特性。当导线上安装有阻尼装置时,即Pt = Pc + Pd,导线系统的频率响应结果则可以用来评价导线系统的防振性能。
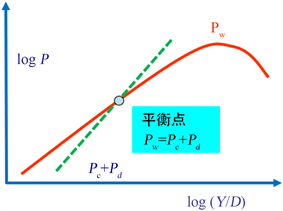
Figure 4. The sketch of energy balance method
图4. 能量平衡法示意
3.1. 导线自阻尼特性
导线的自阻尼功率用式(2) [8] 表示,
(2)
其中系数α、β是f的函数,f是导线振动频率(Hz)。式(2)两边取对数,可得:
(3)
式(3)中logPc是log(Y/D)的线性函数,α为斜率,β为截距。利用最小二乘法和试验中测得的振幅数据,可以计算出每个频率下的相应系数α和β。本工程中导线的系数α和β可描述如下:
(4)
(5)
由风能曲线和自阻尼功率曲线的交点可以计算得到能量平衡点的振幅,即“平衡点振幅”。导线自阻尼特性可以通过平衡点振幅和试验中测得的各夹固点最大动弯应变及振幅数据,利用回归计算方法拟合得到。
导线微风振动易发风速范围为0.5~10 m/s,微风振动频率和风速的关系 [9]:
(6)
式(6)中f为风对导线的激振频率(Hz),K为斯托罗哈常数(通常取0.185~0.2),v为风速(m/s),d为导线直径(m)。
导线自阻尼特性一般遵循的规律为:随着振动频率的增加,导线最大动弯应变先增大然后再减小,最大应变一般发生在20~35 Hz之间。AACSR/UGS 540型导线的自阻尼特性如图5所示。根据式(6)可计算得到该导线微风振动易发频率范围为3~55 Hz,但该导线当频率为65 Hz时,最大动态弯曲应变仍接近200 με,比标准值100 με [10] 高出约100%,显然该导线需要防振的频带较宽。
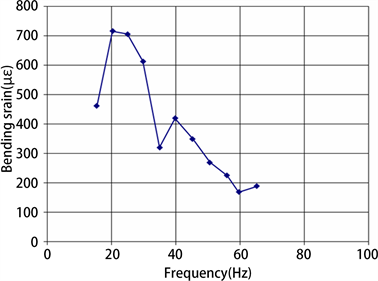
Figure 5. Self-damping characteristics of conductor AACSR/UGS 540
图5. AACSR/UGS 540型导线自阻尼
3.2. 导线系统特性
根据导线的自阻尼特性计算结果,防振锤型号选定为FR-14NL/52和FR-8NL/52。根据国内相关试验经验,Bate阻尼线型号选定为JL/G1A-630/45。根据微风振动频率的上限(65 Hz)和下限(15 Hz),初始防振装置的设计图如图6所示。
导线系统特性的计算方法与自阻尼特性的计算方法相似。在计算导体自阻尼特性时,测试功率Pt由导线自身消耗,即,
(7)
导线系统消耗的功率则为:
(8)
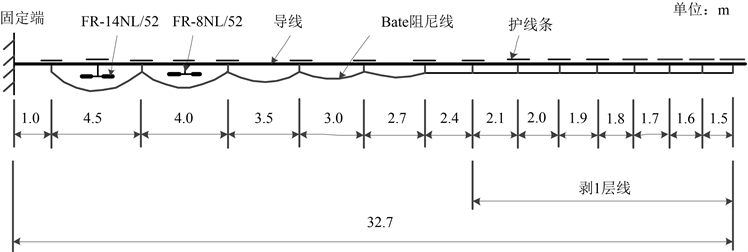
Figure 6. Initial combined anti-vibration device diagram
图6. 初始联合防振装置图
用上述方法可以得到导线系统特性。
国内通常在某档导线两端安装各一套联合防振(即Bate阻尼线 + 防振锤)装置。然而,由于亚马孙河大跨越工程中使用的导线钢比较大,且只架设了一根导线,因此防振试验的难度大大增加,安装初始防振装置的导线频率响应如图7所示,与标准要求还有很大差距。
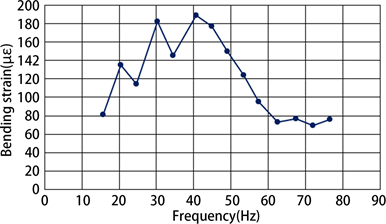
Figure 7. Frequency response of the conductor with initial combined damping device
图7. 安装初始防振装置的导线系统频响
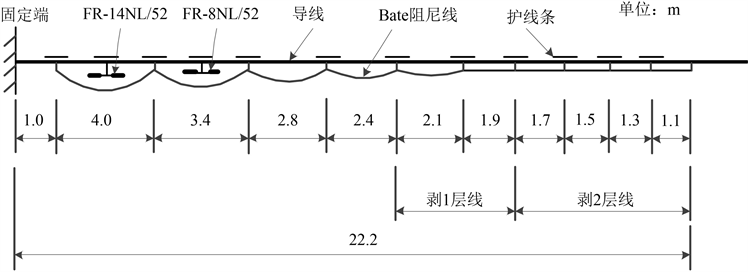
Figure 8. Diagram of combined anti-vibration device
图8. 联合防振装置图
为解决上述问题,将该2355 m档距平均分为两段,将两段作为独立的档距进行防振方案的设计。根据图7中的频率响应测试结果,改变对应于导线20~55 Hz频段的阻尼线的长度或直径,通过试验及其结果对防振装置逐步进行优化,最终得出防振装置图如图8所示。与以往不同,该工程在2355 m档距中使用了四套联合防振装置。该档导线最终的防振方案如图9所示,导线系统特性如图10所示,满足了标准要求。

Figure 9. The final anti-vibration scheme of crossing section
图9. 跨越档导线最终防振方案
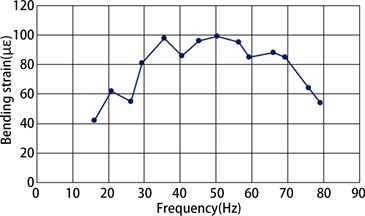
Figure 10. The frequency response of conductor with final anti-vibration scheme
图10. 安装最终防振方案的导线的频率响应
4. 结论
亚马逊河大跨越工程导线采用AACSR/UGS 540型钢芯铝合金绞线,由于这种导线的钢比大,额定拉断力高,传统的方法已不能满足标准要求。本文介绍了亚马逊河大跨越工程导线防振试验研究工作流程,提出了将跨越档等分为两段,并单独进行防振的方法,取得了良好的试验效果,为工程实践提供了参考。