高速列车受电弓弓头的降噪研究

Study on the Noise Reduction of High-Speed Train Pantograph Head

摘要: 随着高速列车的速度提升，受电弓区域产生的气动噪声快速增强，其中弓头杆件周围漩涡引起的气动噪声最为强烈。本文首先将单弓受电弓的弓头简化为有限长方柱，并针对方柱进行了一系列低噪声设计，通过大涡模拟与FW-H声学传播方程对不同方案在高速来流下产生的流场特性和远场气动噪声特性进行了分析，获得方柱远场噪声的指向性。通过对方柱添加不同半径的圆角，得到当圆角半径为20 mm时远场气动噪声最大可以降低16.8 dB；在此基础上通过对方柱进行贯通开缝，发现宽10 mm的开缝使方柱远场气动噪声进一步降低约12.8 dB。对方柱进行截面形状优化并在此基础上进行贯通开缝，能够起到明显的降噪效果，本文研究可以为受电弓的低噪声设计提供理论支撑。

Abstract: The aerodynamic noise in pantograph area increases quickly with the increase of the speed of the high-speed train, and when vortex shedding behind the rectangular cross-section panhead, it caus-es the strongest aerodynamic noise. In this paper, the panhead is simplified by a square cylinder and its far-field noise under the high-speed flow was calculated based on the Large Eddy Simulation and Ffowcs Williams/Hawkings equation. By analyzing the directivity of far-field noise and the characteristics of the flow field, a low-noise designed model is carried out. The square cylinder is preliminarily optimized by adding different radii of fillets, which causes the maximum sound pres-sure level of the far-field noise generated by the square bar is maximum reduced by 16.8 dB when the fillet radius is 20 mm, and the effect of slotting on the aerodynamic noise is further studied. It shows that with the through slits of different widths, when the width is 10 mm the maximum sound pressure level is further more reduced by 12.8 dB. In this paper, the design of optimizing the sec-tion shape and slitting has a good effect on reducing the aerodynamic noise generated by square cylinder is proved, and it provides a theoretical support for further studies on the reduction of the aerodynamic noise of the pantograph.

1. 引言

随着高速列车的发展，低噪声设计已经成为更高速度级列车外形设计的关键指标 [1]，当高速列车的运行速度达到300 km/h以上时，气动噪声在所有噪声中的占比达到50%以上。Sun [2] [3] 等通过NLAS方法计算列车主体部位的气动噪声，确立了高速列车的关键噪声源，受电弓暴露在列车顶部，组成其结构的各个杆件与高速来流的相互作用不可避免。受电弓表面的压力脉动形成偶极子声源，其强度与速度的六次方成正比，受电弓部位产生的气动噪声占据了主导地位 [4]，严重影响到了列车内乘客的舒适性，因此降低受电弓区域的气动噪声非常重要。

受电弓气动噪声的产生与漩涡脱落密切相关。由于柱体表面的阻滞作用，气流流经杆件时在其下游会形成卡门涡街，湍涡不断生成与脱落，导致压力脉动。因而，抑制受电弓气动噪声的关键在于控制关键部位杆件下游涡的产生与脱落。

目前针对受电弓部位杆件绕流引起的气动噪声，国内外大量学者对受电弓的气动噪声特性、不同杆件的气动噪声贡献量以及相关的降噪方法等进行了详细研究。姚永芳 [5] [6] 在对某高速受电弓进行350 km/h速度下的气动噪声分析后发现受电弓的升降状态、底座的特征与导流罩壁板影响了气动噪声的频谱特性与强度。Zhang [7] 则发现在组成受电弓的多个杆件中，弓头对气动噪声的贡献量最大，平衡臂和弓头支架次之。Dai [8] 在对双弓头结构的受电弓进行计算后得出，位于前方的弓头杆件将影响后方杆件的气动表现；而Li [9] 的研究则指出弓头间的间距也影响了远场气动噪声的强度。针对弓头杆件进行低噪声设计是降低受电弓气动噪声的最有效手段，对于其他杆件绕流的研究也具有参考价值。

针对杆件进行低噪声设计，国内外学者也进行了大量研究工作。侍荣春 [10] 通过大涡模拟对圆柱绕流进行模型计算，发现对杆件表面做类高尔夫球表面的球缺型凹坑处理能够有效降低气动噪声的声压级，且凹坑布置越密集，降噪效果越好；并在另一项研究 [11] 中指出增加适当尺寸的圆角能够使方柱产生的气动噪声大幅度降低，且降噪效果与圆角半径尺寸呈现非线性关系。Sueki [12] 的风洞试验证明：使用合适的多孔材料能够有效降低气动噪声在宽频范围的强度，在360 km/h的风洞试验运行下，杆件产生的气动噪声减小了1.9 dB。刘海涛 [13] 对比长耳鸮与潮间带贝壳两种生物的典型仿生结构，得出模拟潮间带贝壳的环状波纹结构模型对椭圆形结构具有明显的降噪减阻效果。王俊娇 [14] 等研究了周期性凸起结构对圆柱绕流流场及声场的影响得出，周期性凸起结构能够明显降低圆柱绕流的涡脱落噪声，且凸起结构的直径越大，降噪效果更为显著。

上述研究表明改良受电弓杆件形状能够起到一定的降噪作用，本文进一步进行了拓展，提出对杆件添加圆角、对杆件贯通开缝的处理方法，对横截面边长为0.1 m的方柱进行低噪声设计，为受电弓弓头的降噪提供了参考。

2. 计算模型与方法

2.1. 研究对象及简化

图1为某型受电弓弓头部位的简化模型 [15]，其中弓头杆件的横截面近似为矩形。

Figure 1. Simplified pantograph model

图1. 受电弓简化模型

为详细研究弓头关键外形的降噪设计，本文将弓头简化为边长0.1 m，展长0.3 m的方柱，如图2(a)所示。数值建模上，如图2(b)所示，给出了整体计算域。以杆件中心位为原点，计算域满足边界条件对流场没有影响的要求，三个方向的长度分别为来流方向7 m，宽度方向与杆件展向同为0.3 m，高度方向2 m。设置计算域前后、上下侧面的边界均为自由流边界条件，取列车速度350 km/h为入口来流速度边界；展向方向两侧为对称边界。

为保证计算的准确性，对杆件表面及附近的网格进行加密，杆件表面的网格尺寸约为3 mm，并设置边界层15层，边界层厚度增长率为1.15，首层厚度约为0.0023 mm。最终得到杆件原型模型I的网格数量为372万。

选择方柱表面为FW-H方程的积分面，如图3所示，为获得气动噪声在远场的指向性，沿原点以半径为5 m、每隔10˚设置一个远场噪声监测点，用于计算当地的声压脉动。

2.2. 计算方法

本文采用SST $k-\omega$ 湍流模型及宽频噪声源模型对流场及声源分布进行定常计算；并将稳态计算的结果作为非定常计算的初始条件，运用大涡模拟进行流场分析，并通过FW-H方程计算远场噪声，最后经FFT变化后得到远场气动噪声的强度。

(a) 方柱几何模型示意图 (b) 外流场尺寸及网格加密区

Figure 2. Sketch of the geometry and computation domain

图2. 几何模型及计算域

Figure 3. Position of the FW-H receivers

图3. FW-H接受点布置图

空间滤波得到的大涡模拟模型的连续方程、动量方程分别为：

$\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x_i}\left(\rho {\bar{\mu }}_i\right)=0$ (1)

$\frac{\partial }{\partial t}\left(\rho {\bar{\mu }}_i\right)+\frac{\partial }{\partial x_j}\left(\rho {\bar{u}}_i{\bar{u}}_j\right)=-\frac{\partial \bar{P}}{\partial x_i}+\frac{\partial }{\partial x_j}\left(\mu \frac{\partial {\bar{u}}_i}{\partial x_j}\right)-\frac{\partial {\tau }_{ij}}{\partial x_j}$ (2)

式中：

$\rho$ 为流体密度；

t为时间；

$\mu$ 为湍流粘性系数；

${\bar{u}}_i$ 、 ${\bar{u}}_j$ 为滤波后得到的速度分量；

P为压力；

${\tau }_{ij}$ 为亚格子应力尺度。

取时间步长为3e−5 s进行共10,000步非稳态计算，取0.1 s至0.3 s间FW-H监测点处的声压信息进行快速傅里叶变换，获得气动噪声沿不同方向传播形成的远场噪声。

3. 数值方法校验

为验证计算网格和计算方法的准确性，本文采用与1.1相似的网格生成策略，与王毅刚 [16]、杨志刚 [17] 等在某气动–声学风洞开展的直径0.1 m、高1.8 m圆柱气动噪声实验进行了比对。

如图4所示，实验中设置主体结构高1.8 m的圆柱，为避免顶端效应，在圆柱顶部增加半径50 mm的半球结构；圆柱底部呈圆台形与地面连接。在进行仿真模拟时使用的圆柱模型与实验一致，计算域在x、y、z三个方向上的长度分别为3.5 m、1.6 m、2.8 m。最终得到的网格数量约为2300万。

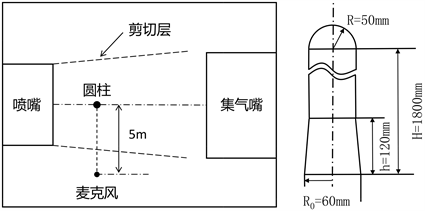
Figure 4. Wind tunnel test setup and diagram of cylinder structure

图4. 风洞实验布置及圆柱结构示意图

图5给出了原研究中在距离圆柱中心位置5 m、高1.2 m处测点的风洞测试、数值仿真以及本文数值分析得到的声压频谱比较。对比发现验证结果的低频率声压级的结果高于风洞测试，具有一定误差，但在远场气动噪声的峰值频率63 Hz处最大声压值的结果与风洞试验的测量值相匹配，为79 dB，符合圆柱绕流涡脱落的峰值特征。基于此结论，可以认为本文采用的大涡模拟与FW-H方程对柱体绕流的远场噪声强度的模拟具有较好的准确性。

Figure 5. Spectra contrast of far field noise

图5. 远场噪声频谱分析

4. 圆角对远场噪声的影响

4.1. 模型设计

通过对方形杆件的横截面形状添加半径分别为5 mm、10 mm、20 mm、30 mm的圆角，得到模型II-1、模型II-2、模型II-3、模型II-4，其横截如图6所示。

(a) 模型II-1 (b) 模型II-2 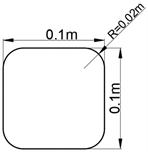(c) 模型II-3 (d) 模型II-4

Figure 6. Fillet models with different radii

图6. 不同半径的圆角模型

4.2. 流场分析

以圆角模型II-3为例，使用与模型I相同的计算域与边界条件，得到方柱模型I与圆角模型II-3流场中涡量云图如图7所示。

(a) 模型I涡量云图 (b) 模型II-3涡量云图

Figure 7. Vortices on the symmetry plane

图7. 对称平面上的涡量云图

可见无圆角情况下，方柱下游形成剧烈且扩散的大涡，漩涡强度大，在方柱下游左右大幅扩散。而在圆角作用下，模型II-3后方涡街更为“狭窄”，涡旋的有效影响区域大幅缩小。这是由于无圆角方柱前缘直角位置存在明显的流动分离，在拐角外侧形成分离涡，进一步拍打下游壁面产生剧烈波动；而在模型II-3中，适当的圆角处理使得杆件表面的流动过渡更为平稳，明显减弱了对下游流场的扰动。

4.3. 远场噪声分析

如图8所示，本节给出了不同方柱模型的远场噪声指向性。

与模型I远场噪声比较，可以发现各个尺寸的圆角都能使方形杆件产生的气动噪声降低，当圆角半径尺寸在20 mm以下时，模型的降噪效果随着圆角半径的增大而加强，且偶极子声源特性逐渐增强；当圆角半径达到20 mm时，远场噪声的降低达到了最大值16.8 dB；当圆角半径超过20 mm，远场气动噪声随着圆角半径的增加而再度上升，远场噪声随圆角半径变化的非线性规律与侍容春的研究 [11] 一致。

Figure 8. Noise directivity by model II

图8. 模型II的远场噪声指向性

由此可见，对于截面边长为0.1 m的方柱，添加半径为0.02 m的圆角能够有效降低远场气动噪声的强度。

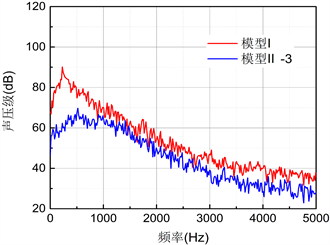
在辐射角分别为0˚、90˚的监测点位置，模型I与模型II-3的气动噪声频谱分布如图9所示。

(a) 辐射角0˚位置 (b) 辐射角90˚位置

Figure 9. Noise spectra of model I and model II-3

图9. 模型I与模型II-3的气动噪声频谱特性

可见在0˚辐射角位置，模型II-3的声压级强度在所有频率段内均明显低于模型I，声压级在500 Hz左右达到峰值，但不存在明显的特征频率，相比模型IV的220 Hz有所滞后；而在90˚辐射角位置，噪声的主要频率段内模型II-3的声压级强度低于模型I，最大声压级的降幅达到了15 dB，且峰值频率从130 Hz变为250 Hz。可以看出，适当的圆角处理能够有效降低方柱模型气动噪声的强度，在平行于来流方向上表现为使单一主峰值消失；而在垂直于来流方向上，圆角处理使声压级峰值降低并向高频方向移动。

5. 开缝对远场噪声的影响

5.1. 模型设计

基于上述结论，为进一步降低方形杆件产生的气动噪声，本文对模型II-3设计了四种不同尺寸的开缝模型如图10所示，分别命名为模型III-1、模型III-2、模型III-3、模型III-4，其开缝宽度分别为5 mm、10 mm、20 mm、30 mm。

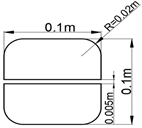(a) 模型III-1 (b) 模型III-2 (a) 模型III-3 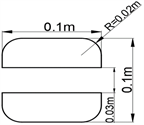(b) 模型III-4

Figure 10. Slit models with different widths

图10. 不同宽度的开缝模型

使用与模型I相同的计算条件，得到开缝模型III-1、模型III-2、模型III-3、模型III-4的流场及远场噪声计算结果。

5.2. 流场分析

图11给出了五种模型下横截面上的涡量分布云图。相比于模型II-3，开缝模型使杆件后方的涡街变得更为狭窄紧凑，当流体经过模型细缝，高速气流直接冲击到尾涡上，将大尺度涡击碎形成小尺度碎涡，呈现一定的收束效果。而当开缝宽度较大时，缝隙内表面附近的涡量较大，多股流动的相互作用使后方流场呈现出无序的复杂状态。

(a) 模型II-3涡量云图 (b) 模型III-1涡量云图 (c) 模型III-2涡量云图 (d) 模型III-3涡量云图 (e) 模型III-4涡量云图

Figure 11. Vortices on the symmetry planes of model III

图11. 模型III对称平面上的涡量云图

5.3. 远场噪声分析

如图12所示，本节同样给出了新的方柱模型的远场噪声指向性。

Figure 12. Noise directivity by model III

图12. 模型III的远场噪声指向性

可以看到，不同缝隙宽度的开缝模型的远场噪声均显示出了明显的降低，其中模型III-2的远场噪声与模型II-3相比最大降低了12.8 dB，达到了最佳的降噪效果；而当缝隙宽度大于10 mm，远场气动噪声的强度呈现出升高的趋势。由此可见，缝宽与远场噪声强度之间也呈现非常明显的非线性关系，在对方柱添加适当尺寸的圆角的基础上，进行适当尺寸的细缝能够进一步提高模型的降噪效果。至于最佳的方柱圆角半径和开缝宽度，则需要进行进一步的优化分析。

在辐射角分别为0˚、90˚的监测点位置，模型II-3与模型III-2的气动噪声频谱分布如图13所示。

(a) 辐射角0˚位置 (b) 辐射角90˚位置

Figure 13. Noise spectra of model II-3 and model III-2

图13. 模型II-3与模型III-2的气动噪声频谱特性

在0˚辐射角位置，模型III-2的远场气动噪声声压级在不同频率的分布与模型II-3存在类似的趋势，都在500 Hz左右达到一峰值，并在800 Hz左右有另一较小峰值；当频率小于3000 Hz，模型VIII-2的声压级小于模型V-3；而在更高频段两模型的气动噪声声压级近似。而在90˚辐射角位置，模型III-2的气动噪声相比模型II-3声压级随频率变化的整体规律不变，但声压级强度明显降低；仅在噪声峰值频率处，由于单一主频峰值噪声从模型II-3的峰值频率250 Hz升高至420 Hz，导致模型III-2的气动噪声稍高于模型V-3。

可见适当宽度的开缝处理能够有效降低圆角方柱模型的气动噪声，在平行于来流方向上表现为数值的降低，而在垂直于来流方向上引起声压级整体的降低与峰值频率的升高，声压级最大值的降幅明显。

6. 总结

本文将受电弓弓头简化为方柱，并提出了一系列方柱的低噪声优化设计方案，通过大涡模拟和FW-H声音传播方程研究了不同方案的流场特性和远场噪声指向性，主要结论如下：

1) 在相同来流速度下，对方柱添加不同尺寸的圆角能够降低远场气动噪声的强度。对于截面边长为0.1 m的方柱，所有方案中半径为20 mm的圆角产生的降噪效果最好，最大降幅约16.8 dB。在噪声主要频率段内，圆角处理使模型的声压级峰值减弱甚至消失，峰值频率向高频方向变化。

2) 在最佳圆角的基础上，本文提出的前后贯通的不同尺寸细缝均能够进一步降低杆件产生的气动噪声，所有方案中宽度为10 mm的细缝能够使20 mm圆角柱体杆件的远场气动噪声额外降低12.8 dB，不同辐射方向上的声压级强度都得到了明显降低。

3) 无论是进行圆角倒角还是进行贯通开缝，倒角半径、开缝宽度与远场噪声之间均存在着明显的非线性关系，最佳圆角和开缝尺寸需要采用优化的方法获取。

基金项目

国家数值工程项目(NNW2020-DY01-002)。

NOTES

^*通讯作者。