1. 引言
从新冠病毒在2019年底爆发以来,新冠病毒至今已经产生了11种变异毒株,包括我们所熟知的Alpha、Beta、Gamma、Delta等。经过各国以及各地区的基因测序抽检,发现Alpha、Delta、Delta变种(VUI-21OCT-01)变种病毒相对其余变种病毒而言,感染人数增长更加明显,感染人数总量更多。因此,我们可以通过这些病毒感染数据来计算出它们的传播速度和持续时长,从而划分疫情发展阶段。由于基因测序工作的延迟性,往往病毒已经开始传播一段时间才进行测序,所以经常无法确定病毒的确切开始时间,需要根据现有病毒传播特性以及现有数据进行反向推理。除此之外,温度、湿度与大气压等气候因素会对病毒的传播产生影响,因此,研究这些因素与新增感染人数的相关性,对预测和控制疫情发展具有很大的作用。
对于疫情感染人数的预测一直以来都是控制疫情传播的重点工作。国内外学者已经建立了许多相关预测模型,包括适用于小数据量的灰色系统预测模型 [1]、适用于大数据量的ARIMA模型 [2]、指数平滑模型 [3] 以及基于传染病动力学的SI、SIR、SIRS、SEIR模型 [4] 等。灰色系统预测、ARIMA模型和指数平滑模型都是先探索原始数据本身所具有的规律性,从而对未来的发展趋势进行预测,忽视了病毒本身所具有的传播规律。而SEIR模型等则是根据传染病传播和染病的过程将人群分类,从而构建相应的微分方程进行模拟,需要知道病毒实际的治愈率、致死率等数据,要求较高。
通过分析本文数据,发现已知数据类型仅有病毒感染总人数一种数据,所以传染病动力学模型并不适用。除此之外,已知的感染数据大多数都是病毒传播的中后期数据,感染总人数增长逐渐停止,因此使用灰色预测或ARIMA模型向后预测意义不大。考虑实际情况中,病毒传播的前期没有及时进行干预,病毒增长不受控制,增速较快。而在中后期,感染者中的部分被治愈而获得抗体,加上政府开始实施防疫措施,病毒的增速逐渐下降直至停滞。所以,我们可以类比人口增长 [5] 和种群增长 [6],在已知病毒的传播特性和数据存在缺失且类型单一的情况下,采用Logistic增长模型 [7] 对病毒传播过程进行模拟,从而预测病毒的开始时间和初期传播情况。
2. 数据来源
本文通过英国新冠疫情官方统计网站,英国政府官方网站公开发布的信息,获取了英国全国以及379个地区2020年2月1日至2022年3月31日每日新增病例数据以及这379个地区在这段时间内每日的温度、露点(一个气象学概念)、湿度、风速、压强数据。通过英国政府发布的每日基因测序抽检结果,得到了自2021年5月20日开始统计至2022年3月31日期间每周的Alpha、Delta、Delta变种(VUI-21OCT-01)的病毒感染数量增长数据。获得的数据时间跨度广,总体质量高,可靠性强。
3. 模型假设
3.1. 模型的假设
· 病毒感染的总人数数据连续;
· 不同病毒之间存在竞争关系;
· 英国人口总数维持基本恒定,即出生率等于死亡率;
· 新冠病毒及其变种的感染速度受环境因素和已感染人数影响,且存在上限;
· 某种病毒感染人数至上限时,未来将不会继续传播。
3.2. 符号说明
——时间;
——Alpha病毒、Delta病毒、Delta变种病毒的固有增长率;
——Alpha病毒、Delta病毒、Delta变种病毒感染总人数;
——Alpha病毒、Delta病毒、Delta变种病毒感染增长率;
——Alpha病毒、Delta病毒、Delta变种病毒最大感染人数;
——Alpha病毒、Delta病毒、Delta变种病毒感染初始时间;
——Alpha病毒、Delta病毒、Delta变种病毒感染初始感染数。
4. 模型的建立、求解和分析
4.1. Logistic增长模型
由于英国政府在疫情持续了一段时间之后才开始对大众进行基因测序抽检,所以目前我们仅能掌握每种病毒一段时间内的感染人数数据,无法判断病毒开始的传播的时间、持续时间以及目前病毒传播的阶段。考虑到病毒的增长受到环境中人口数量、人口密度、气候等因素的影响,随着感染数量的增加,感染速度将逐渐缓慢,直到感染数量到达上限时,增长完全停止。根据Logistic增长模型 [7],病毒感染率
会随着人口数量
的增长而下降。我们不妨设
为
的线性减函数,即:
(1)
为病毒的固有增长率,表示感染初期(
时)感染人数很少时的增长率。根据假设,当达到最大感染数量
时,病毒不会继续传播,则
,
,从而:
(2)
建立感染人数Logistic增长模型的微分方程组:
(3)
对其分离变量进行求解:
代入初值条件,得到最终感染人数随时间的表达式:
(4)
根据上述结果表达式,我们可以依次求出原始病毒、Alpha病毒、Delta病毒的阻滞增长拟合曲线。由于英国全国病毒感染总人数的数据是从2020年1月30日开始的,我们不妨设这一天为
。

Figure 1. The Logistic growth curve of Alpha virus
图1. Alpha病毒Logistic增长曲线
首先考虑Alpha病毒。从已知数据来看Alpha病毒感染人数具体统计数据是从2021年5月20日开始记录的,当日总感染人数为249,637人,则
,
。为了判断Alpha病毒的开始时间,我们使用公式(4)进行拟合,编写代码对上述公式中的未知数进行最优拟合求解,最终得
,
,拟合曲线如图1所示。通过求得的感染人数表达式,代入已知数据的时间点,求出预测数据与实际数据进行对比,求得可决系数
,说明拟合优度良好。
通过图1可以看出,目前已知Alpha病毒数据属于传染后期数据。为了求得病毒开始时间,只需令Alpha病毒的Logistic增长曲线表达式
,计算得出
,推断Alpha病毒的实际开始时间为2020年8月28日左右,与新闻报道的英国首例Alpha病毒发现时间基本重合。从图1观察到,
时,感染人数不再继续上升,即可视为Alpha病毒到达感染上限。所以Alpha病毒在英国的持续时长约为350天,基础增长率为0.055。
接下来考虑Delta病毒,通过已知数据得到初值条件
,
。同上述步骤,编写程序求解,得
,
,拟合曲线如图2所示。和实际数据比较,
,说明拟合程度良好。
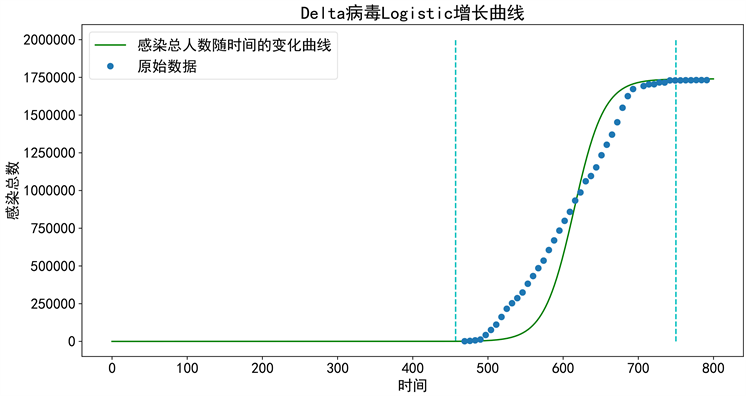
Figure 2. The Logistic growth curve of Delta virus
图2. Delta病毒Logistic增长曲线
由于Delta病毒在英国为境外输入型病毒,所以病毒的开始时间不能直接用求得的曲线表达式求出。通过查阅资料,Delta在英国的开始时间约为2021年5月1日,即
,通过图像观察Delta感染达到上限时间为
。所以Delta病毒在英国的持续时长约为293天,基础增长率为0.05。
最后考虑Delta变种病毒,通过已知数据得到初值条件
,
。同上述步骤,编写程序求解,得
,
,拟合曲线如图3所示。和实际数据比较,
,说明拟合程度良好。
根据所求得的公式,令
,求得
,推断Delta变种病毒在英国的实际开始时间为2021年6月15日左右。考虑到病毒的潜伏期,所以拟合结果基本与新闻报道的日期相符。通过观察图3,可以看出所记录的Delta变种病毒感染数据为中后期数据,感染人数到达上限时间为
。所以Delta变种病毒在英国的持续时长约为378天,基础增长率为0.075。

Figure 3. The Logistic growth curve of mutated Delta virus
图3. Delta变种病毒Logistic增长曲线
4.2. 相关性分析
接下来考虑气候因素对病毒传播速度的影响。我们不妨选择位于英格兰的曼彻斯特作为特例进行研究。根据英国官方网站的统计数据,我们获得了曼彻斯特2020年4月1日至2022年3月31日每日的新增感染人数、温度、露点、湿度、风速、压强数据。对这些变量进行Pearson相关性分析。
4.2.1. 数据的正态性检验
首先对数据的进行正态性检验。由于各变量的数据数量未超过5000,即样本为小数据样本,所以我们采用Shapiro-Wilk检验。使用SPSS进行分析 [8],绘制正态性检验直方图,见图4。
通过正态性检验结果直方图来看,各因素的图像基本上呈现出正态分布的钟形(中间高,两端低),说明虽然数据不是绝对正态,但是基本可以接受为正态分布,因此可以选择构造Pearson相关系数对各变量进行相关性分析。


Figure 4. The histograms of normality test: (a) the number of daily new cases; (b) temperature; (c) dew-point temperature; (d) humidity; (e) wind speed; (f) atmospheric pressure
图4. 正态性检验直方图:(a) 新增感染人数;(b) 温度;(c) 露点;(d) 湿度;(e) 风速;(f) 压强
4.2.2. 相关性分析
基于正态分布检验结果,我们对各变量构造Pearson相关系数。设任意两个变量之间的样本点为
,两变量的样本均值分别为
,则它们之间的Pearson相关系数可以定义为 [9]:
(5)
使用SPSS代入数据进行求解,求得两两变量之间的显著性P值以及Pearson相关系数,如下图5所示。
从表1和图5上可以看出,每日新增病例数量与温度和湿度的显著性P值均小于1%,即都具有显著性,说明两变量之间存在相关性。通过相关系数热力图可以看出,新增病例数量与温度和湿度的Pearson相关系数的绝对值相对其他变量较大,分别为−0.218和0.293,说明新增数量主要受这两个因素的影响,且与温度呈负相关,与湿度呈正相关。

Table 1. P values of each variable
表1. 各变量显著性P值
注:***、**、*分别代表1%、5%、10%的显著性水平。
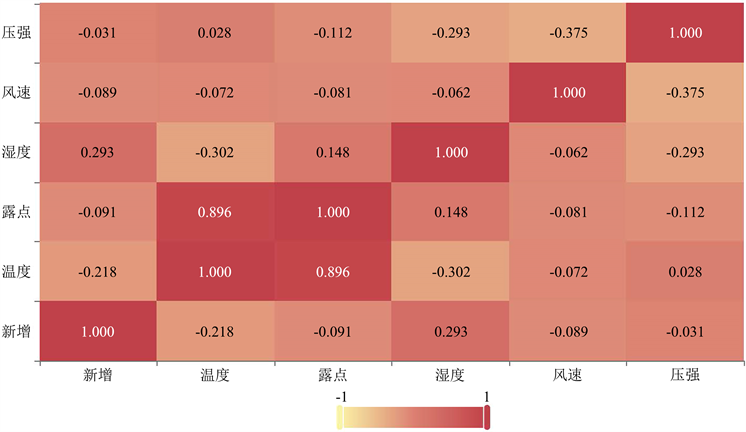
Figure 5. The heat map of Pearson correlation coefficients between each variable
图5. 各变量之间的Pearson相关系数热力图
5. 结论
本文在英国政府官网上公布的病毒感染数据基础上,通过构造Logistic增长曲线,我们求得了Alpha病毒、Delta病毒、Delta变种病毒在英国的传染总人数曲线图,分别计算出了三种病毒的基础增长率,求出了Alpha病毒、Delta变种病毒的开始时间,和新闻报道的第一例出现时间基本吻合,在此基础上求出了三种病毒各自的持续时间。选择曼彻斯特作为研究对象,通过正态性检验和构造Pearson相关系数分析温度、露点、湿度、风速、压强等气候因素与每日新增感染人数的相关性。求得每日新增人数受温度和湿度影响最大,且新增人数与温度呈负相关,与湿度呈正相关。