汽车电动制动助力器电机控制算法研究

Research on Motor Control Algorithm of Automotive Electric Brake Booster

摘要: 电动制动助力器是现代汽车的关键难点技术之一，直接关系到整车系统功能的实现，对电机控制策略的研究极为关键，目前该技术主要由国外公司掌控，自主研究该技术已成为整车厂迫切任务之一。首先，分析对比了电动制动助力器的工作机理，并将PMSM与BLDC做了对比，明确了选择矢量控制策略作为助力电机控制的主要原因。其次，分析了矢量控制策略的特点及对其控制逻辑进行了项目详细描述，对其核心部分的坐标变换和SVPWM算法进行了公式推导和数学建模，在理论上论证了该套逻辑的可行性，建立了8种开关状态与相电压和线电压的对应关系，以扇区描述了电压空间矢量图。接着，通过MATLAB/Simulink搭建了矢量控制策略的仿真模型，并将位置、速度、扭矩作为目标输入，从里到外分别以PI控制器控制电流环，速度环及位置环。最后，以仿真模型验证了电流环、速度和和位置环，其控制精度分别为99%、96%和99%，系统延迟均控制在0.02秒以内，电机幅值波动也较少，均在合理范围以内，从而验证了该仿真模型的正确性和有效性。

Abstract: Electric brake booster is one of the key and difficult technologies of modern vehicles, which is directly related to the realization of vehicle system functions. The research on motor control strategy becomes very critical. At present, this technology is mainly controlled by foreign companies and research on this technology has become one of the urgent tasks of OEMs. First of all, the working mechanism of the electric brake booster is analyzed and compared, the PMSM and BLDC are compared, and the main reason for choosing the vector control strategy as the power motor control is clarified. Second, analyzing the characteristics of the vector control strategy and its control logic is described in detail, the project of the core part of the coordinate transformation and the SVPWM algorithm formula derivation and mathematical modeling, demonstrates the feasibility of this set of logic in theory, set up eight kinds of switch state, the corresponding relationship between phase voltage and line voltage sector which is used to describe the voltage space vector diagram. Then, the simulation model of vector control strategy is built by MATLAB/Simulink, and the position, speed and torque are taken as the target input, and the current loop, speed loop and position loop are respectively controlled by PI controller from inside to outside. Finally, the simulation model is used to verify the current loop, speed loop and position loop, and the control accuracy is 99%, 96% and 99%, respectively. The system delay is controlled within 0.02 seconds, and the amplitude fluctuation of the motor is less, which is within a reasonable range, thus proving the correctness and effectiveness of the simulation model.

1. 引言

新能源智能汽车的开发已成为汽车行业的主流发展方向，而制动是保障汽车安全行驶的关键，需要高灵敏度和集成度。电动制动助力器具有体积小、集成度高、灵活度高、可实现主动建压等优点 [1]，是替代真空助力器的最佳选择。电动助力器多采用永磁同步电机(Permanent Magnetic Synchronous Machine, PMSM)合适的控制算法能有效提高助力电机的输出性能。国内外学者和工程师展开了广泛的研究。孟德智等搭建了电子助力制动系统永磁同步电机控制的硬件平台，并进行了软件程序设计，在控制策略方面，设计了转子动能为外环控制量的反馈控制策略，解决了电子助力电机调速系统转速超调的问题 [2]。赵健等提出了一种基于改进滑膜变结构控制和线性矩阵不等式的双闭环控制策略，满足了电子机械助力制动系统中的永磁同步电机位置伺服控制的高精度要求 [3]。李建涛等针对快踩制动踏板电机响应慢的问题，采用弱磁控制算法扩大电机转速，提高电机响应速度 [4]。Seungjin Y等考虑到在电机电流传感器故障的情况下，助力器将无法正常工作，提出了一种基于观测器的反馈控制器以解决此问题，并系统中采用双闭环PID控制器来控制制动系统液压，用矢量控制(Field Oriented Control, FOC)来控制永磁同步电机并进行了仿真验证 [5]。为使电动制动助力系统快速响应，Gong X等采用电流补偿解耦和最大转矩电流比控制策略(MTPA)，最终使PMSM可以在较大的速度范围内运行并保持有一定的抗负载干扰能力 [6]。

针对电动制动助力器的电机控制的应用，较少有文献详细介绍助力的控制算法。因此，本研究主要针对电动制动助力器的工作原理以及永磁同步电机的矢量控制算法进行控制策略进行深入研究，搭建三闭环矢量控制算法模型，并通过仿真验证了模型的正确性和有效性。

2. 电动制动助力器及控制算法

2.1. 电动制动助力器工作机理

当驾驶员踩下制动踏板时，踏板位移传感器采集驾驶员制动意图并将电信号传递给控制器，控制器接受信号并做相应的分析处理，输出驱动电机的三相PWM信号，助力电机响应控制器的驱动信号开始旋转，经过传动机构减速增扭后直接推动主缸活塞使主缸内建立高压环境，之后在高压制动液推动轮缸活塞，夹紧制动钳，安装在制动钳上的制动块压紧制动盘，完成制动。

2.2. 制动电机控制算法

电动制动助力器内助力电机的类型通常为无刷直流电机(Brushless Direct Current Motor, BLDC)或者永磁同步电机。从结构形式上，PMSM属于BLDC，二者均以永磁体作为转子，没有电刷和换向器，主要区别在于定子的绕组绕线方式不同以及驱动的波形不同，PMSM的反电动势波形为正弦波，BLDC的反电动势波形为梯形波。表1为PMSM和BLDC电机的主要区别。由于BLDC结构的限制，正弦波驱动的效果在PMSM电机上会较好一些。同时，PMSM电机采用的是FOC控制策略，在动态响应上也存在优势。

Table 1. The main differences between BLDC and PMSM

表1. BLDC与PMSM的主要区别

在六步换向法中，定子磁场扭矩只有六个方向，转子在60˚范围内受力方向始终不变，造成定子磁场形成的扭力和转子力臂的夹角不能维持在90˚，如图1所示，这样导致转矩大小也没有得到精确控制，这样的方法不利于提高电机效率及动态响应。电动制动助力器内的电机需要较高的动态响应以保证压力的精确控制，故此方法不适合于控制电动制动助力器内的助力电机。

三相电机内各变量相互耦合，需要一种能够“去耦”的方法以简化三相电机的控制。磁场定向控制可以通过坐标变换(Clark变换、Park变换及其反变换)对定子电流转矩分量和励磁分量进行解耦，使定子磁场形成的扭力始终与转子力臂轴相垂直，保持推力与转子力臂垂直的方向一致，如图2所示。因此可将矢量控制算法来控制助力电机提高相应效率。

3. 电机矢量控制策略

3.1. 矢量控制算法

某车型的控制系统针对电机的矢量控制策略如图3所示，控制逻辑为该电机矢量控制策略的基本框图。

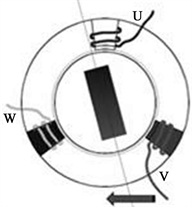(a) 60˚受力 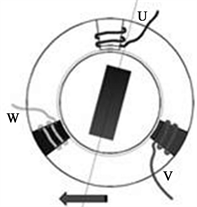(b) 90˚受力

Figure 1. Six-step commutation method rotor force

图1. 六步换向法转子受力

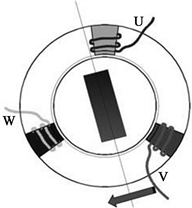(a) −120˚ (b) 120˚

Figure 2. Different angle FOC controls rotor force

图2. 不同角度FOC控制转子受力

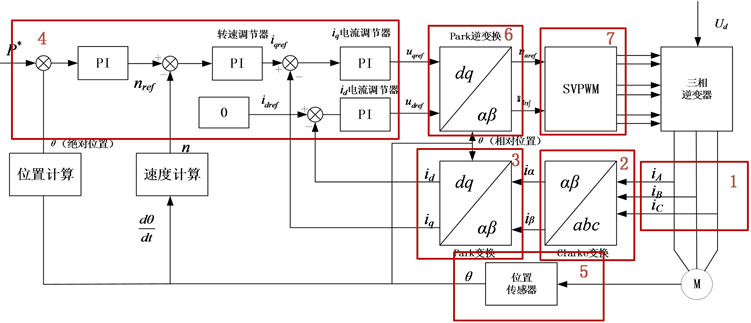
Figure 3. Basic block diagram of vector control

图3. 矢量控制基本框图

如上图，矢量控制过程的步骤如下：

1) 首先测量三相定子电流 $i_A、i_B、i_C$，由于在控制系统中 $i_A+i_B+i_C=0$，因此可以测量任两相的电流就可得到剩下一项的电流。

2) 测得三相电流后将三相电流经过Clarke变换得到具有变量 $i_{\alpha }、i_{\beta }$ 的两轴系统。从定子角度来看， $i_{\alpha }、i_{\beta }$ 是相互正交的时变电流值。

3) $i_{\alpha }、i_{\beta }$ 又经Park变换得到 $i_q、i_d$， $i_q、i_d$ 为变换到旋转坐标系下的正交电流。在稳态条件下， $i_q、i_d$ 是常量。

4) 误差信号由 $i_q、i_d$ 的实际值和各自的参考值(目标值) $i_q^{*}、i_d^{*}$ 进行比较而获得： $i_d$ 的参考值控制转子磁通； $i_q$ 的参考值控制电机的转矩；误差信号是PI控制器的输入；控制器的输出为 $v_q、v_d$，即要施加到电机上的电压矢量，一般FOC算法的控制器采用经典的PI线性控制器，这样可以使系统具有良好的线性特性。

5) 由旋转变压器获得转子位置信息，新的位置信息可告知FOC算法下一个电压矢量在何处，并且位置信息为位置环和转速环提供计算参数。

6) 通过使用新的角度，可将PI控制器的 $v_q、v_d$ 输出值逆变到静止参考坐标系。该计算将产生下一个正交电压值 $v_{\alpha }、v_{\beta }$。

7) $v_{\alpha }、v_{\beta }$ 值经过SVPWM算法得到驱动逆变器的PWM信号，经过逆变器处理最终输出到三相电驱动电机。

由上面的分析，可以得到，FOC的核心在于坐标变换以及SVPWM算法的实现。

3.2. 坐标变换与数学建模

在进行矢量控制时，需要对电机的三相电流进行采样，先进行Clarke变换，获得两相正弦波形，再进行Park变换得到，得到线性波形。

Figure 4. Motor coordinate system

图4. 电机坐标系

如图4，为电机的ABC坐标系、 $\alpha -\beta$ 坐标系， $i_{\alpha }、i_{\beta }$ 分别为电流合成矢量 $i_s$ 在ABC坐标系上的投影。在ABC坐标系下 $i_s$ 可以由式1表示：

$\{\begin{array}{l}{i}_a=i_s\cos \omega t\hfill \\ i_b=i_s\cos \left(\omega t-\frac{2}{3}\text{π}\right)\hfill \\ i_c=i_s\cos \left(\omega t+\frac{2}{3}\text{π}\right)\hfill \end{array}$ (1)

将三相电流投影到 $\alpha -\beta$ 坐标系下，即为Clarke变换 $\left(i_A+i_B+i_C=0\right)$ ：

$\begin{array}{c}{i}_{\alpha }=\frac{3}{2}{i}_a\\ i_{\beta }=\frac{\sqrt{3}}{2}{i}_a+\sqrt{3}{i}_b\end{array}$ (2)

为了保证变换后的矢量和变换前的矢量幅值相等需要乘上一个系数 $m=\frac{2}{3}$ (若为等功率变换则 $m=\sqrt{\frac{2}{3}}$ )。

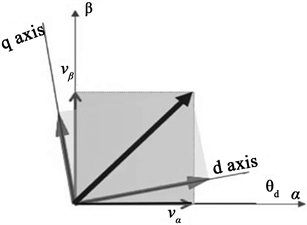
Figure 5. Diagram of Park transformation

图5. Park变换示意图

如图5所示，直角坐标系旋转θ角后，新旧坐标变换公式如下(Park变换)：

$\{\begin{array}{l}{i}_d=i_{\alpha }\cos {\theta }_d+i_{\beta }\sin {\theta }_d\hfill \\ i_q=i_{\beta }\cos {\theta }_d-i_{\alpha }\sin {\theta }_d\hfill \end{array}$ (3)

同理反Park变换为：

$\{\begin{array}{l}{i}_{\alpha }=i_d\cos {\theta }_d-i_q\sin {\theta }_d\hfill \\ i_{\beta }=i_q\cos {\theta }_d+i_d\sin {\theta }_d\hfill \end{array}$ (4)

3.3. SVPWM控制策略

空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)，本质上是对PMSM电机中的三相电压源逆变器功率器件的一种特殊的开关触发顺序和脉宽大小的组合，这种开关触发顺序和组合将在定子线圈中产生三相互差120˚电角度、失真较小的正弦波电流波形。SVPWM相对于其他的方法来说具有消除谐波效果好，便于微控制器实时控制等优点。

为了更好的理解SVPWM，将电机的三相绕组(输出作用端)和6个输出的MOS管(输出端)结合在一起分析，如图6所示，将A+和A−组合起来定义为一组开关S_a，同理可将B+、B−和C+、C−分别组合起来定义成S_b、S_c。可定义一个开关函数：

$S_{x}x=a,b,c\{\begin{array}{l}1上桥臂导通\hfill \\ 0下桥臂导通\hfill \end{array}$ (5)

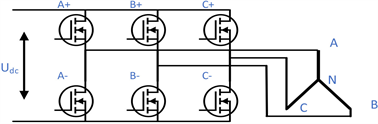
Figure 6. Schematic diagram of three-phase inverter

图6. 三相逆变器示意图

因此总共有8种开关状态，可以得到开关状态与相电压和线电压的对应关系(见表2)。

Table 2. Correspondence between phase voltage and line voltage

表2. 相电压和线电压的对应

其中U₀、U₇为0矢量，主要作用是使目标矢量不失真。由表2，可以做出电压空间矢量图(图7)，由该扇区可以判定电机的有效工作区域。

Figure 7. Sector division

图7. 扇区的划分

3.4. 助力电机控制策略仿真与验证

基于以上矢量控制策略分析，结合电动制动助力器的实际应用需求，如图8所示，在MATLAB/Simulink中搭建了矢量控制策略的仿真模型。将位置、速度、扭矩作为目标输入，模型包括了电机矢量控制的三个闭环，从里到外分别为电流环，速度环及位置环。每个环路的控制都是采用的PI控制器。由式3可以看出d轴电压不仅受到d轴电流的影响，还受到q轴电流的影响，因此d轴电压和q轴电压之间存在耦合关系，相互影响。因此，在电流环的控制中，d轴电压和q轴电压无法实现单独控制，这会影响到电机控制器的性能。在本模型中是通过前馈补偿的方法将耦合项抵消来实现解耦。

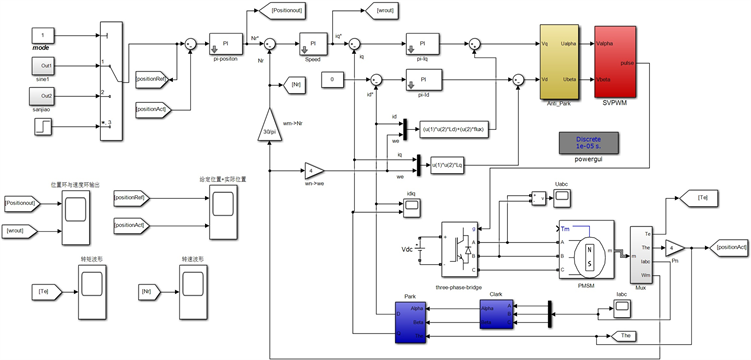
Figure 8. Vector control algorithm model

图8. 矢量控制算法模型

对于电动制动助力器的实际应用来说，三闭环不可缺。电机电流和电机电磁转矩的关系可由式6表示，式中 $p_n$ 为电极对数， ${\psi }_f$ 为转子磁链都是常数，因此，电磁转矩与定子交轴电流呈正比例关系。由上述分析可以得到，控制电机的电流可控制电机的转矩。

$T_e=\frac{3}{2}{p}_n{i}_q{\psi }_f$ (6)

当助力器进行主动建压时，需要在极短时间内达到目标压力，这就要求其助力电机具有快速的响应及跟随目标值的能力。电机控制的速度环可以解决上述问题。电动制动助力器在实际工作中，助力电机不是一直旋转，而是根据控制器的指令而转动到指定位置就停止旋转。此时，助力电机是伺服电机的角色。因此，助力电机的位置环控制是使电机到达指定位置对应着制动系统的不同压力，而速度环是电机输出轴到达目标位置的速度的控制，电流环则是电机输出轴扭矩的控制。

3.4.1. 电流环仿真与验证

如图9所示，在电机启动后0.5 s对模型施加2 N.m的力矩，三相定子电流 $i_A、i_B、i_C$ 呈标准的正弦波变化，经过Clarke变换后将坐标系转变为固定的直角坐标系，得到 $i_{\alpha }$ 和 $i_{\beta }$ (图10)。再经过Park变换将坐标系转变为随转子旋转的坐标系，得到定子扭矩波形电流 $i_q、i_d$。

Figure 9. Three-phase current waveform

图9. 三相电流波形

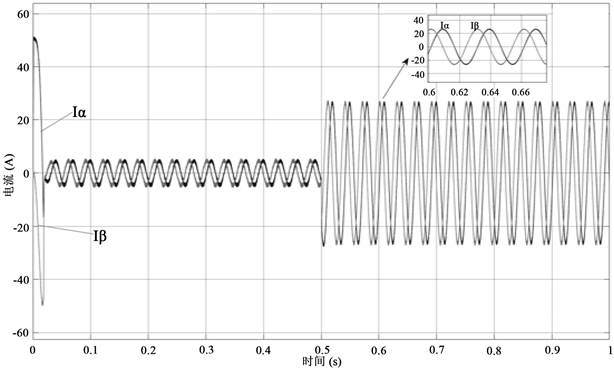
Figure 10. Current waveform after Clark transformation

图10. Clark变换后电流波形

如图11所示，电机启动时有一定的电流波动l d，约为50 A，持续时间0.01秒左右，对电机影响小。当没有负载时扭矩为0，加上负载后电机迅速响应l q，准确度达到99%。

3.4.2. 速度环仿真与验证

如图12所示，给定的转速为500 rpm，电机启动时迅速跟随给定转速，加上负载后速度有20 rpm微小波动，持续0.02秒时间，波动幅度率约为4%，人体感觉不出，波动跳跃后检测出后马上回归稳定继续跟随给定转速。

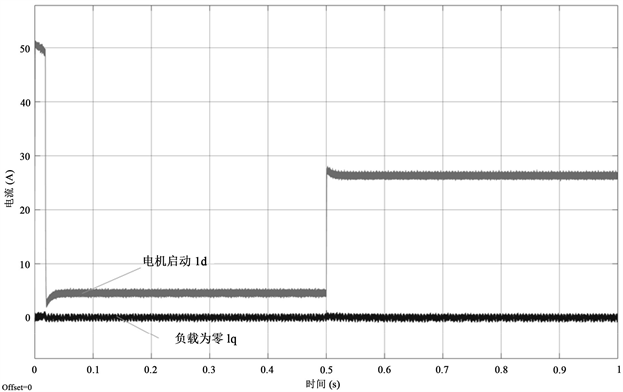
Figure 11. Current waveform after Park transformation

图11. Park变换后电流波形

Figure 12. Speed waveform

图12. 转速波形

3.4.3. 位置环仿真与验证

在仿真模型下，分别给定阶跃、正弦波信号，实际位置和目标位置相对比，目标线型和实际线型基本重合，模型仿真结果如图13和图14所示。

从图中可以看出，正弦连续信号下系统的位置输出能够时刻保持对给定信号的跟随，而阶跃信号下有平滑的滞过渡，持续时间0.02秒左右，幅值微小为0.01 A，准确度约为99%。总体上说，系统跟随性能和快速性能均较为优良。

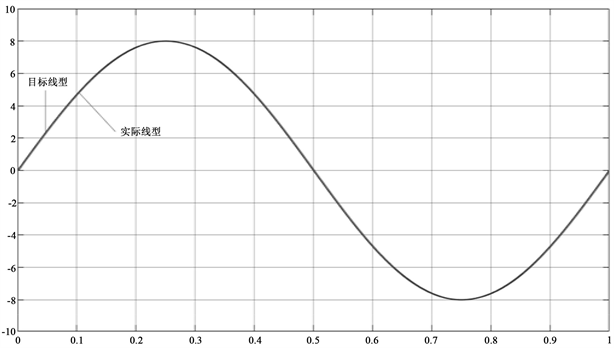
Figure 13. Position following waveform under the sinusoidal signal input

图13. 正弦信号输入下的位置跟随波形

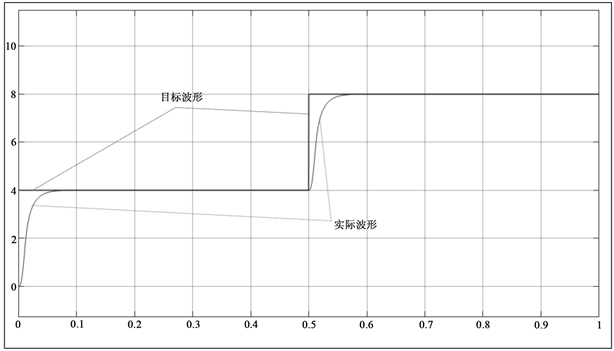
Figure 14. Position following waveform under step signal input

图14. 阶跃信号输入下的位置跟随波形

4. 结束语

通过对比BLDC和PMSM在结构和控制算法上的差异，并对其进行深入研究，主要有以下三个方面的结论：

1) 研究了矢量控制算法来控制助力电机矢量控制的相关策略，并从理论计算和坐标变换的推导，论证了控制策略的合理性和正确性。

2) 提出了电机助力空间矢量脉宽调制的控制策略，通过对相电压和线电压的三相互差120˚角度对比和分析，说明SVPWM具有谐波消除效果好和便于微控制的优点，适合解决系统控制和信号失真的问题。

3) 以MATLAB/Simulink搭建了三闭环矢量控制算法模型，并结合电动制动助力器的运行工况进行了仿真验证，从电流环、速度环和位置环三个维度的仿真精度分别为99%，96%和99%，充分验证了模型的准确性。

致谢

感谢上汽通用五菱汽车股份有限公司项目组领导的大力支持，感谢项目组成员为该项目的开展付出的大量工作。

基金项目

本论文得到“广西特聘专家”专项经费资助，广西创新驱动重大专项(编号：桂科AA19182003)和广西高校中青年教师科研基础能力提升项目(2022KY1412)的支持。

NOTES

^*通讯作者。