基于PSO-SVM的风电整流器故障诊断

Fault Diagnosis of Wind Power Rectifier Based on PSO-SVM

摘要: 针对风力发电系统中整流器故障诊断的问题，以三相全控整流电路为例，提出粒子群优化支持向量机(particle swarm optimization-support vector machine, PSO-SVM)的分类算法。首先用MATLAB进行仿真得到故障信号，再使用快速傅立叶变换(FFT)预处理故障信号，主成分分析(PCA)提取其中主要频域特征，以及采集一周期内的时域特征，最后使用SVM和PSO-SVM分别对提取的时域、频域以及结合时频域的特征进行训练和测试。实验结果表明，采用PSO-SVM的方法对时域、频域、时频域特征的故障诊断率都比SVM要高，诊断时间也得到了大大提升，并且选用时频域特征进行故障诊断要比单独用时域或者频域特征的效果要好。

Abstract: Aiming at the problem of rectifier fault diagnosis in wind power generation system, a classification algorithm based on particle swarm optimization-support vector machine (PSO-SVM) is proposed by taking a three-phase fully controlled rectifier circuit as an example. Firstly, the fault signal is obtained by MATLAB simulation, and then the fast fourier transform (FFT) is used to preprocess the fault signal. The principal component analysis (PCA) is used to extract the main frequency domain features, and the time domain features in a cycle are collected. Finally, SVM and PSO-SVM are used to train and test the extracted time domain, frequency domain and combined time-frequency domain features. The experimental results show that the fault diagnosis rate of time-domain, frequency-domain and time-frequency-domain features using the PSO-SVM method is higher than that of SVM, and the diagnosis time is also greatly improved. The effect of fault diagnosis using time-frequency-domain features is better than that using time-domain or frequency-domain features alone.

1. 引言

风电能源作为可再生能源在世界能源中的地位越来越重要 [1] [2]。风电机组通常工作在戈壁滩、大草原、海面上等较恶劣的环境中，受交变载荷和环境因素影响较大，因此故障率更高，故障发生后多采用事后停机维修的方式以恢复系统运行，风力发电机组系统运行成本得到极大地提高，经济效益降低了。再加上风力发电系统本身是一个非线性、多变量、强耦合的系统，当参数出现不确定时，系统的控制将会更加复杂极易发生故障 [3]。因此对风力发电系统进行实时故障诊断很有必要。典型的永磁直驱风力发电系统如图1所示，包括风力机、永磁同步电机、整流器、逆变器和控制系统。

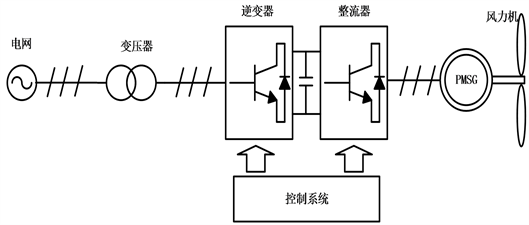
Figure 1. Permanent magnet direct-drive wind power system

图1. 永磁直驱风力发电系统

随着风力发电技术的发展，风力发电系统的故障诊断技术也已经逐步发展起来，学者和专家们提出了众多的故障诊断方法。对于风力发电控制系统，文献 [4] 针对系统潜在的执行器部分失效故障、未知扰动偏差故障等不确定问题，提出一种MPPT滑模主动容错控制方法。通过滑模观测器(SMO)重构实际系统的执行器故障，并将故障观测估计项引入MPPT容错控制律。采用高阶滑模控制(SMC)设计MPPT容错控制器，形成风力发电系统在线故障诊断和容错控制的集成。文献 [5] 提出基于小波包分析的逆变器故障检测方法。用小波包对在开关元件IGBT各类开路故障状态下逆变器的输出电压信号进行分解，采用功率谱方法分析小波包分解后输出电压信号的细节，最后通过频谱特征和功率谱识别出逆变器的各类故障。文献 [6] 永磁同步风电系统变流器故障，提出振动信号用于变流器故障诊断的可行性，论证电流与发电机结构动态响应之间的关联机制和基于振动信号的故障诊断定位规律。

整流电路在风电设备中也是不可或缺的一部分，并且广泛应用于工业领域、交通运输、电力系统及其他领域，具有大功率、可平衡电网、易完成能量转移等优点。整流电路中的开关器件具有开关频率高，开关损耗大的特点，器件容易因为散热不及时而造成损坏，不仅会增大整流电压纹波，而且会使负载工作在不正常状态。另外，器件损坏时间短，通常在几微秒，这些特点使得器件发生故障前不容易被观察。这也就要求较高的故障诊断准确率以及较短的故障诊断时间，保证快速准确的获得电路的故障情况 [7]。

本文将整流电路输出的电压信号ud作为故障信号进行处理，提取ud时域、频域特征，在时域、频域以及综合时域和频域的特征三个角度，采用SVM和PSO-SVM故障诊断方法比较准确率以及故障诊断时间。同时在SVM和PSO-SVM两种诊断方法的角度观察时域、频域、时频域特征对故障诊断的影响。

2. 故障分析

本文以三相桥式整流 [8] [9] 电路为例，如图2所示，由6只晶闸管组成，VT1、VT3、VT5为共阴极组，VT4、VT6、VT2为共阳极组，晶闸管导通顺序为VT1-VT2-VT3-VT4-VT5-VT6。在电路工作的任意时刻中，都会有两只晶闸管导通形成电流回路，其中每隔π/3换相一次，而换相过程总是在共阴极和共阳极组间轮流进行。ud比较容易测量，并能反映电路的运行状况，因此本文将ud作为主要的分析对象。

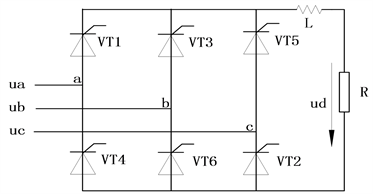
Figure 2. Three-phase bridge rectifier circuit

图2. 三相桥式整流电路

三相桥式整流电路故障主要表现为晶闸管的开路和短路故障，而对于晶闸管的短路故障，在三相桥的每一桥臂装短路保护作用的熔断器时，晶闸管短路故障也相当于开路故障。因此本文主要考虑晶闸管的开路故障，对于在实际运行中发生最多的单只晶闸管和两只晶闸管发生开路故障，主要有以下几种类别。

类别1，无晶闸管故障，即正常工作。

类别2：只有一个晶闸管故障，即 VT1、VT2、VT3、VT4、VT5、VT6中有一个故障。

类别3：同一桥臂上的两个晶闸管同时故障，即VT1和VT4、VT2和VT5、VT3和VT6两个同时故障。

类别4：共阴极的两个晶闸管或共阳极的两个晶闸管同时故障，即VT1和VT5、VT3 和VT5、VT1和VT3、VT2和VT4、VT4和VT6、VT2和VT6。

类别5：共阴极的一个晶闸管和共阳极的一个晶闸管同时故障，即VT1和VT2、VT1和VT6、VT2和VT3、VT3和VT4、VT4和VT5、VT5和VT6。

本文选择类别5中较为困难的6类故障来进行故障诊断分析，如表1所示。

Table 1. Classification of thyristor open-circuit faults in three-phase rectifier circuit

表1. 三相整流电路的晶闸管开路故障分类

3. 故障特征提取

3.1. 时域特征提取

按照表1三相整流电路晶闸管开路故障分类情况在MATLAB中建立仿真模型，取三相电压u = 380 V，f = 50 Hz，R = 2 Ω。两种典型故障情况下整流电路输出电压如图3和图4所示，ud波形表现为只是在时间轴上的平移。

因此选取第一个完整周期内电压达到峰值时所对应的3个时间点为特征信息，分别记为X1、X2、X3。得到时域144 × 3样本特征矩阵，部分特征数据如表2所示。

在时域上，本文以整流电路输出电压ud构建原始诊断数据样本，包括6种故障状态，采样频率为10 kHz，采样时间为1 s，每组样本数据9902个点，每种故障类别采集触发角α为0˚、30˚、60˚和90˚时的4组数据，共采集24组诊断数据。对采集的24组诊断数据混入高斯白噪声破坏5次，每一次得到新的24组诊断数据。以最初的24组数据和高斯白噪声破坏后的数据作为原始诊断数据，即原始9902 × 144样本矩阵。

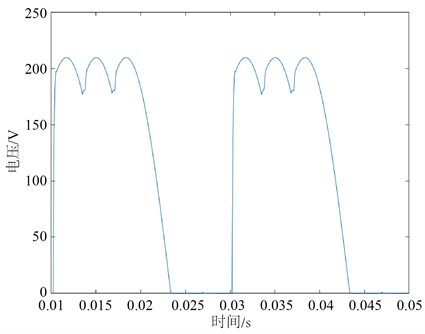
Figure 3. VT1 and VT6 open-circuit rectifier circuit outputs

图3. VT1和VT6开路整流电路输出

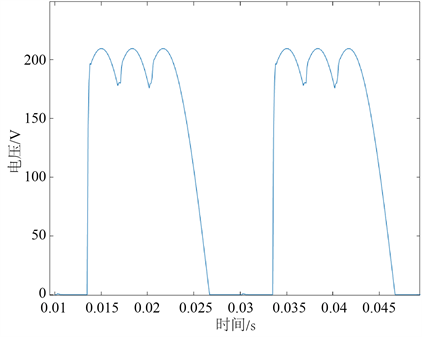
Figure 4. VT1 and VT6 open-circuit rectifier circuit outputs

图4. VT1和VT2开路整流电路输出

Table 2. Time domain feature extraction

表2. 时域特征提取

3.2. 频域特征提取

触发角α为0˚时6类故障的局部频谱图如图5所示，在发生不同故障时同一频率下的幅值有明显的区别，因此选择输出电压ud的频谱为研究对象进行频域的特征提取。

采用FFT技术处理离散的输出电压信号，实现对原始数据时域到频域的变换，采用PCA对FFT后的数据进行降维处理。PCA可以降低输入数据空间的大小，减少训练和测试时间，还可以减少噪声干扰，提高映射性能，这样可以达到改善诊断能力的目的。

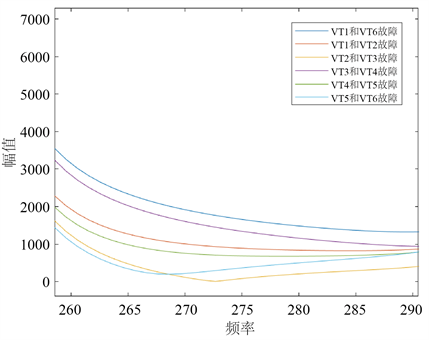
Figure 5. The local spectrum of six kinds of faults

图5. 6类故障的局部频谱图

1) 快速傅里叶变换 [10] (FFT)

采样得到一个离散输出的电压信号 ${\left\{f_n\right\}}_0^{N-1}$，运用式(1)和式(2)进行FFT变换。

$F_k=G_k+W_N^k{H}_k$ (1)

$F_k=G_k+W_N^k{H}_k$ (2)

其中 $W_N=e^{-j2\text{π}/N}$ ；N = 采样点数； $k=0,\cdots ,N/2-1$ ；G_k是f_n的偶数序列的求和，H_k是f_n数序列的求和；G_k和H_k可以通过式(3)、式(4)计算。

$G_k={\displaystyle \underset{n=0}{\overset{\left(N/2\right)-1}{\sum }}{f}_{2n}{W}_{N/2}^{nk}}$ (3)

$H_k={\displaystyle \underset{n=0}{\overset{\left(N/2-1\right)}{\sum }}{f}_{2n+1}{W}_{N/2}^{nk}}$ (4)

2) 主成分分析法 [11] (PCA)

采用主成分分析法将通过FFT获得的频域特征向量进行降维处理，同时相对保留原有波形的重要特征，主要步骤如下：

设故障信号采样点数为r个，则经过FFT后的一个故障波形数据谐波向量可以表示 $x={\left(s_1,s_2,\cdots ,s_r\right)}^{\text{T}}$，其中S_n表示第n个采样点的FFT结果。

① 设故障信号经过FFT变换后的谐波总数为N，则样本空间为(X₁X₂…X_N)，再根据式(5)求取全体样本的平均值向量m；

② 根据全体样本的平均值m，计算样本的协方差C_x，如式(6)所示；

③ 选取样本的协方差矩阵前l大的特征值和所对应的特征向量构成转换矩阵A，如式(7)所示；

④ 将每组故障波形数据向量通过式(8)获得新的降维向量y，实现对原始故障数据的降维处理。

$m=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{x}_i}$ (5)

$C_x=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(x_i-m\right)}^{\text{T}}\left(x_i-m\right)}=X^{\text{T}}X$ (6)

$X=\frac{1}{\sqrt{N}}\left[\left(x_1-m\right),\left(x_2-m\right),\cdots ,\left(x_N-m\right)\right]$

$u_i=\frac{1}{\sqrt{N}}X{v}_{i}i=1,2,\cdots ,l$ (7)

$A=\left(u_i,u_2,\cdots ,u_l\right)$

$y_i=A^{\text{T}}{x}_{i}i=1,2,\cdots ,N$ (8)

经过FFT对原始信号进行频谱分析，得到144组多维的故障特征量，各分量间相互关联，且信息存在冗余，不便于故障分类。采用PCA故障特征提取算法对已经提取的故障特征向量来进行降维处理。主元分析的帕累托图，如图6所示。

从图5可知，前3个主成分的累计贡献率占主体部分，因此选择144组PCA降维后的前3个主成分作为频域最终的故障特征向量，能够保留了故障特征信号大部分特征信息，同时维度得到了降低，训练和测试时间也得到减少。

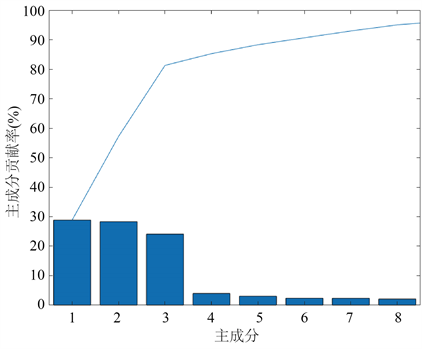
Figure 6. Pareto diagram of principal component analysis

图6. 主成分分析法的帕累托图

4. 故障诊断

4.1. 诊断算法

下面主要介绍本文采用的SVM和PSO-SVM故障诊断方法。图7是故障诊断方法流程图。

1) 支持向量机 [12] (SVM)

支持向量机(SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可用于模式分类和非线性回归，SVM方法是从线性可分情况下的最优分类超平面提出的，对于两类分类问题，假定n个样本的训练集：

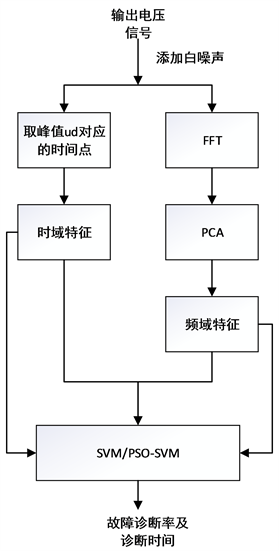
Figure 7. Flow chart of fault diagnosis

图7. 故障诊断流程图

$D=\{\left(x_i,y_i\right)|i=1,2,\cdots ,n\}$ (9)

其中， $x_i\subseteq R^n$， $y_i\subseteq \{+1,-1\}$。

能被一个超平面 $H:w\cdot x+b$ 完全区分开，为了最大化超平面的分类间隔，需要求解下列二次优化问题：

$\underset{w,b}{\min }\frac{1}{2}{\Vert w\Vert }^2=\underset{w,b}{\min }\frac{1}{2}{w}^{\text{T}}w$ (10)

$s.t.y_i\left[w\cdot x_i+b\right]-1\ge 0$ (11)

其中， $i=1,2,\cdots ,n$。其对偶问题是一个凸二次规划优化问题，其解可通过求解拉格朗日函数获得，最终得到决策函数：

$f\left(x\right)=\mathrm{sgn}\left[{\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i{y}_i\left(x_i\cdot x\right)+b}\right]$ (12)

构造这类决策函数的学习机器称为支持向量机。对于非线性的情况，SVM利用一个非线性的映射把原数据集中的向量点转化到一个更高维度的空间中，再在这个空间中构造最优线性分类超平面。

SVM一般形式为：

$\{\begin{array}{l}\underset{w,b,\xi }{\min }\left(\frac{1}{2}{\Vert w\Vert }_2^2+C{\displaystyle \underset{i=1}{\overset{l}{\sum }}{\xi }_i}\right)\\ y_i\left(\left(w,\phi \left(x_i\right)\right)-b\right)\ge 1-{\xi }_i\\ \\ {\xi }_i\ge 0,i=1,2,\cdots ,l\end{array}$ (13)

式中：C为SVM惩罚参数， ${\xi }_i$ 为松弛变量； $x_i$ 为故障特征样本； $y_i$ 为样本标签。核函数采用径向基函数(radial basis function，RBF)可以克服高维特征空间上的内积困难。

$K\left(x_i,x\right)=\exp \{-g{\Vert x-x_i\Vert }^2\}$ (14)

式中： $x_i$ 为故障特征样本输入；g为核参数。

径向基参数g和支持向量机惩罚参数C的取值大小影响样本训练和测试过程，容易导致SVM分类结果陷入局部最优以及过拟合等现象，从而影响SVM模型的故障诊断效果。

2) 粒子群算法(PSO)

粒子群算法的基本思想：通过设计一种只有有速度和位置两个属性的粒子，速度代表移动的快慢和方向，位置代表当前的所处位置。每个粒子都单独的在活动空间中搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置 [13]。

每个粒子都代表一个故障特征训练样本的适应度，初始状态下粒子随机分布在整个D维搜索空间中，第i个粒子的位置标示为 $X_i=\left[x_i{}_1{x}_i{}_2\cdots x_{iD}\right]$，其速度表示为 $v_i{}_1=[v_i{}_1{v}_i{}_2\cdots v_{iD}]$ $i=1,2,\cdots ,N$。粒子的速度和位置状态更新如式(15)所示。

$\{\begin{array}{l}{v}_{id}^k=\omega v_{id}^{k-1}+c_1{r}_1\left(P_{id}-x_{id}^{k-1}\right)+c_2{r}_2\left(P_d-x_{id}^{k-1}\right)\\ x_{id}^k=x_{id}^{k-1}+v_{id}^{k-1}\end{array}$ (15)

式中： $v_{id}^k$， $x_{id}^k$ 分别为粒子i第k次迭代后第d维上的速度矢量和位置矢量； 为线性递减的惯性权重，能够逐步提高局部搜索能力；c₁、c₂为加速度常数，调节学习步长；r₁、r₂为相互独立的[0, 1]上的随机数；本文选择故障诊断准确率为适应度函数f(x)，则P_id为第i个粒子个体到目前位置搜索到的最佳适应度位置；P_d为整体群体到目前位置搜索到的最佳适应度位置，由此计算径向基参数g和支持向量机惩罚参数C的值，用式(16)更新。

$\{\begin{array}{l}{P}_{id}^k=\{\begin{array}{l}{P}_{id}^{k-1},f\left(x_{id}^k\right)\ge f\left(P_{id}^{k-1}\right)\\ x_{id}^k,f\left(x_{id}^k\right)<f\left(P_{id}^{k-1}\right)\end{array}\\ P_d=P_{id}|\min \{f\left(P_{id}\right)\},i=1,2,\cdots ,N\end{array}$ (16)

粒子群算法优化SVM的流程图如图8所示。

4.2. 诊断分析

分别将144组时域、频域和时频域故障特征向量以8:2的比例随机划分为训练集和测试集，即115组训练集，29组测试集。

小波分析是一种常用的时-频分析方法，小波包分解弥补了小波分析没有在细节成分上进行分解和提取的缺陷。本文对原始信号进行4层小波包分解，对能量最高的频段进行功率谱分析，根据频谱图和相应谱值建立故障特征的数据样本。同一故障的特征在不同的触发角α下区别较大，极大影响了故障诊断结果，因此选择α = 0˚时的36组数据进行小波包时频特征的提取。

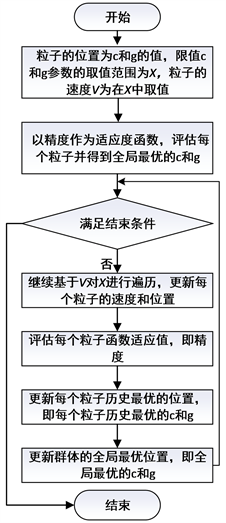
Figure 8. SVM Flow Chart of Particle Swarm Optimization

图8. 粒子群算法优化SVM流程图

通过SVM和PSO-SVM算法进行故障诊断，计算5次平均故障诊断准确率作为最终的诊断准确率。训练模型准确率、测试模型准确率和诊断时间如表3所示。

Table 3. Diagnosis results

表3. 故障诊断结果

分析表3可知，在同一个特征类型下，无论是单次的还是平均的训练模型准确率、测试模型准确率以及诊断时间，PSO-SVM都要好于SVM。说明PSO-SVM诊断模型能够较好的识别和辨别故障特征，同时有很好的抗噪声的能力，在实际的电路中能得到更好的应用。

在同一个故障诊断模型下，提取不同的特征对诊断结果也有很大的影响，在本文故障诊断的背景下，采样时频域特征的准确率要高于采用时域和频域特征的准确率。说明综合了时域和频域的特征提取，能够更加全面的掌握故障特征，在一定程度上可以提高故障诊断的准确率，比常用的小波包时频分析方法有更好的效果。但同时也会增加故障特征的复杂度，增加故障诊断的时间。

5. 结论

本文针对三相桥式整流电路，以输出电压ud作为原始故障信号，采用SVM和PSO-SVM两种故障诊断方法对晶闸管故障进行开路故障诊断分析。从时域、频域和时频域三个方面对原始故障信号提取故障特征，作为SVM和PSO-SVM故障诊断模型的输入。实验结果表明，PSO-SVM相比于SVM能够更好的对故障进行识别、诊断以及抵抗噪声的能力，此外综合时频域特征虽然增加了故障特征的复杂度，但较于常用的小波包时频分析方法效果更好，可以适当提高故障诊断的准确率，在实际的电路中能得到更好的应用。