基于POI数据的住宅价格空间分异特征及影响因素研究——以成都市为例

A Study on the Characteristics and Influencing Factors of Housing Price Spatial Differentiation Based on POI Data—A Case Study of Chengdu City

摘要: 住宅价格因资源配置的不均衡呈现空间异质性，理解住宅价格空间分异特征及其影响因素将为实现土地优化配置和房地产市场调控提供理论依据。在此背景下，该文基于POI数据，采用空间效应检验、Kriging插值法和地理加权回归模型等方法对研究区域的住宅价格空间分异特征及影响因素进行分析。结果显示：① 成都房价的空间分布在大部分地域呈现圈层结构形态，在金堂县以及简阳市呈现多核心分布形态。② 在成都市住宅市场房价的影响因素中，邻里因素的影响程度最大，然后是区位因素，最后才是结构因素。③ 成都市居民住房需求已由“生活便利型”转为“生活质量型”，对改善型住房的需求日益增长。

Abstract: The housing price presents spatial heterogeneity due to the imbalance of resource allocation. Understanding the characteristics and influencing factors of the spatial differentiation of housing price will provide a theoretical basis for the realization of optimal land allocation and real estate market regulation. In this context, based on POI data, this paper uses spatial effect test, Kriging interpolation method and Geographic regression weighted model to analyze the characteristics and influencing factors of housing price spatial differentiation in the study area. The results show that: 1) The spatial distribution of housing price in Chengdu presents a circular structure in most regions, and a multi-core distribution pattern in Jintang County and Jianyang City. 2) Among the influencing factors of housing price in Chengdu, neighborhood factor is the most influential, followed by location factor, and finally is structural factor. 3) The housing demand of Chengdu residents has changed from “convenience” to “quality of life”, and the demand for improved housing is increasing day by day. 

1. 引言

住房问题一直是学术界和社会的研究热点问题，因住房的保值特性和价值特征使得该问题的研究呈现多学科交叉的态势。房价上涨究其根本原因是市场供需不平衡，又因资源配置的不均衡性呈现空间异质性 [1] ，且在社会制度、自然条件、经济条件等多因素影响下，房价通常会在区域空间上表现出较为明显的分异特征 [2] 。近十年来，成都市住宅价格已上涨137%，然而现目前对成都房价的相关研究仍大多停留在数量关系上，缺乏对房价空间属性的思考。

2. 文献综述

国外早期的区位论和地价地租理论为房价的研究奠定了理论基础 [3] ，而随着特征价格模型和消费者理论的引入，使得房价影响因素的定量研究得到快速发展，如李颖丽等人以重庆市主城区小区均价数据为基础，采用特征价格模型，探究了多中心山地城市住房价格影响因子空间异质性的最佳方法 [4] ；唐钱龙等人通过构建特征价格模型，以房价作为被解释变量，探究了长沙市轨道交通对沿线住宅价格的影响 [5] ；黄醇醇等人运用特征价格模型分析了城市轨道交通新建线路对沿线住宅价格增值的时空效应 [6] 。

伴随着空间计量经济学的发展，有学者将GWR模型引入到房价及其影响因素的研究领域中 [7] ，逐步解释了公交站、地铁站、CBD等要素对房价的影响过程、作用方式和形成机理 [8] 。GWR模型由于在处理诸如房价等空间数据时能更好的处理空间异质性问题，目前正广泛应用在房价及其影响因素的研究领域中，如吴启睿等人运用GWR模型，结合Kriging插值法，探究了广州市住宅价格空间分布结构及其影响因素 [9] ；胡炜等人运用GWR模型，量化影响因素对住宅地价作用的空间分异规律，确定影响因素单位变化对应的地价修正百分比 [10] ；陈子轩等人利用空间插值方法分析北京二手房住宅价格空间格局，采用地理加权回归模型分析住宅价格空间分布影响因素 [11] 。且有学者从空间演变角度出发，认为各地住宅存在一定的空间分异规律，尹上岗等人运用GIS地统计分析中的普通Kriging插值法对“一主三副”住宅价格空间分布进行模拟和估计，认为南京住宅价格空间结构为同心圆和扇形融合的混合模型 [12] 。从模型优化上这一角度，已有诸多研究表明GWR的模型解释力度要优于特征价格理论、一般线性回归模型 [13] 以及空间拓展模型 [14] 。

综上所述，已有研究对住宅价格的空间分异已做出了较多探索，但仍有不足，主要可归结为以下几点：第一，目前研究多集中于北上广深等一线城市，缺乏对成都、重庆等新一线城市住宅价格空间分异特征及其影响因素的研究；第二，在数据使用上多采用单一的截面数据，对空间数据的使用较少。POI，也被称为兴趣点，泛指电子地图中包含名称、地址、坐标和类别等信息的点数据。鉴于此，本文将基于POI数据，运用空间效应分析、Kriging插值和地理加权回归模型，以成都市住宅价格为研究对象，研究其空间分异特征与影响因素，为建立房价动态检测体系提供技术借鉴，为实现土地优化配置和房地产市场调控提供理论依据。

3. 研究方法

3.1. 空间效应检验

国内已有许多学者认为住宅价格受区位因素的影响 [15] ，其价格呈现一定的空间变化趋势。空间效应包括空间相关性和空间异质性。在进行GWR模型建立之前，需对样本进行空间相关性检验，本文将采用Moran's I进行空间相关性的检验。其计算公式为：

$I=\frac{n}{S_0}\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{ij}\left(x_i-\bar{x}\right)\left(x_j-\bar{x}\right)}}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\left(x_i-\bar{x}\right)}^2}}}$ (1)

在表达式中：n代表样本楼盘总数； $w_{ij}$ 为两个属性之间的空间权重； $x_i$ 和 $x_j$ 为第i个楼盘和第j个楼盘的属性值； $\bar{x}$ 为均值； $S_0={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_{ij}}}$ 。

相较于全局空间自相关，局部空间自相关则是计算分析区域内各个空间对象与其邻域对象间的空间相关程度，计算分析空间对象分布中所存在的局部特征差异，反映局部区域内的空间异质性与不稳定性。本文将采用Anselin(也被称为Lisa)进行局部空间自相关分析。

3.2. Kriging空间插值

在已收集到的POI数据满足具有空间相关性的前提和考虑空间数据的位置与相关性的基础上，利用半方差函数对观测半径范围内观测点的权系数进行估计，相较于IDW (反距离权重插值法)插值法而言，Kriging空间插值法在处理较多数据样本时具有可信度高，误差小的优点，其表达公式为：

$Z\left(S_0\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\lambda }_i}Z\left(S_i\right)$ (2)

其中n为研究区域内住宅样点个数；S_i为住宅样点i的空间位置，Z (S_i)为该位置样点i的住宅价格；Z (S₀)为未知点S₀处住宅价格的估计值； ${\lambda }_i$ 为待求权系数。

3.3. 地理加权回归模型

在构建地理加权回归模型之前，需要通过建立一个较为合理的OLS模型，为GWR模型的建立构建框架基础 [16] 。GWR模型基于非参数局部加权回归技术，能更好的处理空间数据之间的空间依赖性和空间异质性问题，其表达公式为：

$y_i={\beta }_0\left(u_i,v_i\right)+{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\beta }_k}\left(u_i,v_i\right)x_{ik}+{\epsilon }_i$ (3)

其中 $y_i$ 为第i个观测点单位面积房价； $x_{ik}$ 是第i观察点处第k项解释变量的值； $u_i$ 和 $v_i$ 分别是该地经度和纬度； ${\beta }_0\left(u_i,v_i\right)$ 为常数项； ${\beta }_k\left(u_i,v_i\right)$ 是第i观察点的回归系数值；n为解释变量的数量； ${\epsilon }_i$ 为随机误差。

4. 变量选取与模型建立

4.1. 研究区域概况与数据来源

成都市(占地面积14,335平方公里)是四川省的省会城市，国家重要的高新技术产业基地、商贸物流中心和综合交通枢纽，蜀文化的发源地，也是我国十大古都之一，距第七次全国人口普查结果显示，成都市人口已达2093.78万人。成都市作为成渝地区双城经济圈的节点城市，其住宅价格的空间分异特征广受关注。

本文选取成都为研究区域，以不同住宅社区为研究单元，用八爪鱼软件的自定义规则在安居客(https://chengdu.anjuke.com/)、房天下(https://cd.fang.com/)和58同城(https://cd.58.com/)等网站上爬取住宅价格以及部分影响因素(卧室个数、建筑面积、楼龄、到地铁站的距离等)数据，以此来构建GWR模型。经过数据预处理，剔除数据明显错误和属性缺失的数据，最终得到2482个取样点。相关的公交站点和地铁站点以及公共设施配套数据等数据来自谷歌地图(http://www.gditu.net/)。

4.2. 变量选取

国内外诸多学者都已从结构因素、邻里因素等方面对房价的空间分异进行了研究，唐文彬等人基于空间计量视角构建地理加权回归模型(GWR)，选取了区位、结构、邻里等三个方面12个变量分析了城市轨道交通(URT)沿线住宅租金的空间分异特征 [17] ；张菲凡等人从内生因素、区位特征、邻里特征3个维度选取9个解释变量，构建GWR模型分析各变量对海甸岛房价的影响效应 [18] ；鲍雅君等人从区位属性、邻里环境以及建筑特征等维度中选取了等9个解释变量对研究区住宅价格及其影响因素、驱动机制进行研究 [19] 。

本文为全面研究空间因素对于住宅价格的影响，基于上述的相关研究，还将房龄、绿化率，房源与最近中小学和医院的距离(采用欧式距离，利用Arc GIS近邻分析得出 [20] )等因素考虑进来，经过SPSS 25初步分析，在结构因素、区位因素和邻里因素三个维度中选择9个解释变量作为房价影响因素，影响因素的详细内容见表1。

由于各个变量之间可能存在相关性，而解释变量间的相关性过高会导致模型的误差较大 [21] ，因此在构建模型之前先采用SPSS 25利用VIF (方差膨胀因子)进行共线性检验，BED、AREA、COST、FAR、METRO、BUS、PARK、HOS和CBD这9个变量均通过共线性检验。

4.3. 半对数形式GWR模型构建

GWR模型是以特征价格模型为基础发展起来的模型，其模型形式跟特征价格模型一样也有线性、半对数和对数三种形式，经已有研究可以发现，在多数情况下，半对数形式有更好的解释力度 [22] [23] 且能够更好的减轻异方差性问题 [24] ，因此本文将选取半对数GWR模型进行研究，其表达公式为：

Table 1. Selection and description of explanatory variables

表1. 解释变量的选取和描述

$\begin{array}{c}\ln y_i={\beta }_0\left(u_i,v_i\right)+{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\beta }_1\left(u_i,v_i\right)x_{ij}\left(\text{BED}\right)}+{\displaystyle \underset{k=2}{\overset{n}{\sum }}{\beta }_2}\left(u_i,v_i\right)x_{ij}\left(\text{AREA}\right)+{\displaystyle \underset{k=3}{\overset{n}{\sum }}{\beta }_3}\left(u_i,v_i\right)x_{ij}\left(\text{COST}\right)\\ +{\displaystyle \underset{k=4}{\overset{n}{\sum }}{\beta }_4}\left(u_i,v_i\right)x_{ij}\left(\text{FAR}\right)+{\displaystyle \underset{k=5}{\overset{n}{\sum }}{\beta }_5}\left(u_i,v_i\right)x_{ij}\left(\text{METRO}\right)+{\displaystyle \underset{k=6}{\overset{n}{\sum }}{\beta }_6}\left(u_i,v_i\right)x_{ij}\left(\text{BUS}\right)\\ +{\displaystyle \underset{k=7}{\overset{n}{\sum }}{\beta }_7}\left(u_i,v_i\right)x_{ij}\left(\text{PARK}\right)+{\displaystyle \underset{k=8}{\overset{n}{\sum }}{\beta }_8}\left(u_i,v_i\right)x_{ij}\left(\text{HOS}\right)+{\displaystyle \underset{k=9}{\overset{n}{\sum }}{\beta }_9}\left(u_i,v_i\right)x_{ij}\left(\text{CBD}\right)\end{array}$ (4)

5. 实证结果分析

5.1. 空间分异特征

将收集到的2482个房价数据利用ArcGIS中Kriging插值法进行空间可视化表达(图1)。

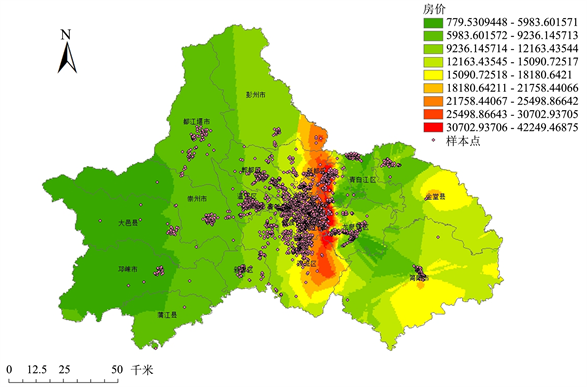
Figure 1. Housing price spatial distribution map of Chengdu

图1. 成都市房价空间分布图

从得到影像中可以看出成都市房价在研究区域大部分地块上明显呈现圈层结构式分布，房价高值区包含了新都区、金牛区、锦江区和双流区，呈现由市中心向郊区降低的分布趋势，从新区划分上来看，高值区多位于天府新区、高新区等地；而在成都主城区西边的彭州市、郫都区、温江区、新津区、邛崃市、大邑县、浦江县等地则处于成都市房价低值区，是成都主城区房价的延伸部分；成都市东部的金堂县和简阳市则呈现多核心分布趋势，房价高值位于其商业发达地带。

利用GeoDa软件对采集的样本数据进行空间效应检验，最终得到莫兰指数(Moran’s I)为0.883 > 0，ρ值为0.0001 < 0.05，说明样本数据具有较强的空间相关性，因此可以构建GWR模型。基于LISA聚类地图可发现，高–高值区位于新都区、金牛区、锦江区和双流区；高–低值区位于龙泉驿区、简阳市和金堂县；低–高值区零星分布在新都区和成化区；低–低值区分布较广，主要位于主城区以外区县。

5.2. 模型结果对比分析

GWR是由特征价格模型(HPM)模型优化而来，因此在构建GWR模型前，首先构建OLS模型，从而可以筛选出对住宅价格解释不够显著的变量，以提高GWR模型的拟合优度。利用SPSS 25软件构建线性回归模型，方法选用步进法。其回归分析结果显示(表2)，在使用半对数模型后，OLS模型调整后R²达到了0.435，大于未取对数住宅价格时的0.362，显然半对数模型具有更好的拟合优度。由表2可知，模型整体显著性水平较高，且根据共线性诊断结果可看出，这九个解释变量之间不存在线性相关关系，因此可以用这九个解释变量构建GWR模型。

Table 2. Statistical table of calculation results of OLS model

表2. OLS模型计算结果统计表

将样本数据导入到GWR 4.0中进行模型结果比较，比较结果如表3所示。GWR模型的AIC值和残差平方和都相对与OLS模型而言有了大幅度的下降，其变化值分别为94.765和131.599。模型的拟合优度由0.435提升为0.697，提升了0.262，从R²、AICc和RSS (残差平方和)三个值的比较来看，GWR在对于住宅价格这样的空间数据上的解释力度是明显强于OLS模型的，这也与现今许多学者的研究结果相符。

Table 3. Comparison table of fitting results between OLS model and GWR model

表3. OLS模型与GWR模型拟合结果比较表

表4中的OLS估计系数和GWR回归系数平均值反映了各个解释变量对研究区域内住宅价格的边际贡献程度。从GWR模型的结果中我们可以看出物业管理费(COST)这个解释变量的回归系数均为正值，表明物业管理费这一解释变量在研究区域内对房价有提升作用且方向在研究区域内保持一致；而卧室个数(BED)、建筑面积(AREA)、容积率(FAR)、到最近地铁站的距离(METRO)、到最近公交站的距离(BUS)、到最近公园的距离(PARK)、到最近三甲医院的距离(HOS)、到最近CBD的距离(CBD)，这几个解释变量回归系数符号有正有负，表明另外八个解释变量在研究区域内对住宅价格的影响存在一定的空间异质性。

Table 4. Geographically weighted regression model estimation results

表4. 地理加权回归模型估计结果

对其各个系数的平均值取绝对值，可以得到各个因素对于房价影响的相对贡献程度，其排序为：到最近三甲医院的距离(HOS) > 到最近CBD的距离(CBD) > 到最近公交站的距离(BUS) > 到最近地铁站的距离(METRO) > 物业管理费(COST) > 到最近公园的距离(PARK) > 建筑面积(AREA) > 容积率(FAR) > 卧室个数(BED)。从这一结果可以得出研究区域内，到最近三甲医院的距离对住宅价格的影响最大，其次是到最近CBD的距离，而诸如建筑面积、容积率和卧室个数的影响程度较小。由此可以看出成都市消费者最为看中的是楼盘的邻里因素，然后是区位因素，最后才是结构因素。

这跟成都的现常住人口多为“蓉漂”有关，成都的虹吸效应不断吸引周边二三线城市的人口前来务工，处于安家的需要，这一代“蓉漂”将优先考虑楼盘的邻里因素，以方便其定居生活，其次会考虑区位因素，以方便通勤，而结构因素对其购房的影响程度相对而言也就较为微弱了。

5.3. 回归系数空间格局分析

5.3.1. 邻里因素

① 到最近三甲医院的距离(HOS)。到最近三甲医院的距离的回归系数取值在−0.576~0.316，均值为−0.196，标准差为0.029，从其影响程度的空间格局中可看出(图2)，在研究区域内的大部分区域其回归系数为负，表明离医院距离越近，对房价提升作用越强。医院本就是为城市居民提供医疗服务的场所，在进行住宅销售时，各类三甲医院会被宣传成为公共配套的一部分，公共配套设施越完善，对房价提升作用也就越强。

Figure 2. Spatial distribution of HOS effects on housing prices

图2. HOS对住宅价格影响的空间分布图

② 到最近CBD的距离(CBD)。到最近地铁站的距离的回归系数取值在−0.380~0.584，均值为0.176，标准差为0.015。从其影响程度的空间格局中可看出(图3)，这一解释变量存在一定的空间异质性，且在研究区域大部分地区中回归系数为负，表明距离CBD越近，对房价的提升作用越显著。

Figure 3. Spatial distribution of CBD effects on housing prices

图3. CBD对住宅价格影响的空间分布图

③ 到最近公园的距离(PARK)。到最近公园的距离的回归系数取值在−0.177~0.08，均值为−0.044，标准差为0.023。在蒲江县、邛崃市、彭州市、大邑县、都江堰市、崇州市等地这一变量的回归系数为正，代表着距离公园越远对房价提升作用越强，但这种提升作用较为微小；而在龙泉驿区、双流区和武侯区回归系数为负，表明离公园越近对住宅价格的提升作用越强，相较于其他区域而言，这类区域显然对城市公园绿地有更高的需求，因此公园对住宅价格也就有更为明显的提升作用。

5.3.2. 区位因素

① 到最近公交站的距离(BUS)。到最近公交站的距离的回归系数取值在−0.428~0.208，均值为−0.153，标准差为0.038。从其影响程度的空间格局中可看出(图4)，这一变量影响程度显著且存在空间异质性，在金牛区、成华区少部分地区呈现距离公交站越远，价格越高的空间分异特征；而其余地方包括青羊区、郫都区和龙泉驿区等地则是距离公交站越近，对住宅价格的提升作用越大。

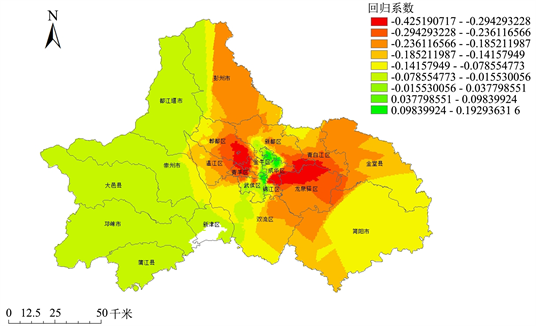
Figure 4. Spatial distribution of BUS effects on housing prices

图4. BUS对住宅价格影响的空间分布图

② 到最近地铁站的距离(METRO)。到最近地铁站的距离的回归系数取值在−0.801~0.504，均值为−0.089，标准差为0.02。从其影响程度的空间格局中可看出(图5)，在研究区域大部分地区，如双流区、武侯区和青羊区等地都是距离地铁站越近，对住宅价格的提升作用越强。这一片区是成都的高新区，选择在这片区域购房的消费者更多考虑的是通勤的便利性，因此距离地铁的越近，对房价的提升作用也就越强。

往往而言，距离公交站和地铁站的远近能反映出从一定程度上衡量一个楼盘的区位因素是否优越，交通是否便利，因此到公交站的距离和到地铁站的距离是影响住宅价格的重要因素。

5.3.3. 结构因素

① 物业管理费(COST)。物业管理费的回归系数取值在0.005~0.185，均值为0.061，标准差为0.116。物业管理费在研究区域具有内有正向的提升作用，这意味着物业管理费越高，住宅价格越高。在空间分布上而言(图6)，影响程度呈现东高西低的趋势。这同时也体现出当前成都市的住宅价格的影响因素更加偏向于向“舒适性”发展，一般而言物业管理费的高低与物业管理服务水平和小区环境是呈正比，越高的物业管理费往往也就代表着高质量的服务。物业管理费对房价的显著提升作用间接也证明了成都市居民对更舒适、更安全居住环境的迫切需要。

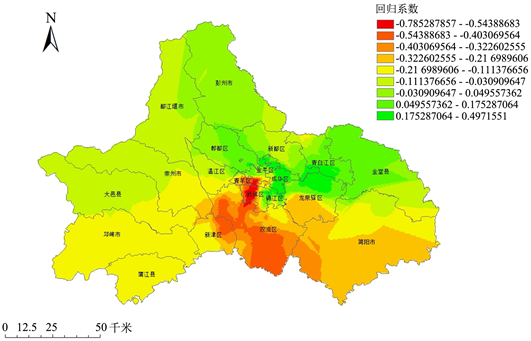
Figure 5. Spatial distribution of METRO effects on housing prices

图5. METRO对住宅价格影响的空间分布图

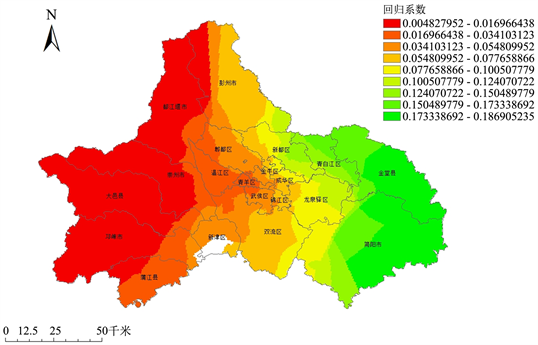
Figure 6. Spatial distribution of COST effects on housing prices

图6. COST对住宅价格影响的空间分布图

② 建筑面积(AREA)。建筑面积的回归系数取值在−0.035~0.127，均值为0.041，标准差为0.179。从其影响程度的空间格局中可看出(图7)，建筑面积这一变量影响程度显著且在大邑县、蒲江县、邛崃市等地呈现负向影响，而在成都主城区和简阳市金堂县等地呈现正向影响。在金牛区、成华区等地，建筑面积对于房价具有显著的正向提升作用，在诸如此类的主城区当中，土地出让价格高，对改善型住房的需求较为旺盛，也就造成了住宅的建筑面积越大，单价越高的现象。

③ 容积率(FAR)。容积率的回归系数取值在−0.006~0.095，均值为0.037，标准差为0.0.239。容积率在研究区域大部分地域内对住宅价格具有一定正向提升作用，在大邑县、都江堰市和崇州市等地有着微弱的负向影响。容积率对住宅价格的影响与物业管理费对住宅价格的影响在空间分布上较为相似，其对于住宅价格的提升作用也呈现东高西低的趋势。

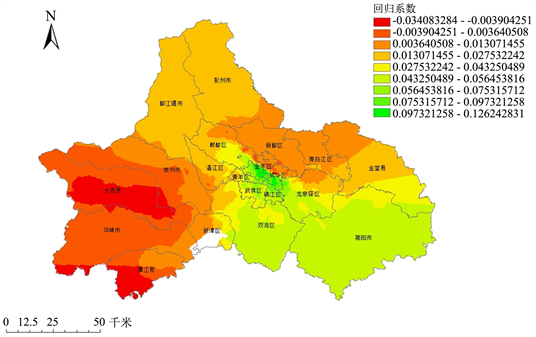
Figure 7. Spatial distribution of AREA effects on housing prices

图7. AREA对住宅价格影响的空间分布图

④ 卧室个数(BED)。卧室个数的回归系数取值在−0.058~0.061，均值为0.011，标准差为0.2。卧室个数对于住宅价格的影响具有一定的空间异质性，在简阳市、金堂县、青羊区、金牛区以及温江区，卧室个数这一解释变量有较高的负向影响作用，也就是说，卧室个数越多，房价相对而言更低；而在新津区、双流区、龙泉驿区、新都区的部分区域，卧室个数对于住宅价格则有正向提升作用；在大邑县、常州市、都江堰市等地卧室个数对住宅价格的影响则较为微弱。

6. 结论和讨论

本文充分考虑了住房价格这一样本数据对于邻里因素、区位因素和结构因素的空间依赖性，将GWR模型运用到成都市住房价格空间分异特征以及影响因素的研究上，并采用ArcGIS中的Kriging插值法对GWR的计算结果进行了可视化分析。基于GWR的模型推演结果，可以得出以下结论：与OLS模型拟合优度相比，GWR模型拟合优度更高，在处理诸如住宅价格这样的空间数据上更为精确可靠；成都房价在空间分布上呈现圈层结构形态，而在金堂县以及简阳市呈现多核心分布形态；根据GWR回归结果可对各解释变量的影响程度排序：HOS > CBD > BUS > METRO > COST > PARK > AREA > FAR > BED。总体而言，在成都市住宅市场房价的影响因素中，邻里因素的影响程度最大，然后是区位因素，最后才是结构因素。

在高新区离地铁站越近，房价越高，在此区域投资可优先选择近地铁站的黄金地段。建筑面积和卧室个数对于武侯区、金牛区、青羊区、锦江区和成华区内住宅价格存在正向提升作用。物业管理费对研究区域全域呈正向影响，这表明成都市居民对于住房的消费需求正由生活便利性转为生活质量型。主城区内高昂的房价导致多数人购买的都是刚需型房源，且主城区内尚存在“老破小”房型，消费者对于改善型房源的需求较大。开发商在拿地时可以考虑建造容积率低，建筑面积大的改善型楼盘，以适应市场的需求。成都市房价高值区主要位于双流区、武侯区行政区域内的高新区地段，最高单价已达4万/²，针对这样的情况，成都市政府一是应考虑出台政府指导价以控制房价，二是应考虑在地铁口附近修建人才公寓，公租房或廉租房，对土地实行集约利用、高密度开发，以满足“蓉漂”对于住宅的迫切需求。在新津区、大邑县、都江堰市、蒲江县、邛崃市、彭州市、大邑县等区县应完善医院、公园和CBD等公共设施配套，满足居民日益增长的对高质量生活的追求。

本文样本数据因国家政策改动，没有选择成交价，而是挂牌价，虽然能一定程度上反应住宅价格的空间分异特征和各因素对其的影响，但挂牌价由于存在价格偏高或偏低的现象，因此会造成一定的误差。本研究运用GWR模型探究了各因素对住宅价格的影响，后续研究可将此模型也可用于对住宅价格、商业用地价格等方面的研究上。且不同的物业类型，其影响因素可能不一样，后续可考虑继续完善指标体系。

基金项目

本项目得到西南民族大学研究生创新型科研项目(项目编号：YB2022269)资助。