1. 引言
近年来大规模洪涝灾害时有发生,其中2019年南方六省大规模降雨、2021年河南特大暴雨较为严重。大规模洪涝灾害初期各受灾点物资需求量大,而供应点物资储备量有限,受灾点物资需求紧迫度的研究,可提高应急物资高效分配。
宋英华等 [1] 以受灾地区人口密度、受伤受困人数比例、老幼人口比例、应急物资需求量、基础设施损坏程度为指标建立地震灾后受灾点物资需求紧迫度评价体系。陈雨珊 [2] 等从确诊数、确诊率、死亡率、出院率维度构建重大邀请下应急物资需求紧迫度模型。王付宇等 [3] 以受灾地区感染人数衡量疫情下各受灾点物资需求紧急度。张莉 [4] 等采用熵值法研究重大公共卫生事件医疗应急物资受灾点需求急迫度。本文在构建受灾点物资需求紧迫度评价指标体系基础上,利用层次分析–熵值法确定指标权重,采用B型关联-TOPSIS法量化需求紧迫度。
2. 应急物资需求紧迫度评价指标体系
无论是自然灾害类突发事件,还是大规模公共卫生事件,物资需求紧迫度评价体系大都围绕灾情、人口和物资三方面建构。《洪涝灾情评估标准》以死亡人口、受灾人口、农作物受灾面积、直接经济损失、倒塌房屋数量、水利设施经济损失、骨干交通中断时长、城市受淹时长、生命线工程中断时长、级别场次灾害数量等为评价指标。结合郑州“7·20”特大暴雨具有降水强度大、影响范围广、短时降水量大,受灾范围大、城市内涝严重、河流水库险情频发等特点。综合借鉴参考文献 [1] [2] 的物资需求紧迫度评价体系和《洪涝灾情评估标准》等评价指标,确定以受灾面积、单日降水量、物资需求量、物资库存量、人口密度、死亡人数为受灾点物资需求紧迫度评价指标,如图1所示。其中受灾面积属于数值明确型指标,受灾面积越大,灾害损失越大,应急物资需求越紧迫。单日降水量属于数值明确型指标。单日降水量越大,受灾点爆发洪水、泥石流等灾害风险越大,应急物资需求越紧迫。物资需求量属于数值明确型指标,如救生圈、救生衣等生命救助类物资;如急救药品,消杀药品等生命支持类物资;如帐篷、食品、饮用水等临时住宿类物资;应急物资需求量越大需求越紧迫。物资库存量属于模糊型指标,物资库存量越少,应急物资需求越紧迫。人口密度属于数值明确型指标。人口密度越大,灾害损失越大,应急物资需求越紧迫。伤亡人数属于数值明确型指标。伤亡人数越多,灾害危害越大,应急物资需求越紧迫。
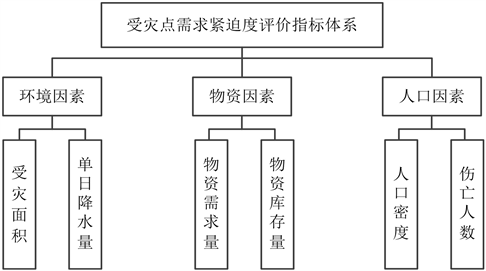
Figure 1. Evaluation index of material demand urgency at the disaster site
图1. 受灾点物资需求紧迫度评价指标
3. 应急物资需求紧迫度评价指标量化
指标对评价对象和评估结果影响程度选择主客观相结合方法确定指标权重,主观评价方法采用层次分析法 [5],客观评价方法采用熵值法 [6]。
郑州“7·20”特大暴雨,受灾较为严重的市县:郑州市、巩义市、新郑市、新密市、荥阳市、登封市、中牟县,各受灾点基本情况如表1所示 [7]。

Table 1. Basic data of disaster-affected points
表1. 受灾点灾情基本数据
3.1. 层次分析法确定指标权重
1) 构造判断矩阵。根据三角模糊数分别用数字3、5、7、9表示受灾点物资库存量比较少、少、很少、非常少。判断矩阵如表2所示。
2) 计算权向量。将判断矩阵归一化处理,得到标准判断矩阵值
,
,其中
为判断矩阵原始值;将标准判断矩阵按行求和值
,
;对和值归一化处理得到指标权重
,
。如表3所示。

Table 2. Judgment matrix with analytic hierarchy process
表2. 层次分析法判断矩阵
3) 一致性检验。最大特征值
计算,
,得
;一致性指标
计算,
,得
;一致性比例
衡量,
,其中
为随机一致性指标,若
说明判断矩阵通过一致性检验反之说明判断矩阵没有通过一致性检验,六阶矩阵
标准值为1.26,得
,
通过一致性检验。
3.2. 熵值法确定指标权重
1) 指标确定性转化。7个受灾点,6个评价指标组成原始数据指标体系
,使用三角模糊数对评价指标中现有物资库存量进行确定性转化。
2) 数据标准化处理,
,其中
归一化数据;
指标原始数据。
3) 计算各指标熵值
。
4) 计算各指标差异性系数
。
5) 计算权重
,如表4所示。

Table 3. Weight of each index with AHP
表3. 层次分析法各指标权重

Table 4. Weight of index with entropy method
表4. 熵值法各指标权重
3.3. 层次分析–熵值法线性加权确定指标权重
层次分析法赋权主观随意性较大,熵值法赋权依据客观指标离散程度,难以完全反映指标间内在规律。综合主观、客观赋权间的互补性,线性平均加权求其组合权重,即可减少层次分析法主观性过强的影响,又可改善熵值法过于客观的影响。如表5所示。

Table 5. Weight of each index with linear weighting method
表5. 线性加权法各指标权重
4. 受灾点物资需求紧迫度量化
灰色B型关联法客观性较强 [8]。TOPSIS法可对评价指标优劣排序,简洁灵活,但主观性较强 [9]。综合灰色B型关联和TOPSIS分析法,弥补各自缺陷,增加决策有效性。
1) 建立加权规范化矩阵。将线性平均加权组合权重[0.0500 0.1652 0.1996 0.0720 0.1251 0.3881]与标准化矩阵A相乘得到加权标准化矩阵B。
2) 确定指标正理想解
;负理想解
,其中
为各指标列向量。
3) 计算B型关联度。正理想解B型关联度
: ,其中
,其中
,
;同理计算负理想解的B型关联度
。
4) 计算相对贴近度
。
5) 计算需求紧迫系数
。如表6所示。

Table 6. Urgency coefficient of material demand in disaster areas
表6. 受灾点物资需求紧迫系数
5. 结论
郑州“7·20”暴雨洪涝灾害受灾点物资需求紧迫度评价指标体系中排名前三指标是伤亡人数、物资需求量和单日降水量,权重分别为0.3881、0.1996、0.1652。七个主要受灾点中,郑州市物资需求紧迫系数为0.1601,紧迫度相对最高,其次是巩义市和荥阳市,物资需求紧迫系数分别为0.1514、0.1525,中牟县物资需求紧迫系数为0.1295,紧迫度相对最低。因此,救援相关部门可依据受灾点应急物资需求紧迫度高低,优先、合理、高效分配应急物资。
基金项目
湖南省社会科学基金项目(17YBA003),湖南省教育厅重点项目(19A010)。