Python在信号与系统教学中的应用

Applications of Python in Teaching of Signals and Systems

摘要: 信号与系统是电子科学与技术、通信工程、控制理论与控制工程等专业学生的必修课程，商业软件Matlab作为一种强大的信号处理和科学计算工具被很多高校应用于信号与系统课程教学中；然而随着国际局势的持续恶化，我国部分高校已无法在教学和科研中继续使用Matlab，因此亟需探索替代方案。本文将主要探索在信号与系统教学中用Python替代Matlab的可行性，并通过实例验证Python在电路时频域分析、信号滤波、信号抽样恢复中的实用性，为信号与系统教学从Matlab平台向开源的Python平台的顺利转移提供支撑。

Abstract: Signals and Systems is a compulsory course for undergraduate students majoring in electronic science and technology, communication engineering, control theory and control engineering, etc. As a powerful signal processing and scientific computing tool, the commercial software Matlab is widely used in the teaching of Signals and Systems courses in many colleges and universities. However, with the continuous deterioration of the international situation, some universities in China have been forbidden from using Matlab in teaching and scientific research. Hence, it is urgent to explore alternative solutions. This paper will explore the feasibility of using Python to replace Matlab in the teaching of Signals and Systems, and verify the practicability of Python in time and frequency domain analysis of electronic circuits, signal filtering, and Nyquist sampling theorem, so as to provide supports for a smooth transfer of Signals and Systems teaching from the Matlab platform to the open-source Python platform.

1. 引言

当今世界已经进入信息时代，信息成为社会、经济发展的“血液”、“润滑剂”，因此现代信息技术广泛地渗透到通信、计算、传感等领域，并改变着人们的生活学习和工作；在此过程中信息产业也逐步成为全球最大的产业。而信号与系统这门课程是信息技术的基础，是各大高等院校电子信息大类、控制工程大类等工科学生的必修课程，也是学生进入工作岗位需掌握的基础技能。

在信号与系统教学中，很多高校把Matlab作为一个辅助工具在课堂上帮助学生理解概念并掌握具体方法，相对传统教学方式，这种基于Matlab的信号与系统教学方式取得了很好的效果 [1]。然而在新时代国际关系背景下，随着中国科技的不断发展和快速进步，某些国家为了保持自身优势而限制我国在诸多领域的发展。2020年5月，美国商务部宣布将33家中国公司和机构列入实体名单，而这33家机构中除了一些科技企业之外还有一众高校，比如哈工大、哈工程、北航等多所高校被禁止使用美国的Matlab软件。其它高校虽然暂时被允许使用Matlab，但头上的“达摩克利斯之剑”已经高悬，必须未雨绸缪提前考虑替代方案。

Python作为一种开源的程序语言，近些年在信号处理、矩阵运算、机器学习等领域得到广泛的应用，其开源性、易学性、以及拥有强大的第三方库等特点为在信号与系统教学中替代Matlab奠定了坚实的基础。首先，Python多样化的编程方式具有灵活、代码简洁、易入门等特点 [2]；其次，Python程序可以在不同系统平台上运行且不必修改源代码，可移植性较强，C/C++可以作为扩展库被Python调用且Python也能内嵌到C/C++等程序之中，而在Matlab中这些功能难以实现。另一方面不少高等院校在本科生大一或大二阶段开设了Python程序语言相关课程，为信号与系统教学中Python的使用建立了基础。

Python的第三方库NumPy为数组和矩阵的快速计算提供了与Matlab类似的功能，拥有更快的数据收集、组织与处理能力；SciPy建立在NumPy上，大量地使用了NumPy的数组，它的不同子模块对应于不同的应用，比如插值、积分、优化、图像处理、特殊函数等，提供了多样化数值计算、传递函数分析等信号处理方法；SymPy是一个符号计算库，应用于算术、微积分、代数、离散数学、量子物理等领域，可以替代Matlab的相关功能 [3]。因此，选择Python作为信号与系统课程学习的实践平台，一方面可以紧跟时代步伐，另一方面可以增强学生的语言编写能力，拓展学生的思维，让学生在实践中学习信号与系统理论知识。

本文作者将探讨在信号与系统教学中使用Python替代Maltab的可行性，并展示如何用Python编程语言帮助学生掌握电路仿真分析、信号滤波原理、采样定理等知识点。最终实现在教学中通过Python的强大功能把信号与系统课程具象化，并引导学生把理论与实践深入结合，激发学生学习的积极性。

2. Python在信号与系统教学中替代Matlab可行性分析

信号与系统这一课程具有概念抽象，性质繁多和公式推导复杂等特点，它主要包含了信号与系统在不同变换域的分析方法 [4] [5]，如时域、频域、复频域等。单纯的数学公式无法直观的向学生展现信号处理过程中所包含的物理特性。因此，需要通过在实践中以可视化的方式展示信号变换和处理的具体过程，并清晰地描述信号在不同变换域中的映射关系。这时候借助Python让学生从理论走向实践能够大大降低这一课程的抽象性和学习难度。

Matlab作为集数值分析、矩阵运算、信号处理和图形展示于一体的科学计算平台，其强大的图形可视化能力能够绘制信号在不同变换域的示意图，帮助理解各种变换的物理特性。另外Matlab内置了大量的数学函数，例如信号与系统课程中常用的卷积运算、傅里叶变换以及拉普拉斯变换均能够通过内置函数快速实现，这能够帮助学生从繁重的手工数学运算中解脱出来，将学习重点转向对课程中关键概念和原理的深入理解与应用。同时Matlab内置工具包(例如滤波器设计工具包Filter Designer、Simulink等仿真工具)能够帮助实现滤波器设计及系统仿真等一系列需求。

毫无疑问Matlab作为信号与系统这一课程辅助教学工具能够帮助教师更生动地讲解课程，帮助学生更好地理解课程，并且国内也有着很多高校使用Matlab作为教学辅助工具。然而，Matlab作为教辅工具仍存在许多现实问题。Matlab作为一款商用付费软件，需要支付极其昂贵的授权费，这对一般学生来说是难以承受的，并且即使是学校支付高昂的授权费获得授权，也面临着随时被禁止使用的风险。另一方面Matlab作为商业软件其代码完全不开源，类似于“黑盒”，学生只能单纯调用，而无法获知内部实现方法，而Python的开源特性允许学生查看具体功能函数的实现代码，这为想进一步深入钻研信号与系统这门课的学生提供了难得的机会 [6] [7] [8]。

Python作为一种开源的程序语言，其丰富的第三方扩展库基本涵盖了Matlab在信号与系统教学中所涉及的功能。例如NumPy可以完成所有Matlab矩阵运算功能。SciPy提供包括频谱分析，滤波器设计等多种典型信号处理方法。Matplotlib对应Matlab中绘图功能。SimuPy扩展包能够完成Matlab中Simulink所实现的仿真功能。在运行速度方面，尽管Matlab运算速率稍快于Python [9]，但随着Python算法不断更新，运算速度已经相差不大，而且作为信号与系统教学的教辅工具，对运算速度并不敏感。在代码编写方面，Python语言更加简洁，其开放的项目社区为初学者提供了较低学习门槛以及丰富的学习资源，开源的第三方函数库为解决实际问题提供了有力支撑 [10]。Python与Matlab作为信号与系统教辅工具详细对比如表1所示。因此，无论在功能上，成本上，学习难度上，Python作为信号与系统教学辅助工具替代Matlab也无疑是可行的。

Table 1. Comparison between Python and Matlab as a teaching tool for Signals and Systems

表1. Python与Matlab作为信号与系统教辅工具对比

3. 基于Python的信号与系统实验仿真实例

3.1. 谐振电路的时频域分析

本节我们将演示如何通过Python对RLC谐振电路做频域和时域仿真分析。图1为信号与系统课程中均会分析的RLC电路图，通过拉普拉斯变换学生可以推导出其传递函数 $H\left(s\right)$ 如公式(1)所示。

Figure 1. The RLC series circuit

图1. RLC谐振电路图

$H\left(s\right)=\frac{y\left(s\right)}{u\left(s\right)}=\frac{Rs}{L{s}^2+Rs+\frac{1}{C}}$ (1)

学生可以通过式(1)在Python中通过选择电阻、电感、电容值计算RLC电路的频谱响应。在此实例中为了将谐振频率设为 $f_0=\frac{1}{2\text{π}\sqrt{LC}}=10\text{kHz}$，电感、电容、电阻的取值分别为L = 15.92 μH, C = 15.92 nH。

为了获得不同的Q值，电阻 分别取100 Ω、200 Ω、400 Ω。对应的幅频响应和相频响应可以通过Matplotlib绘制出来，如图2所示。通过观察不难发现其幅频响应呈现出带通滤波器的特性，而且随着R变大，Q变小，通带带宽不断增加。

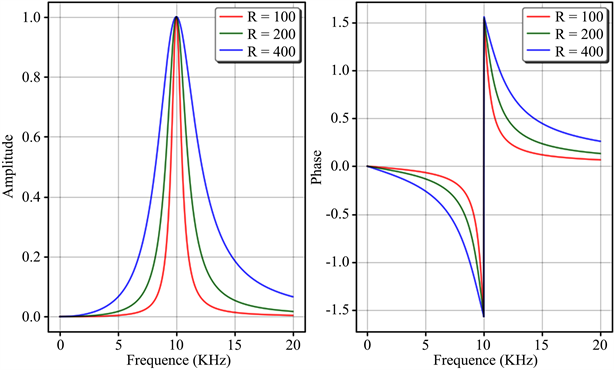
Figure 2. The frequency response of the RLC circuit

图2. RLC电路幅频和相频响应曲线

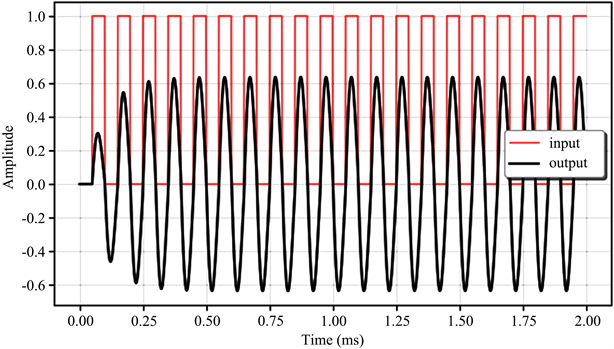
Figure 3. The time-domain response of the RLC circuit

图3. RLC时域响应

为了进行时域分析，RLC电路的激励源设定为幅度为1 V，脉冲宽度为50 μs，占空比为50%的矩形波，然后通过Python中SciPy.lsim函数进行时域仿真，lsim可以实现对线性时不变系统求解，其输入参数为激励信号和系统传递函数，其中系统传递函数可以是多项式形式、零极点形式、或状态空间方程。本实例中采用如式(1)所示的多项式形式。考虑到激励信号矩形波由直流分量和1、3、5、7等高次谐波组成，经过中心频率为10 kHz的带通滤波器后，只有频率为10 kHz的一次谐波出现在输出端，而直流分量和高次谐波均被滤掉，如图3所示。

本实例展示了基于Python的时频域分析将枯燥的公式和概念转换为生动的实例，增强了学生的参与感，也为学生提供了一个强大的工具帮助其更深入的了解RLC谐振电路的频域和时域特性。

3.2. 巴特沃斯滤波器分析

本节我们将说明如何通过Python设计一个巴特沃斯带通滤波器，并实现对时域信号的滤波功能。巴特沃斯滤波器的主要特点是通频带内的幅频响应较为平坦，相频响应单调递减。巴特沃斯滤波器的幅频响应可以表示为：

$H\left(\omega \right)=\frac{1}{\sqrt{1+{\left(\frac{\omega }{{\omega }_c}\right)}^{2n}}}$ (2)

式中n为滤波器的阶数，ω_c是−3 dB截止频率。为了实现对以下信号进行滤波

$\begin{array}{c}x\left(t\right)=0.05\sin \left(2.4\text{π}t\right)+0.01\cos \left(424\text{π}t+0.1\right)+0.02\cos \left(1200\text{π}t+0.011\right)\\ +0.03\cos \left(4000\text{π}t\right)\end{array}$ (3)

以获得角频率为1200π (频率为600 Hz)的余弦信号，我们需要设计一个带通滤波器允许600 Hz信号通过，阻止式(3)中其它频率信号。这里我们选择通带频率为300~900 Hz，带通滤波器的设计可以使用SciPy.signal中butter函数，输入其上下限截止频率，得到巴特沃斯带通滤波器的传递函数，图4为不同阶数的滤波器对应的幅频响应，可以看出巴特沃斯滤波器阶数越高，其过渡带越窄。

Figure 4. The magnitude response of Butterworth bandpass filters with different orders

图4. 不同阶数巴特沃斯带通滤波器的幅频响应

此实例中选用9阶滤波器对式(3)中的信号进行滤波，然后将butter函数输出的传递函数以及原始数据输入SciPy.signal中lfilter函数进行滤波。滤波完成后，我们通过Matplotlib.pyplot画图来观察带通滤波器对式(3)中信号的滤波效果，如图5所示。本例中使用Python实现了巴特沃斯带通滤波器的设计和时域滤波的功能，另外SciPy工具包也支持很多其它种类滤波器的设计，为学生提供多样性的实践机会。

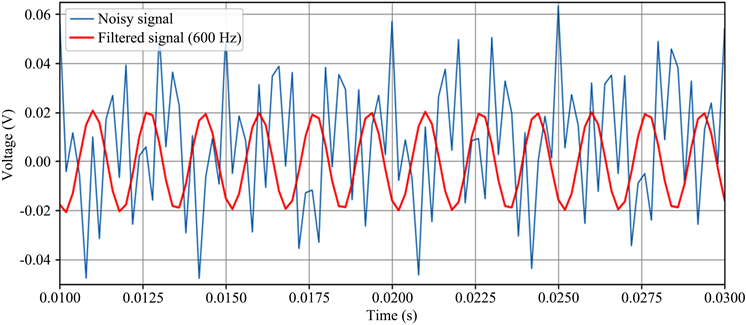
Figure 5. The output of the Butterworth bandpass filter

图5. 巴特沃斯带通滤波器滤波效果图

3.3. 信号采样及恢复

本节将演示如何通过Python对信号进行采样及恢复。图6(上)所示的待抽样的信号是一个频率f = 20 Hz的正弦函数，根据奈奎斯特采样定理若要恢复此信号，采样频率至少大于待抽样信号频率的两倍，因此我们使用两倍于待抽样信号的频率进行采样f_s = 40 Hz。图6(中)为采样后的样本信号，为了恢复原始信号，我们首先使用SciPy.signal工具设计截止频率f_c = 25 Hz的低通滤波器，然后使用SciPy.signal中的lsim函数进行时域仿真从而滤除采样信号所含的高次谐波。恢复出来的信号如图6(下)所示，可以发现恢复后的信号与原始信号几乎一致。本实例可以帮助学生更好的理解奈奎斯特采样定理，并且生动的展示了信号采样和信号恢复过程。

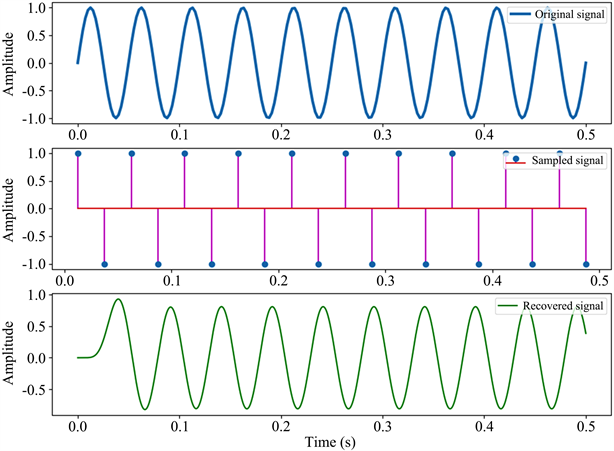
Figure 6. Sampling and reconstruction of signals

图6. 信号的采样与恢复

4. 教学效果

通过实践教学发现，得益于Python的入门难度较低，基于Python教辅工具的信号与系统课程教学课堂与基于Matlab的信号与系统教学课堂相比，学生成绩优秀与良好的百分比略有提高，如图7所示。因此验证了信号与系统教学中可以使用Python来替代Matlab的可行性，也证明了Python与信号与系统的结合更能激发学生的兴趣，提高学生的参与度，课堂效率也更高。

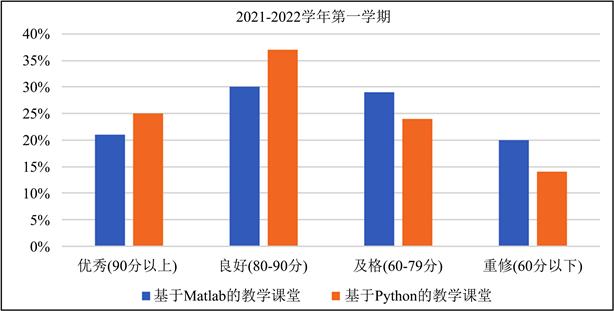
Figure 7. Comparison of student achievements between Matlab- and Python-based Signals and Systems teaching

图7. 基于Matlab和Python的信号与系统教学学生成绩对比

5. 小结

本文以信号与系统课程中的谐振电路时频域分析、巴特沃斯滤波器设计、采样定理为例，验证了Python在信号与系统课程中拥有较好的教学效果，证明了Python在信号与系统课程中作为教学辅助设计工具能够替代Matlab。基于Python的信号与系统课程教学是“实践与理论紧密结合”“还教于学”等思想在实践中的贯彻和落实。它将抽象复杂的电路分析、信号处理等知识转换为可编程的应用实例，让学生能参与其中，起到拓展学生思维、开发学生潜能、提升学生编程能力的作用。