1. 引言
随着工业的高速发展,对直线电机的控制要求也越来越高 [1]。与一些旋转电机如滚珠丝杠、联轴器经过传动件后再变成直线相比,永磁同步直线电机的系统响应时间更短 [2] [3] [4]。但又由于在直线电机运动的传动系统中都没有任何缓冲的环节,存在的各种可能的机械扰动或因素像各种非线性机械摩擦运动和线性机械摩擦振动,都会大大影响整个直线电机整体的正常运动轮廓 [5] [6]。永磁同步直线电机具有体积小,效率高等优点,而广泛应用于交流伺服系统中。现在采用传统的比例积分微分(proportion integral derivative, PID)控制。虽然PID控制方法简单并且方便调速,在一定的范围内能够达到控制的需求,但在外部干扰过大时,就难以满足控制要求 [7] [8]。滑模控制逐渐运用在永磁同步电机控制中 [9],文献 [9] 将滑模控制与电机的直接转矩控制结合,改善了系统的运行性能。文献 [10] 设计了一种积分离散滑模速度控制器来代替速度外环的PI控制器,并且将负载观测器作为前馈补偿。干扰观测器的基本思想是将实际的干扰和参数变化等所产生的实际对象与理想对象之间的差异等效到控制的输入端,就可得到等效干扰,然后可以在控制中加入等效的补偿,从而对干扰进行抑制 [11]。文献 [11] 运用干扰观测器设计出一种运动轨迹跟踪控制器。文献 [12] 将H∞和干扰观测器的复合控制器减少在磁悬浮轴承–转子系统在高速工作时的干扰。
本文针对永磁同步直线电机的运动轮廓问题,结合SMC和DOB提出了一种运动轮廓的控制方法,首先建立永磁同步直线电机的数学模型,然后给出运动轮廓控制器的具体实施方法。最后在Simulink平台将永磁同步直线电机建立仿真模型,并进行仿真分析,通过对比不同控制策略的仿真结果,验证了方案的有效性。
2. 永磁同步直线电机数学建模
直线电机的驱动原理和旋转电机的驱动原理比较相似,都是通过导条切割磁场产生推力,不同之处在于旋转电机需要中间传动机构将旋转运动转换为直线运动,而直线电机直接通过直线运动驱动工作台。直线电机结构演变过程,将旋转电机沿径向剖开,然后将转子、定子沿直线铺展,旋转电机的定子演变成初级,动子演变成次级。
本文研究的对象是永磁直线同步电机,在直线电机建模时,为了能降低耦合度,也为了更加方便的分析和求解数学模型方程,使用相同步旋转坐标系。由于在直线电机中电感和磁链具有强耦合关系,并且它还具有许多复杂的变量,所以在建立数学模型前,做出以下的假设:
1) 直线电机所在温度变化对直线电机的工作影响忽略不计;
2) 直线电机上的三项绕组成对称分布,并且在空间上相差,忽律电机运行过程中而产生的磁动势;
3) 绕组的自感和互感始终保持不变;
4) 忽略直线电机的一些损耗,如磁滞,铁芯和涡流;
5) 直线电机的定子空载电势呈正弦波,忽略磁场高次谐波。
dq坐标系建立在永磁体上,d轴与永磁体的磁感应线重合,坐标随着永磁体的转动相对于动子旋转。其数学模型可以由三相静止坐标系下的数学模型通过Clark变换和旋转变换得来。
(1)
式(1)中,
,
分别为直线电机d轴和q轴电压;
和
分别为直线电机d轴和q轴的电流;
为绕组的等效电阻;
和
分别为d轴和q轴磁链幅值矢量;
同步磁场的旋转角速度。
永磁同步直线电机的同步磁场的旋转角速度:
(2)
式(2)
表示永磁体极距;
则表示永磁同步直线电机的同步速度。
永磁同步直线电机的磁链方程为:
(3)
式(3)中
表示永磁体励磁基波磁链;
和
分别为直线电机d轴和q轴线圈的电感。所以其电磁推力表达式为:
(4)
式(4)
中是电磁推力,对永磁同步直线电机而言,
。电磁推力表达式可简化为:
(5)
式(5)
中是电磁推力系数。
直线电机的机械运动方程为:
(6)
式(6)M中为运动部件的总质量;f是运动系统中的干扰力;B为直线电机的黏性阻尼。
如果在矢量控制中使用的控制策略,则可以将永磁同步直线电机的数学模型简述为:
(7)
根据上面的分析,可表示出直线电机的位置环和速度环的传递函数:
(8)
(9)
在该数学模型中没有将推力波动,端部效应,摩擦力等考虑到永磁同步直线电机中。所以将这些非线性因素作为干扰,所以在控制器设计时将消除这些干扰作为基本原则。
3. 运动轮廓控制器设计
为了提高运动系统抗干扰的能力,采用滑模控制器和干扰观察器相结合的方式来设计运动轮廓控制器。用滑模控制来取代传统的PID控制,并用干扰观察器来对外部干扰进行有效抑制。
3.1. 滑模控制器设计
滑模控制(sliding mode control, SMC)是的本质是一种变结构的控制方法,自从上世纪50年代被提出了后就广泛应用于各种控制系统中。并且滑模控制中的滑动模态可以设计,与系统参数无关。因此滑模控制具有良好的鲁棒性。滑模控制的一般设计思路为滑模面的设计和趋近律的设计,还有最后控制器的求解。
滑模控制原理如图1所示,直线为滑模面,不同的滑模控制有着不同的滑模面,目前滑模面主要有线性滑模控制、终端滑模控制、积分滑模控制等等。滑模面设计时部件要选择合适的设计方法,还要考虑控制系统的结构和特点,设计合适的滑模面。本文选择的是积分滑模控制,
。状态轨迹线受到滑模控制器的作用使它趋近于滑模面,并且沿着滑模面收敛到原点。
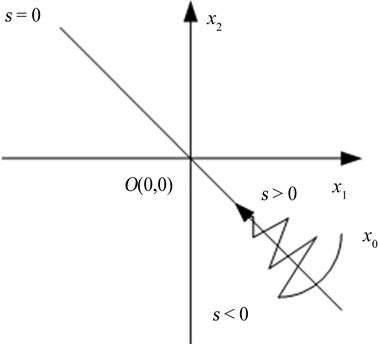
Figure 1. Scheme of sliding mode control
图1. 滑模控制基本原理
滑模面设计的基本思想是让系统的状态轨迹进入滑动模态后具有逐渐稳定的较好动态特性。
取PMLSM系统的状态变量为
(10)
式(10)中
和v分别是给定的直线电机的速度和实际的速度。
结合式(7),并对
、
求导可得到
(11)
然后设计系统的滑模面s为
(12)
并对t求导可得
(13)
滑模运动主要包括趋近运动和滑模运动两个过程,可以通过趋近律来改善这两个过程。趋近律设计的主要目的是让系统的状态轨迹能够在合理的时间内趋近于滑模面并且维持在上面运动。本文采用指数趋近律来设计控制器,在趋近过程中,指数趋近律的趋近速度是变化的,到达切换面之前,趋近速度比较快,减少了时间;到达切换面时,趋近速度变小,抖振被减弱了。
(14)
结合式(13),式(14)可得
(15)
由式(15)可得
(16)
则控制量
的滑模控制器结构流程图如图2所示。
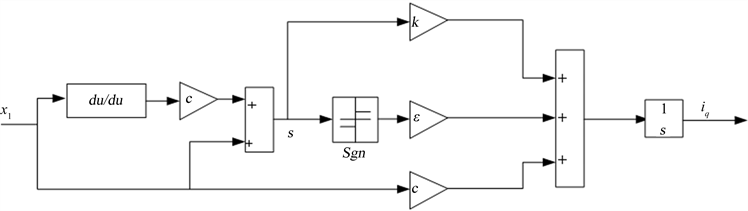
Figure 2. Sliding mode controller structure diagram
图2. 滑模控制器结构流程图
3.2. 干扰观测器设计
为了更加提高永磁同步直线电机控制系统的抗干扰能力,并且考虑到有无法准确进行数学建模的干扰存在。干扰观测器(Disturbance observer, DOB)可以将实际的干扰和参数变化等所产生的实际对象与参考模型之间的差异等效到控制的输入端,就可得到等效干扰,然后可在控制中加入等效的补偿,从而对干扰进行抑制。干扰观察器在1987年由日本学者首次提出,其核心思想是,将被控对象的实际输出与名义模型的输出间的差异作为等效干扰,并将其补偿到控制输入端,从而消除外界干扰对系统控制性能的影响。在实际控制系统中,由于模型中有不确定性、参数摄动、外界干扰等因素的影响,大多都需要设计的控制器具有一定的鲁棒性。而基于干扰观测器的控制框架能够有效消除上述因素所带来的干扰。干扰观察器的原理图如图3所示:
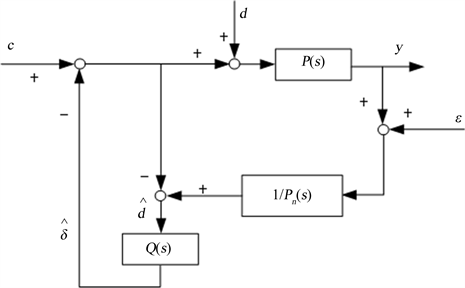
Figure 3. Scheme of disturbance observer
图3. 干扰观测器原理图
图中c是输入的信号;d是外部干扰;P(s)为对象的传递函数;Pn(s)则为传递函数的名义模型;ξ表示测量噪声;Q(s)则表示低通滤波器。
首先可以先假设
,来方便说明干扰观测器的原理和作用,则有:
(17)
然后经过干扰观测器补偿后,输出量y可表达成:
(18)
由式可知,如果将干扰补偿后,实际输入与输出之间可以满足传递函数的名义模型。由图可知,输出y的表达式为:
(19)
其中
;
;
。
根据上述公式可知若滤波器
为低通滤波器时,
,则
、
、
,表明干扰观察器对外界干扰d能够很好抑制作用。所以滤波器用三阶低通滤波器,即:
(20)
上式中对应截止频率,与抑制外部干扰的能力有关,当
的值越小,其在低频时的抑制能力越强,在高频时减弱;反之,当
的值越大,其在低频时的抑制能力变弱,在高频时
增强。截止频率要在鲁棒性和抗干扰能力之间寻找,根据经验取
。
将干扰观测器与滑模控制器结合变成运动轮廓控制器如图4所示。
4. 仿真与分析
4.1. 建立仿真
MATLAB是美国公司MathWorks开发的一款商业数学软件,它主要用于算法开发、数据可视化、
数据分析及数值计算的高级技术计算机语言和交互式环境。Simulink是MATLAB重要的模块之一。它是利用图形化的工具进行建模仿真的,可以实现动态系统建模、仿真和综合分析的集成环境,它支持系统设计、仿真、自动代码生成以及嵌入式系统的连续测试和验证。在Simulink中,系统为用户提供了各式各样的模块库,在建立由差分方程和微分方程构成的系统仿真模型时,用户只需从含有各种典型环节子模块的模块库中方便的选择需要的模块,实现Simulink仿真系统的构建。用户只需要通过鼠标简单操作就可以构建成各种各样的系统模型。永磁同步直线电机的结构如图5所示:
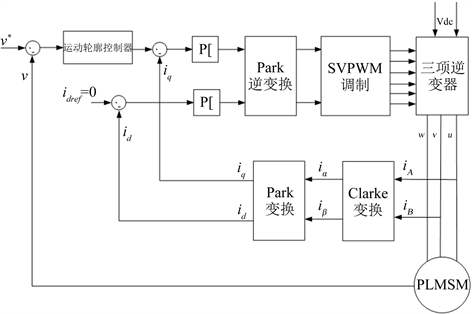
Figure 5. Controller structure of permanent magnet synchronous linear motor
图5. 永磁同步直线电机的结构
为了验证所提出的运动轮廓控制器的有效性和可行性,将所提出的方案与传统PID控制相比较,在Simulink仿真平台上建立永磁同步直线电机模型,并进行仿真。调速系统采用
的矢量控制方法,永磁同步直线电机的具体参数为
,
,
,
,
。并且给定速度参考为0.3 m/s。
4.2. 结果分析
为了验证本文提出的方法的有效性。在Simulink平台中将图5中的运动轮廓控制器换成PID和滑模控制,再观察它们的输出的速度图,和速度误差,以验证方案的可行性。
图6(a)和图6(b)分别是在PID控制下直线电机系统启动的速度和速度的误差,在速度达到给定参考速度后,最大的速度误差在0.002 m/s。由于PID控制精度较低,而且没有对外部干扰进行抑制,所以产生了较大的运动轮廓误差。
 (a)
(a)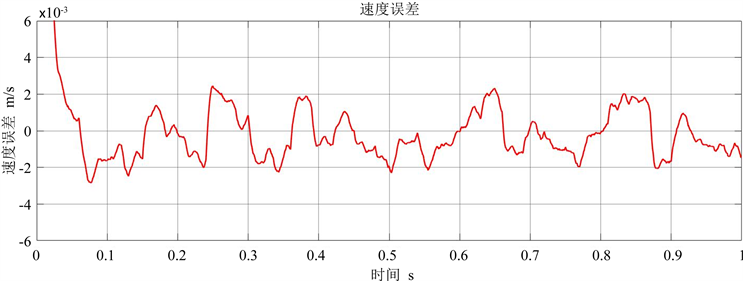 (b)
(b)
Figure 6. (a) The speed of the motion platform (PID only); (b) Speed error (PID only)
图6. (a) 运动平台的速度(仅PID);(b) 速度误差(仅PID)
 (a)
(a)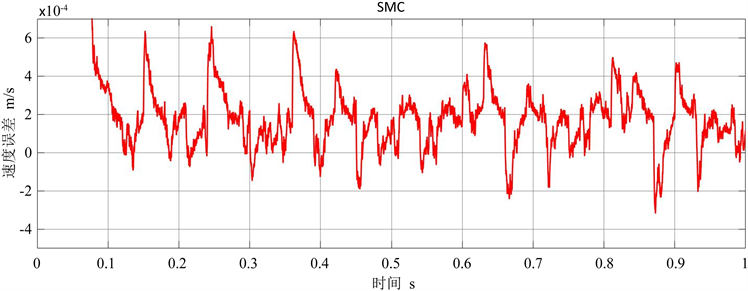 (b)
(b)
Figure 7. (a) The speed of the motion platform (SMC only); (b) Speed error (SMC only)
图7. (a) 运动平台的速度(仅SMC);(b) 速度误差(仅SMC)
 (a)
(a) (b)
(b)
Figure 8. (a) The speed of the motion platform (SMC + DOB); (b) Speed error (SMC + DOB)
图8. (a) 运动平台的速度(SMC + DOB);(b) 速度误差(SMC + DOB)
图7(a)和图7(b)分别是SMC控制下直线电机系统启动的速度和速度的误差,在达到给定参考速度后,最大的速度误差在0.0006 m/s。SMC的控制精度比PID控制要高。
图8(a)和图8(b)分别是SMC + DOB控制下直线电机系统启动的速度和速度的误差,当速度达到给定参考速度后,最大的速度误差在0.0004 m/s。干扰观测器能够有效的对外部干扰进行了有效的补偿,所以控制误差减小了。
5. 结论
为了提高永磁同步直线电机的运动精度,减少外部干扰的影响,实现对永磁同步直线电机运动轮廓的控制,本文提出一种将滑模控制和干扰观察器相结合的运动轮廓控制器。首先将永磁同步直线电机的数学模型建立,在选择好合适的滑模控制方法,本文选择的是积分滑模控制,指数趋近律,作为反馈控制。再建立好干扰观察器模型,减少外部干扰,提高运动精度,最后通过在Simulink平台进行仿真。通过对PID控制,SMC控制和SMC + DOB控制,不同控制器的控制系统进行仿真,然后再将这些结果对比分析。
通过对上面的三种控制方法的仿真结果对比可以看出,本文提出的将滑模控制器和干扰观察器相结合的运动轮廓控制器的运动轮廓最好,系统的速度误差最小,最大速度误差在0.0004 m/s,该控制器的控制精度比较理想,验证了该方案的有效性。
致谢
感谢与我并肩作战的舍友与同学们,感谢关心我支持我的朋友们,感谢学校领导、老师们,感谢你们给予我的帮助与关怀。