可叠加的随机微分方程软件可靠性模型

Additive Stochastic Differential Equations Software Reliability Models

摘要: 随着软件系统规模的不断扩大，大多数复杂软件系统都由多个组件构成，组件的可靠性影响软件系统的可靠性。在实际中，软件故障跟踪系统中故障的报告存在随机性、不规律性以及各种不确定因素，因此故障检测过程可以看作是一个随机过程。本文应用伊藤型随机微分方程建立软件可靠性模型，利用各组件的故障数据来建立叠加的随机微分方程可靠性模型，对模型参数进行估计。最后，将两组实际软件项目的数据集应用于所提出的叠加随机微分方程可靠性模型，结果表明所提出的叠加随机微分方程可靠性模型有更优的效果。

Abstract: With the increasing scale of software systems, most complex software systems are composed of multiple components, and the reliability of the components affects the reliability of the software system. In practice, there are randomness, irregularity and various uncertainties in the reporting of faults in software fault tracking systems, so the fault detection process can be regarded as a sto-chastic process. In this paper, the Itô type stochastic differential equation (SDE) is applied to build a software reliability model, and the fault data of each component is used to build a superimposed stochastic differential equation reliability model and to estimate the model parameters. Finally, data sets from two real software projects are applied to the proposed superposed stochastic differ-ential equation reliability model, and the results show that the proposed superposed stochastic dif-ferential equation reliability model has better results.

1. 引言

近年来，计算机迅速发展，已经深入到人们生活的各个方面，大到国家系统小到日常生活。计算机软件也在不断的发展更新中，一旦计算机软件发生故障，就会对人们的生活和工作造成影响甚至可能造成巨大损失。例如2021年11月24日，阿里云在Web服务器软件阿帕奇下发现重大漏洞，该漏洞可能导致设备远程受控，引发敏感信息窃取、设备服务中断等严重危害，属于高危漏洞。这些由软件失效造成的影响不胜枚举，告诉我们软件可靠的重要性。

当前最常用的一类模型是基于NHPP的软件可靠性模型，该模型的特点是假设累计故障数服从非齐次泊松过程。原始的NHPP类模型是G-O模型，其后相继提出了Delayed S-shaped、Inflection S-shaped以及Yamada等经典模型，为后续的研究提供重要的参考。Wang等 [1] 考虑故障检测与修正过程的时间相关性，结合了故障检测和修正过程建立软件可靠性模型，进行了数值实例研究；Kapur等 [2] 考虑了测试团队在测试过程中不断获得的测试工作和知识等因素，提出了基于测试工作量的软件可靠性模型；Jain等 [3] 引入多变点，在考虑不完全调试、测试工作函数和故障减少因子的基础上建立软件可靠性增长模型。以上NHPP模型都是在经典模型的基础上，结合不完美排错、测试工作量以及变点等进行研究。后续研究学者引入随机微分方程来建立软件可靠性模型。Tamura等 [4] 考虑开源软件的活跃状态，提出了基于随机微分方程的开源软件可靠性模型，并根据总逾期软件维护工作量找到开源软件的最佳升级时间；Singh等 [5] 为了适应故障跟踪系统故障报告现象的不规则状态和噪声的不规则波动，应用伊藤型随机微分方程建立了故障跟踪系统的可靠性模型；Zhang等 [6] 针对故障检测率可能会受到某些因素的影响，并且可能会随着时间的推移在某个时间点发生变化这一问题，提出了具有变化点的随机微分方程软件可靠性模型来精确反映故障分布的变化；Tamura等 [7] 考虑云计算中网络流量和大数据，提出了一个具有二维Wiener过程的跳跃扩散模型来评估云软件的稳定性。Fang等 [8] 采用随机微分方程对软件故障检测过程进行置信区间估计，为软件开发人员和测试人员进行软件开发和软件质量控制提供了有益的信息；Wang等 [9] 考虑软件调试过程中主观和客观的影响、故障排除的难度和复杂性、故障之间的依赖关系、软件测试不同阶段的变化、测试进度等因素，考虑到软件调试过程中故障引入率的不规律变化，提出了一种不完全软件调试模型；Chatterjee等 [10] 针对开源软件开发了基于随机微分方程的软件可靠性增长模型，并考虑到故障分类的影响，制定了多版本的软件可靠性增长模型，并通过平衡可靠性水平最大化和产品开发成本最小化来获得产品的最佳发布日期；Chatterjee等 [11] 考虑软件故障的严重程度以及各故障被修复的优先级不同等因素，建立了一种基于随机微分方程的软件可靠性模型，将故障检测与故障发生的严重程度联系在一起，并将纠正故障的过程与缺陷修复的优先级联系在一起；Singh等 [12] 考虑软件故障修复、功能增强和添加新功能等情况，给故障排除率带来了不确定性，使用三维维纳过程定义了三种波动类型，提出了一个统一的模型框架。综上，目前的随机微分方程可靠性模型都是结合经典模型和随机微分方程对总故障数据建模，但对复杂的系统软件，未考虑多组件叠加模型的情况。

本文针对提出的想法，基于各组件的故障数据建立叠加随机微分方程可靠性模型来估计总故障数据。其余部分主要内容如下：第二节主要介绍了经典NHPP类软件可靠性模型，以及叠加的随机微分方程可靠性模型的框架；第三节针对真实数据进行数值案例分析；最后一节给出结论。

2. 随机微分方程可靠性模型

2.1. 软件可靠性模型

软件可靠性模型是一种随机过程模型，将软件可靠性与失效时间、故障数等相关的量联系在一起。目前软件可靠性模型有多种，其中非齐次泊松过程(NHPP)类模型应用广泛。

NHPP类软件可靠性增长模型的假设如下 [13]：

1) 软件失效过程满足非齐次泊松过程；

2) 系统剩余的缺陷引起软件的失效；

3) 排除过程中不会引入新的缺陷。

记 $N\left(t\right)$ 为 $\left(0,t\right]$ 时间段内检测出的累计故障数， $\left\{N\left(t\right),t\ge 0\right\}$ 是一个独立增量过程； $m\left(t\right)$ 表示到t时刻累计故障数的期望值， $E\left[N\left(t\right)\right]=m\left(t\right)$ ； $\lambda \left(t\right)$ 为失效强度函数，表示单位时间内发现的故障数。有上述假设可知：

$\frac{\text{d}m\left(t\right)}{\text{d}t}=b\left(t\right)\left[a-m\left(t\right)\right]$ (1)

其中a表示软件预期的故障总数， $b\left(t\right)$ 为故障检测率函数，表示t时刻软件中潜伏的每个故障被检测到的概率。求解微分方程后可得：

$m\left(t\right)={\text{e}}^{-{\displaystyle {\int }_0^{t}b\left(u\right)\text{d}u}}\left[m\left(0\right)+a{\displaystyle {\int }_0^{t}b\left(u\right){\text{e}}^{{\displaystyle {\int }_0^{t}b\left(u\right)\text{d}u}}\text{d}u}\right]$ (2)

令 $m\left(0\right)=0$，可简化均值函数为：

$m\left(t\right)=a{\text{e}}^{-{\displaystyle {\int }_0^{t}b\left(u\right)\text{d}u}}\left[m\left(0\right)+a{\displaystyle {\int }_0^{t}b\left(u\right){\text{e}}^{{\displaystyle {\int }_0^{t}b\left(u\right)\text{d}u}}\text{d}u}\right]$ (3)

对于多组件构成的软件系统，可利用各组件的故障数据来建立叠加模型。考虑软件包含k个组件的情况，需要建立可叠加的可靠性模型，其基本假设为：

1) 软件包含k个组件(子系统、对象或其他)；

2) 对象i的失效过程服从NHPP， $\left\{N_i\left(t\right),t\ge 0\right\}$，其均值函数为 $m_i\left(t\right)$ ；

3) $\left\{N_i\left(t\right),t\ge 0\right\}\left(i=1,2,\cdots ,k\right)$ 相互独立；

4) 软件的累积故障数为 $N\left(t\right)$，可知：

$N\left(t\right)={\displaystyle {\sum }_{i=1}^k{N}_i\left(t\right)}$ (4)

其均值函数为： $m\left(t\right)={\displaystyle {\sum }_{i=1}^k{m}_i\left(t\right)}$。

对公式(4)中的故障检测率 $b\left(t\right)$ 取不同的形式，可以得到不同的NHPP模型，经典的模型如下：

1) 当 $b\left(t\right)=t$ 时，得到经典的GO模型，其均值函数为：

$m\left(t\right)={\displaystyle {\sum }_{i=1}^k{a}_i}\left(1-{\text{e}}^{-b_{i}t}\right)$ (5)

2) 当 $b\left(t\right)=\frac{b^{2}t}{1+bt}$ 时，得到经典的DSS模型，其均值函数为：

$m\left(t\right)={\displaystyle {\sum }_{i=1}^k{a}_i}\left(1-\left(1+b_i\right){\text{e}}^{-b_{i}t}\right)$ (6)

2.2. 可叠加的随机微分方程软件可靠性模型

考虑故障追踪系统中故障报告的随机性、不规律性以及各种不确定因素，故障检测过程可以看作是一个随机过程，用随机微分方程来建立相应的软件可靠性模型 [5]。由前文的假设可以得到：

$\frac{\text{d}N\left(t\right)}{\text{d}t}=r\left(t\right)\left[a-N\left(t\right)\right]$ (7)

其中 $r\left(t\right)$ 可能含有不规则波动，因此可以得到： $r\left(t\right)=b\left(t\right)+\delta \gamma \left(t\right)$， $\delta$ 是一个表示不规则波动的正常量， $\gamma \left(t\right)$ 为标准的高斯白噪声。

将 $r\left(t\right)$ 带入公式(7)可以得到：

$\frac{\text{d}N\left(t\right)}{\text{d}t}=\left[b\left(t\right)+\delta \gamma \left(t\right)\right]\left[a-N\left(t\right)\right]$ (8)

公式(7)可以被扩展成下面的伊藤类随机微分方程：

$\text{d}N\left(t\right)=\left[b\left(t\right)-\frac{1}{2}{\delta }^2\right]\left[a-N\left(t\right)\right]\text{d}t+\delta \left[a-N\left(t\right)\right]\text{d}W\left(t\right)$ (9)

其中 $W\left(t\right)$ 表示与 $\gamma \left(t\right)$ 有关的一维维纳过程，因此故障总数函数可以表示为：

$N\left(t\right)={\displaystyle {\sum }_{i=1}^k{N}_i\left(t\right)}={\displaystyle {\sum }_{i=1}^k{a}_i}\left[1-{\text{e}}^{-{\displaystyle {\int }_0^t{b}_i\left(u\right)\text{d}u}-{\delta }_{i}W\left(t\right)}\right]$ (10)

当 $b\left(t\right)$ 分别取不同的取值时，可以得到基于GO模型的可叠加随机微分方程可靠性模型(GO_ASDE)以及基于DSS模型的可叠加随机微分方程可靠性模型(DSS_ASDE)：

$N\left(t\right)={\displaystyle {\sum }_{i=1}^k{a}_i}\left[1-{\text{e}}^{-b_{i}t-{\delta }_{i}W\left(t\right)}\right]$ (11)

$N\left(t\right)={\displaystyle {\sum }_{i=1}^k{a}_i}\left[1-\left(1+b_{i}t\right){\text{e}}^{-b_{i}t-{\delta }_{i}W\left(t\right)}\right]$ (12)

因此，模型的均值函数分别为：

$E\left[N\left(t\right)\right]={\displaystyle {\sum }_{i=1}^k{a}_i}\left[1-{\text{e}}^{-b_{i}t+\frac{1}{2}{\delta }_i^{2}t}\right]$ (13)

$E\left[N\left(t\right)\right]={\displaystyle {\sum }_{i=1}^k{a}_i}\left[1-\left(1+b_{i}t\right){\text{e}}^{-b_{i}t+\frac{1}{2}{\delta }_i^{2}t}\right]$ (14)

3. 数值案例

为了充分、有效地评估提出的改进模型的拟合和预测性能，本节使用了经典模型GO模型、DSS模型以及本文改进模型GO_ASDE、DSS_ASDE的均值函数，使用真实数据集进行计算，对计算结果进行对比分析。模型汇总见表1：

Table 1. Model summary table

表1. 模型汇总表

3.1. 数据介绍

3.1.1. 数据集1

数据集1的故障数据来自Eclipse故障跟踪系统(https://bugs.eclipse.org/bugs/)中的AspectJ项目，AspectJ是Eclipse基金组织的开源项目，它是Java语言的一个面向切面编程(AOP)的实现，是最早、功能比较强大的AOP实现之一，可以在Eclipse Foundation 开源中使用，既可以单独使用，也可以集成到Eclipse中。

AspectJ的主要数据字段有：Compiler、IDE、LTWeaving、Docs、AJBrowser、AJDoc、Ant、Build、Library、Rutime和Testing等，以月为单位进行数据整合。表2是各组件在2005年1月到2020年11月期间检测到的故障数(共191组数据，只展示部分数据)，其中F1表示组件Compiler的累计故障数，F2表示组件IDE的累计故障数，F3表示组件LTWeaving的累计故障数，剩余8个组件的故障数相对较少，F4表示其他8个组件的累计故障数之和，F为总累计故障数。

Table 2. The faults data of AspectJ (Dataset1)

表2. AspectJ故障数据(数据集1)

3.1.2. 数据集2

数据集2的数据来自Eclipse故障跟踪系统(https://bugs.eclipse.org/bugs/)中的Babel项目，Babel是一个JavaScript编译器，使软件开发者能够以偏好的编程语言或风格来写作源代码，并将其利用Babel翻译成JavaScript。

Babel的主要数据字段有：Plugins、Website、EnglishStrings、Translation和Server，以月为单位进行数据整合，表3是各组件在2008年1月到2016年12月的期间检测到的故障数(共108组数据，只展示部分数据)。其中F1表示组件Plugins的累计故障数，F2表示组件Server的累计故障数，F3表示组件Website的累计故障数，F4表示组件EnglishStrings和Translation的累计故障数之和，F为总累计故障数。

Table 3. The faults data of AspectJ (Dataset2)

表3. AspectJ故障数据(数据集2)

3.2. 模型评价指标

为了比较各模型的性能，选择以下评价指标进行衡量 [14]：AIC，MSE。

1) AIC信息准则：AIC是衡量模型优良性的一种标准，其定义为 $\text{AIC}=2K-2\log \left(L\right)$，其中K为参数数量，L为极大似然值。当误差服从正态分布时，可得：

$\text{AIC}=2K+m\log \left(\frac{\text{RSS}}{m}\right)$ (15)

其中m为样本容量，RSS为残差平方和。

2) MSE：均方误差，更小的MSE有更好的拟合效果。其定义为：

$\text{MSE}={\displaystyle {\sum }_{j=1}^m\frac{{\left(m\left(t_j\right)-m_j\right)}^2}{k}}$ (16)

其中 $m\left(t_j\right)$ 表示到时刻 $t_j$ 系统累计故障数的估计值， $m_j$ 表示到时刻 $t_j$ 系统累计观测到的故障数。

3.3. 参数估计结果

3.3.1. 数据集1结果

使用表2中AspectJ真实数据集对经典模型和本文模型进行参数估计，参数估计结果及评价指标见表4。

Table 4. Parameter estimation results for Dataset 1

表4. 数据集1的参数估计结果

从表4中可以看出：对于经典模型，GO模型的MSE和AIC要小于DSS模型，更适合AspectJ的故障数据；针对GO模型来说，本文改进后的叠加随机微分方程模型的效果要优于经典GO模型。从结果可以看出利用随机微分方程建立的叠加模型的效果要比经典模型要好，这也说明了把故障检测过程可以看作是一个随机过程，用随机微分方程来建立相应的软件可靠性模型是合理且有效的。四个模型的累计故障数的拟合结果如图1所示，各模型的RE图如图2。

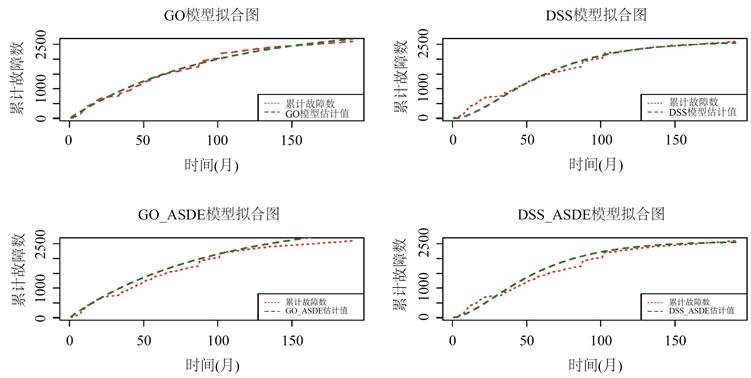
Figure 1. Fitted plots of the cumulative number of failures for each model

图1. 各模型的累计故障数拟合图

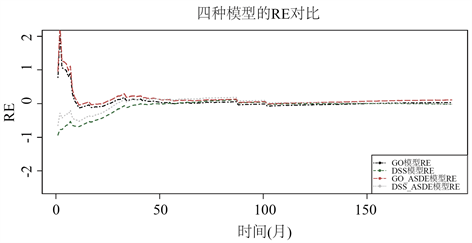
Figure 2. RE comparison chart for each model

图2. 各模型的RE对比图

3.3.2. 数据集2结果

使用数据集2的Babel真实数据进行估计，参数估计结果及模型的评价指标结果如表5所示。

对于经典模型，GO模型更适合该数据，MSE和AIC均小于DSS模型。同时改进后的叠加随机微分方程GO模型、DSS模型的效果均优于经典的GO模型、DSS模型。从结果可以看出把故障检测过程看作随机过程来建立软件可靠性模型是合理且有效的。四个模型的累计故障数的拟合结果如图3所示，各模型的RE图如图4。

Table 5. Parameter estimation results for Dataset 2

表5. 数据集2的参数估计结果

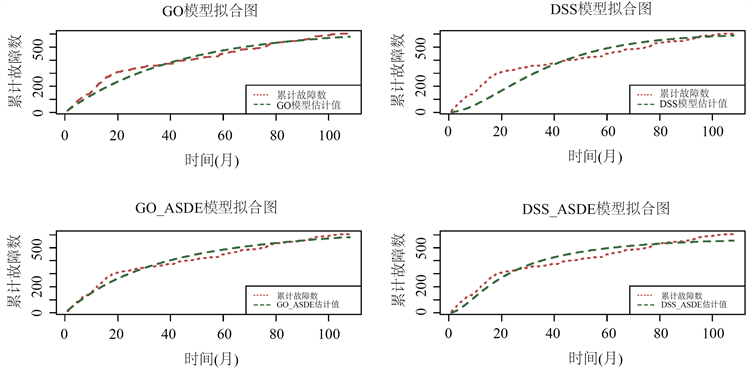
Figure 3. Fitted plots of the cumulative number of failures for each model

图3. 各模型的累计故障数拟合图

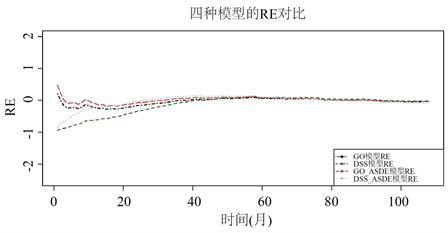
Figure 4. RE comparison chart for each model

图4. 各模型的RE对比图

4. 结论

在多组件的软件系统中，软件系统的可靠性估计十分重要，估计各组件的可靠性也是不可或缺的。实际中，软件可靠性分析所需的故障数据大多来自软件的故障跟踪系统，该系统上报告的软件故障存在随机性和不确定性，会导致故障检测率会受一些随机影响。因此本文针对多组件软件系统，考虑软件故障报告的随机性情况，利用组件的故障数据来建立软件可靠性叠加模型，将经典的NHPP类软件可靠性模型改进为叠加的随机微分方程软件可靠性模型，度量软件系统可靠性的同时也可以对各个组件的可靠性做一个度量。从Eclipse故障跟踪系统上获得了AspectJ项目和Bebel项目的故障数据，通过分析对比发现叠加的随机微分方程可靠性模型的效果优于经典的NHPP类软件可靠性模型，该模型度量了每个组件的可靠性情况以及整体的可靠性，且拟合效果更好。

基金项目

国家自然科学基金资助项目(71901078)；贵州省电力大数据重点实验室(黔科合计Ｚ字[2015] 4001)。

NOTES

^*通讯作者。