基于多元统计分析的黑胫病烟草叶绿素含量高光谱估测

Hyperspectral Estimation of Chlorophyll Content of Tobacco Influenced by Phytophthora parasitica var. nicotianae Based on Multivariate Statistical Analysis

摘要: 为快速有效地评估烟草病害等级，需要合理准确地估计烟草叶绿素含量。分别利用ASD Field Spec4地物光谱仪和HSY-051叶绿素仪测定黑胫病烟草旺长期叶片高光谱及其SPAD值，以叶片光谱原始反射率及其8种变换处理分别与叶绿素含量进行相关分析，然后利用多元统计分析方法(逐步回归和主成分回归)分别建立叶绿素含量估测模型。结果表明：1) 原始光谱的8种变形与叶绿素含量的相关性都高于原始光谱反射率；2) 各变换的一阶导数和二阶导数与叶绿素含量的相关性都明显高于其原始形式；3) 利用逐步回归方法建立的模型估测效果最好，其决定系数R²为0.8715。经验证，模型精度较好。本研究可为高光谱技术监测烟草叶片叶绿素含量提供一定的参考。

Abstract: The content of chlorophyll is a very important assessment index in the growing situation of to-bacco. Thus, estimating the content of chlorophyll in tobacco accurately is effective for rating to-bacco disease. By use of the ASD Field Spec4 spectrometer to determine hyperspectral data of tobacco leaves infected by Phytophthora parasitica var. nicotianae in the vigorous growing period and HSY-051 chlorophyll meter to measure the SPAD value. Then, the correlation analysis of chlorophyll content with hyperspectral reflectance and its eight transforms was proceeded. On this basis, the chlorophyll content estimation models were established with the method of multivariate statistical analysis (stepwise regression and principal component regression). The results indicate that 1) the correlation between chlorophyll content and the eight transforms of original spectra was higher than that of the original spectral reflectance; 2) the correlation between chlorophyll content and the first derivative or second derivative of each transform was significantly higher than that of original form; 3) the best model was: Y = 22.415 + 39249.31X₁ − 13943.06X₂ − 24807.33X₃ + 296102.44X₄ − 309086.89X₅ + 130909.69X₆ − 7751.45X₇, and this model with a correlation coefficient of 0.9335 and R2 of 0.8715 was based on stepwise regression. After verification, the precision of the model is good. Therefore, the research will provide a reference for the better application of hyperspectral technology in monitoring the chlorophyll content of tobacco leaves.

1. 引言

烟草黑胫病(Phytophthora parasitica var. nicotianae)是烟草生长过程中危害最为严重的病害之一，它主要通过土壤传播，大田一旦侵染，往往会造成成片烟株凋萎死亡，给烟农带来巨大的损失 [1] [2] [3]。因此，及时掌握烟草黑胫病的发生情况对病害防治具有重要意义，它可以指导烟农对已发病区域及时进行隔离，同时做好未发病区域的防御工作。烟草侵染黑胫病后的一个明显特点是烟叶变黄萎蔫，叶绿素含量减少。而叶绿素是叶片中吸收光能的物质，不仅在植物进行光合作用是必不可缺的因素之一，也是作为植物生长过程中的重要生化参数，它在植被的生长过程、光合能力和营养状况等方面扮演了重要的指示器 [4]。所以，叶绿素含量是作物长势监测中一项非常重要的评估内容，合理准确地估计黑胫病烟草叶绿素含量，对快速有效地评估烟草病害等级，合理进行烟草病害评估具有重要作用。传统的叶绿素测定方法一般采用分光光度法，此方法优点是可以准确地测定叶绿素含量，但同时也存在很大的局限性，操作费时费力、难以实现实时、快速、无损和大面积监测；而高光谱遥感作为一种实时、快速、无损监测技术，可在不破坏作物的条件下，实现对作物生长及营养状况的快速监测 [5]。而且，叶绿素含量和高光谱反射率之间有着直接联系，因此，基于遥感的叶绿素含量监测研究已被广泛展开 [6] [7] [8] [9]。Daughtry [10] 利用两类冠层光谱植被指数研究了叶绿素含量；Hansen [11] 利用偏最小二乘回归方法研究了458~884 nm之间的植被指数与叶绿素之间的关系并建立了反演模型；杨峰等利用高光谱遥感技术研究了不同生长期下小麦与水稻两种作物的叶绿素含量和冠层光谱之间的变化，将两种作物的叶绿素含量与其冠层光谱数据间的相关性进行比较，进而确定了监测两种作物叶绿素含量的最佳植被指数 [12]；杨杰等通过修正光谱指数建立了水稻上部叶片叶绿素含量的高光谱估算模型 [13]；金林雪等研究了植物光谱指数和叶片含水量及绿度特征值的相关关系，确定了叶片水分和SPAD值的光谱指数或最佳波段 [14]；李敏夏等分析了苹果叶片高光谱特征与叶绿素含量和SPAD值的关系，研究了叶片的SPAD值和叶绿素含量与微分光谱之间的相关性 [15]；李方舟等做了基于高光谱数据的水旱地冬小麦叶绿素含量监测 [16]，取得了比较理想的结果。此外，李凤秀、彭彦昆、汤旭光等众多研究者对作物的叶绿素含量进行了模型的建立、并进行了反演，取得了较好的效果 [17] [18] [19]。

逐步回归是一种较为常用的统计方法。当被预测变量(因变量)为一个，预测变量(自变量)有多个时，我们可以采用逐步回归的方法建立模型。该方法的优点是所有自变量都会被逐个考虑，对提高预测准确度无贡献或贡献极小的自变量会被淘汰；当自变量间存在相关性时，贡献小的自变量会被淘汰。因此，能够用较少的自变量来建立模型，但模型的预测准确度不会比用所有自变量建立的模型低。主成分回归也可以用来建立多重回归模型，其基本思路是提取所有自变量的主成分(注：原始自变量数目不会减少)，用主成分来构建回归方程。由于原始自变量间可能存在自相关，自变量太多反而会影响预测的准确度，所建立的模型可能还不如逐步回归的准确度高。

综上所述，国内外已有众多学者研究利用高光谱技术监测小麦、玉米、水稻、苹果等的叶绿素含量，但对烟草叶绿素含量高光谱监测的研究还比较少，因此该研究具有一定的现实性和必要性。本研究利用逐步回归和主成分回归分析两种多元统计分析方法，探讨黑胫病烟草原始光谱反射率及其一阶微分、二阶微分等8种变换处理与叶绿素之间的关系，建立叶绿素含量最佳估测模型，从而为烟草黑胫病监测提供有效手段。

2. 材料与方法

2.1. 材料、仪器

试验于2015年在山东沂水的沂城镇和道托镇进行，供试品种为NC102，烟草种植和田间管理由当地烟草公司统一实施。试验于烟草旺长期，选择黑胫病发病典型地块进行实地数据采集，两个乡镇共选择六个病害小区，每个小区分别选择60株典型发病植株进行数据采集。其中5个小区用于建立模型，1个小区用于验证模型。

地物波谱仪ASD Field Spec4 (美国ASD公司)，配有ViewSpecPro光谱处理软件；HSY-051叶绿素测定仪(杭州汇尔公司)。

2.2. 黑胫病植株的高光谱测量

采用ASD Field Spec4便携式地物波谱仪进行黑胫病植株光谱反射率数据的测定，ASD Field Spec4地物波谱仪的测量波长范围为350~2500 nm，其中，350~1050 nm 采样间隔为1.4 nm，光谱分辨率为3 nm，1000~2500 nm采样间隔为2 nm，光谱分辨率为10 nm。观测时必须选在晴朗无云无风的天气，测定时间应选在北京时间11:00~14:00。测量时，传感器探头垂直正对烟株，高度设置为1 m，每株烟测量3次，每次记10组数据，最后取其平均值作为冠层光谱。测定过程中，每隔10株用标准白板矫正一次白板，确保测量结果的准确性。

2.3. 叶绿素含量测定

研究表明植物叶绿素含量和叶片绿色度(SPAD)值具有明显的相关性，SPAD值能够表现植物叶绿素含量的变化，因此，利用叶绿素测定仪测定的SPAD值在一定条件下可代替叶绿素含量的直接测定，使用叶绿素测定仪测定植物叶绿素含量是完全可行的 [20]。本研究中叶绿素含量的测定是利用HSY-051叶绿素测定仪(单位：SPAD)。测量过程中，为提高测量精度，应在每株烟草的上部、中部和下部各选择一片叶，每片叶上分叶尖、叶中、叶基三个部位左右两侧各测量三次，然后取其平均值作为该叶片的叶绿素含量，最后取上中下三片叶片的54个数据作为该烟株的叶绿素含量。

2.4. 数据处理方法

将每株烟采集的光谱数据利用光谱处理软件ViewSpecPro剔除异常值后求取平均值并输出dat文件，在光谱采集过程中，由于外界环境的影响以及光谱仪不同波段对能量响应上的差异，会导致光谱曲线存在一些噪声，为减少噪声影响提高建模精度，必须对光谱数据进行平滑处理。常用的方法有移动平均法、拟合多项式法、小波变换及各种回归平滑方法 [21]。研究选用九点平滑处理方法来去除光谱曲线噪声影响 [22] 其数学表达式为：

$\begin{array}{c}{R}_i=0.04\times R_{i-4}+0.08\times R_{i-3}+0.12\times R_{i-2}+0.16\times R_{i-1}+0.2\times R_i\\ +0.16\times R_{i+1}+0.12\times R_{i+2}+0.08\times R_{i+3}+0.04\times R_{i+4}\end{array}$ (1)

九点平滑处理完成后，再分别求取原始光谱反射率的一阶导数、二阶导数、对数以及对数的一阶微分和二阶微分、平方根以及平方根的一阶微分和二阶微分 [23]。将以上数据与叶绿素含量进行相关分析，筛选出相关性最高的光谱变量。最后利用DPS建立叶绿素含量的估测模型。以SPAD值为因变量，各种光谱指数及其衍生值为自变量，进行逐步回归，得到预测模型。以所有自变量进行主成分分析，然后进行主成分回归，得到主成分回归模型。将六个病害小区分为6组，其中5组数据(300个)用于建立模型，1组数据(60个)用于对模型进行验证，利用Excel2003和DPS进行数据分析并作图。

3. 结果与讨论

3.1. 黑胫病烟草叶片原始光谱及8种变换与叶绿素含量相关性分析

在Excel 2003中完成原始光谱8种变换的计算并与叶绿素含量进行相关分析，各相关性的横向对比图如图1所示。

由图1可以看出，原始光谱的8种变形与叶绿素的相关性都高于原始光谱反射率，各种变换的一阶导数和二阶导数与叶绿素相关性都明显高于其原始形式，这表明微分处理可以增加光谱信息量，为利用

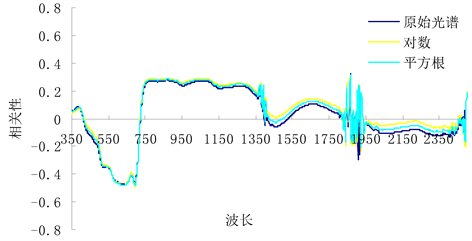
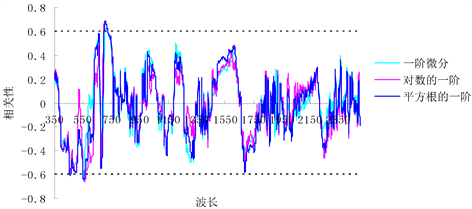
Figure 1. Correlation analysis of original spectrum and its eight transformations with chlorophyll content

图1. 原始光谱及其8种变换与叶绿素含量相关分析

微分处理技术估测作物叶绿素等生理生化参数提供了基础。因此，在选择建模因子时可以将原始光谱以及原始光谱的对数和平方根舍弃。分别对比各变换的一阶微分和二阶微分，可以看出一阶微分和二阶微分内部的变化趋势基本一致；对比一阶微分和二阶微分可以看出，二者与叶绿素相关性较高区域集中在450~750 nm之间。将6种微分变换的相关系数绝对值最大的反射率筛选出来作为建模备选因子，具体结果见表1。

Table 1. The highest correlation combination between transformation forms and chlorophyll

表1. 各变换形式与叶绿素相关性最高组合

表1显示，经过对数和平方根变换后的一阶微分与二阶微分与叶绿素相关性绝对值的最大值都高于原始光谱的一阶微分和二阶微分，表明对数和平方根变换有放大局部光谱信息的作用。

3.2. 黑胫病烟草叶绿素含量估测模型

3.2.1. 基于逐步回归的叶绿素含量估测模型

将各变换相关性绝对值大于0.64的数据挑选出来作为可供选择变量，经统计共有76个可供选择变量，为提高回归方程精度和稳定性，增强回归方程预测的可靠性，需要对76个可供选择变量进行筛选，选择出对因变量贡献大的变量，从而建立最优回归方程。而利用逐步回归方法就可以实现这一目的，逐步回归是一种“有进有出”的分析方法，利用逐步回归可以理想的挑选出对因变量贡献大的变量，从而减少数据冗余，提高建模精度。该过程可在DPS平台下实现。

经分析当自变量数为7时，所建回归模型最好，所建方程中不存在对因变量影响不显著的变量，而且其相关系数和决定系数均较大，该回归方程为：

$\begin{array}{c}Y=22.415+39249.31X_1-13943.06X_2-24807.33X_3+296102.44X_4\\ -309086.89X_5+130909.69X_6-7751.45X_7\end{array}$ (2)

相关系数R = 0.9335，决定系数R² = 0.8715，F = 49.4128，P < 0.0001，Durbin-Watson = 2.0462。

方程中各X值含义及其偏相关性和p值见表2，

Table 2. Significance analysis of each coefficient

表2. 各系数的显著性分析

对回归模型的诊断主要涉及三个方面：一是方程的显著水平p必须小于等于0.05；二是各系数的偏相关系数的显著水平也要小于等于0.05；三是，Durbin-Watson统计量d是否接近于2。对此方程来说，方程的显著水平p < 0.0001，满足方程诊断的第一点要求，统计量d = 2.0462 ≈ 2同样满足上述要求。由表2可得，方程各系数的偏相关系数的显著水平均小于0.05，并且前6个系数的p值均达到0.0001，表明该模型回归极显著。

3.2.2. 基于主成分回归的叶绿素含量估测模型

主成分回归(Principal Component Regression, PCR)是一种减少数据集维数的回归分析方法，同时它能保持数据集的对方差贡献最大的特征，因此被广泛应用于数据分析和模型建立。

应用主成分回归建模时选取了两类数据，第一类是表1中的相关性绝对值最大值，第二类是利用逐步回回筛选出的7个变量。

根据特征值大于1的原则 [24] [25]，利用表1数据提取的主成分数为3，各主成分特征值及贡献率见表3。

Table 3. Principal component analysis of independent variables

表3. 自变量主成分分析表

表中3个主成分累计百分率达99.08%，代表了烟叶99.08%的信息。

主成分回归方程为：

$Y=17.645+4313.61{\left(\sqrt{R_{686}}\right)}^{\prime \text{}\prime }+276.24{\left(\sqrt{R_{705}}\right)}^{\prime }+3348.83\log {R^{″}}_{713}+174.03\log {R^{\prime }}_{703}+229.69{R^{\prime }}_{713}$ (3)

该模型中，由于 ${R^{″}}_{562}$ 中出现较多0值，故将 ${R^{″}}_{562}$ 剔除。

该方程中，F = 16.938，P < 0.0001，相关系数R = 0.693，决定系数R² = 0.480，Durbin-Watson = 2.222。

从以上数据可得，由各变换相关系数最大值组成的第一类数据所建模型预测效果并不理想。

采用第二类数据，即利用逐步回归筛选出的7个变量进行主成分回归分析。当累积方差贡献百分率达99%时，主成分个数为4，各主成分特征值及贡献率见表4。

Table 4. Principal component analysis of independent variables

表4. 自变量主成分分析表

由表4可以看出，表中4个自变量包含了烟叶99.66%的信息，完全可以代表整个烟叶信息。

根据主成分回归所得方程为：

$\begin{array}{c}Y=20.071+18.32X_1-313.41X_2+219.96X_3-5898.88X_4\\ -7582.90X_5+59389.72X_6+959.25X_7\end{array}$ (4)

相关系数R = 0.81158，决定系数R² = 0.6587，F = 20.7437，P < 0.0001，Durbin-Watson = 2.3346。各变量显著性分析见表5。

可以看出，变量b₀~b₆的p值都是0.0001，说明与因变量均是极显著相关，而b₇的p值虽然大于其他变量但也小于0.05，因此也与因变量显著相关。

比较回归方程(3)、(4)可以看出，利用逐步回归分析筛选出的变量所建立的主成分回归方程预测效果优于利用各变换相关系数最大值组成的变量所建模型。所以，首先采用逐步回归筛选出变量，再利用筛选出的变量建立模型可提高模型预测效果。比较回归方程(2)、(4)，方程(2)的决定系数R²和F值均大于方程(4)，并且(2)的统计量d更接近于2，因此，在该研究中基于逐步回归方法建立的模型优于基于主成分回归所建模型。

Table 5. Significance analysis of variables

表5. 各变量显著性分析

3.3. 估测模型检验

经以上分析，黑胫病烟草叶绿素含量预测最佳模型为：

$\begin{array}{c}Y=22.415+39249.31X_1-13943.06X_2-24807.33X_3+296102.44X_4\\ -309086.89X_5+130909.69X_6-7751.45X_7\end{array}$

式中，各X值如表2中所示。

模型精度主要是通过估测值与实测值的相关系数r和估测的误差均方根RMSE (Root Mean Square Error)来验证。利用第六个小区的60个数据对所建模型进行检验与测定，并作叶绿素实测值与估测值1:1关系图。

Figure 2. Monitoring and inspection results of chlorophyll content of Tobacco leaves influenced by Phytophthora parasitica var. nicotianae

图2. 黑胫病烟草叶片叶绿素含量监测检验结果

实测值与估测值之间的相关关系r = 0.8178，决定系数R² = 0.6887，RMSE = 1.97。

由图2可以看出，建立的黑胫病烟草叶绿素含量监测模型具有良好的拟合效果，决定系数R²达到 0.6887。表明模型对黑胫病烟草叶绿素含量具有较好的估测效果。

4. 结论

本研究分析了黑胫病烟草叶片原始光谱及其8种变换与叶绿素含量相关性，在此基础上运用逐步回归和主成分回归建立叶绿素含量估测模型，通过对比选出叶绿素含量最佳估测模型并对模型进行了检验。经分析研究主要得出以下结论：

1) 对光谱数据进行微分处理可以增加其信息量，对比原始光谱及其8种变换可以得出，原始光谱及各变换的一阶导数和二阶导数与叶绿素相关性都明显高于其原始形式；并且，各变换的一、二阶导数与叶绿素显著相关区域集中在450~750 nm之间。

2) 研究采用两类数据进行主成分回归，结果表明，先采用逐步回归筛选出变量，再利用筛选出的变量建立模型可提高模型预测效果。

3) 对比逐步回归模型和主成分回归模型可以得出，在本研究中，利用逐步回归方法所建模型预测效果优于主成分回归方法，最佳估测模型是以 ${\left(\sqrt{R_{706}}\right)}^{\prime }$ 、 ${\left(\sqrt{R_{702}}\right)}^{\prime }$ 、 ${\left(\sqrt{R_{710}}\right)}^{\prime }$ 、 $\log {R^{″}}_{712}$ 、 $\log {R^{″}}_{714}$ 、 ${R^{″}}_{562}$ 和 ${\left(\sqrt{R_{684}}\right)}^{\prime \text{}\prime }$ 为自变量，利用逐步回归方法所建，该模型的相关系数R为0.9935，决定系数R²为0.8715。经验证，该模型实测值与估测值的相关系数r为0.8178，决定系数为0.6887，说明利用逐步回归方法所建模型精度较好，可以反映黑胫病烟草叶绿素含量。

基金项目

国家自然科学基金(41171425)，山东省烟草公司重点项目( 2014-7-1 )，重庆市烟草公司重点项目(B20211NY1310)。

NOTES

^*通讯作者。