1. 引言
近年来,城市轨道交通行业高速发展,以地铁为代表的城市轨道交通已成为城市中重要的交通方式,因此轨道交通客流预测对于轨道建设、交通运营以及居民日常出行至关重要 [1]。
目前,众多学者针对不同场景下的客流提出不同的预测方法。孟品超等 [2] 采用滑动平均法对轨道交通短期客流进行实时预测,发现该方法处理速度快。朱霞等 [3] 从上海轨道交通运营线路的客流变化入手,探讨网络化进程对客流变化的影响,分析网络化进程中客流变化的原因。郑清杰 [4] 在分析历史新线接入后客流变化情况,基于土地利用性质对城市轨道交通车站进行K聚类,基于聚类结果及新线车站的评估,进行新线车站进出站量的预测。杨静等 [5] 提出一种基于变点模型、小波变换、自回归滑动平均模型的组合预测模型以此对某地铁站的进站量进行客流预测。
考虑到不同重要度等级下的站点客流特性有较大差异,时间序列模型的优势体现在能够更好地挖掘出数值变化背后的规律性。因此,本文基于苏州市城市轨道交通1号线2021年1月1日~2022年12月17日的日客流量数据,利用ARIMA模型预测与Prophet时间序列预测方法,对未来两周的日客流量进行预测。
2. ARIMA预测
ARIMA预测是时间序列预测中的一种,其根本是随着时间序列逐步呈现稳定化的时候,来预测模型因变量生成的推迟量、模型产生的不确定偏差后生成的推迟量和模型的当前量 [6]。模型是由三个部分集成得来的,分别包括名字中的AR、I、MA三个部分。
AR是模型中的自回归部分,因为该模型的预测方式与自身的变化有关,所以被叫作自回归模型,把模型中随着时间增减过程中数据自身生成的值作为模型数据取值,这样做的好处是能够不考虑除了自身环节外的其他环节的影响,坏处就是受自己本身环节的影响较大 [7]。把自回归模型阶数设置为模型的变量,并表示为变量p,变量p的意义就是运行时自回归模型采用的之前的时间断点间隔数量,p = 1代表此时模型会用到一个之前的时间断点数据,以此类推 [8]。其常见的表达式如下:
(1)
式中:
表示模型的预测量;
表示之前的时间断点数值;
表示之前的时间断点数值;
表示模型产生的偏差值;
表示一个常量;
表示之前时间断点的间隔数量。
I与AR不同,它不是一个单独的模型,它表示的是模型中的差分整合办法,数据的稳定化特征是这种方法的根本,对选择差分方法干扰最大的就是差分整合的基本数量,差分阶数一般表示为变量y。其一阶表达式如下:
(2)
二阶表达式如下:
(3)
式中:
表示差分整合数值;
表示之前的时间断点数据。
MA表示模型中的滑动平均数部分,为了减少或清除预测过程中能够生成的随机波动,通常预测基础选择的是自回归模型中的误差。模型中的变量一般是误差的阶数,用q表示。该模型的一般表达式如下:
(4)
式中:
表示之前的时间断点
上的偏差值;
表示偏差值增加权重后的系数;
表示一个常量。
将上述三个部分相互作用叠加可以得到一个新的模型,叫作自回归滑动平均数模型。自回归模型的阶数变量p与滑动平均数模型中的误差阶数变量q作为其变量 [9],通常这个模型表达式如下:
(5)
时间序列的平稳化是构建模型的前提,构建模型时可以使用差分法在时间序列展现相对稳定的形式时使时间序列趋于稳定化,将差分方法加入到式(5)中,并且按y阶差分的方法可以得到新的ARIMA模型。
3. Prophet预测
在应用时间序列预测的传统方法时,都需要将输入序列进行平滑处理,使序列稳定才能保证预测性能。而Prophet预测模型则不需要对源数据进行平滑处理,其最大的特点便是在预测模型中增添了增减趋势、季节趋势和节假趋势,其主体架构有似于广义加性模型(GAM) [10]。它的数学表达式可表示为:
(6)
其中,
、
、
和
分别表示为增减性趋势、季节性趋势、节假趋势和具有高斯分布特性的噪声。与ARIMA预测模型相比,其实践灵活性更高。
3.1. 增减趋势
增减趋势
是整个预测模型的核心,它表示的是整个时间序列是如何增减的,以及预期未来时间中的增减,其可表示为下式 [11]:
(7)
其中,C表示负载量,它的主要作用就是在拟合函数的过程中的函数无界,从而导致模型预测值过大而失效。
表示当前时间点的增长率,可正也可负。在Prophet预测模型中,额外添加了一个条件来保证预测记过不失真,并在关键时间节点出进行更改。
3.2. 季节性趋势
由于时间序列中可能包含多种周期类的季节性趋势,因此采用傅里叶技术来表示这个周期属性 [12],公式如下:
(8)
式中p是根据输入至模型的数据特性来表示周期的,如果采用传统认知的时间观点,那么p的取值就是7。N代表的是模型在迭代任务中提取周期的次数,如若N的值被错误的取小了,就会造成在拟合季节性分量时对p的依赖过高,从而导致模型的预测精度偏低。
3.3. 节假日趋势
在实际生活工作中,我们不难发现节假日或者是一些大事件左右人群的出行决策,会使时间序列的波动性陡然激增,特别是在轨道交通运营中,公休节假日前一天都会出现一波急剧增长的客流,而影响因素在短时的预测中不具备周期性特征,但对这些点的分析是不能忽略的,甚至得更加重视,有时候它的影响程度会远超常客流周期性的波动,例如在某站点图中有一个数据点激增,导致整体数据波动性增大 [13] [14]。综上节假趋势的表达式如下:
(9)
其中,
表示节假日对常数据影响的幅度,
表示节假日,
表示窗口长度。由于Prophet模型对输入数据的时间标签有一定的要求,故在实例分析时,本文将对数据的时间标签进行一定的修改,以此将Prophet模型应用到轨道交通预测中来。
4. 客流量预测结果分析
城市轨道交通的线路固定,受外界因素的干扰较小,居民使用轨道交通的时间周期性很强,所以整体的城市轨道交通客流量数据带有时序性特点,即客流量会随着时间点、季节、月份的变化而变化,但是最基本的是以周为单位的变化周期 [15]。
本文所采用的数据具体时间区间为2021年1月1日至2022年12月17日,在时间序列数据分析中,不同的时间区间会有不同的变化。因此,本文采用所选时间区间内的日客流量数据,分别利用ARIMA模型与Prophet模型进行后续14天的日客流量预测,并对预测模型的结果进行拟合,分析精度进行对比。自回归分析得到的实际日客流量的增减趋势如图1所示。
4.1. ARIMA预测结果分析
本文应用构建的模型ARIMA (1, 0, 14)对苏州市轨道交通一号线未来两周的线路日客流量进行预测分析。本文采用SPSS中的时间序列预测,首先对平稳时间序列分别求ACF自相关系数和PACF偏自相关系数,通过对图2中对ACF和PACF的分析,ARIMA模型进行定阶得到p和q的值,可见,绝大部分残差相关函数值均在95%置信区间内,即可说明模型通过检验,并由此建立ARIMA (1, 0, 14)模型。
ARIMA (1, 0, 14)模型对未来两周的线路日客流量预测结果可视化如图3所示。从图3中的时序图可以看出,模型的测试集拟合曲线和历史数据在部分时间点处有较高的拟合度,ARIMA (1, 0, 14)模型的预测值和客流量实际值的趋势变化较为同步,在有些时间点处的预测值和实际值之间的误差较小,但在某时间段内仍存在着较大的差值,拟合情况一般,说明ARMIA模型在处理非平稳序列时,表现较差,仅能对序列的基本趋势进行描述,无法满足轨道交通预测的高精度要求。
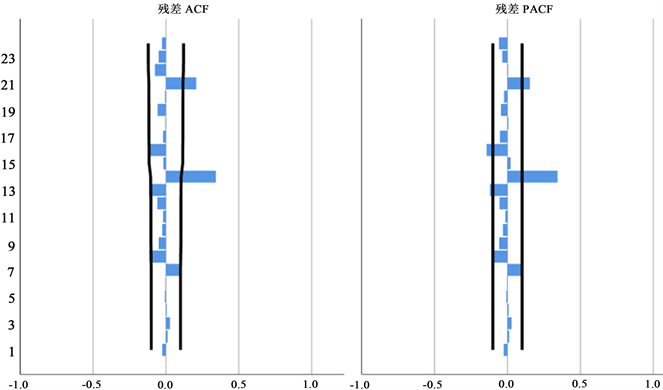
Figure 2. Autocorrelation and partial autocorrelation coefficient diagram
图2. 自相关和偏自相关系数图
4.2. Prophet预测结果分析
4.2.1. Prophet模型各组件的预测结果可视化分析
通过Prophet模型进行创建,并引入所选时间段内的客流量,得到如图4所示的城市轨道交通一号线客流量的非周期性变化趋势(具体的预测代码见附录)。可以看出,客流变化趋势是比较明显的,并没有明显的周期性。在2021年1月到10月客流量有着明显的下降趋势,说明这个时间区段内因受新冠疫情等因素造成客流量下降,10月以后的趋势出现明显的上升趋势,日客流量逐渐增大。
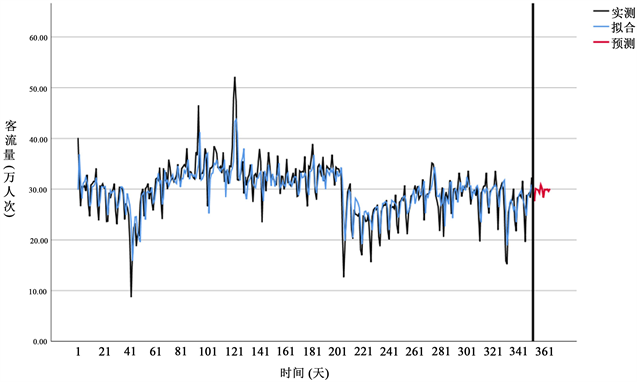
Figure 3. Fitting results of actual measurement and prediction
图3. 实测与预测拟合结果图
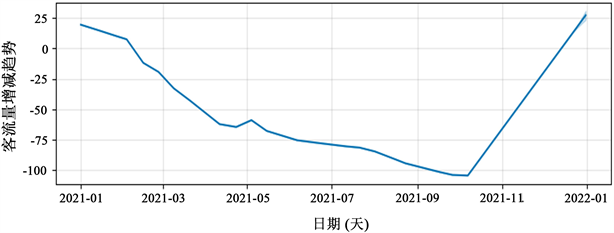
Figure 4. Non periodic trend of passenger flow
图4. 客流量的非周期性变化趋势
以周为单位的客流量季节性变化分别如图5所示。从图5中可以看出周日到周一以及周四到周五的客流量变化有明显的上升趋势,周一到周四期间的客流量变化趋于平稳,周五到周六的客流变化逐渐减弱,分析原因为在工作日选择乘坐地铁的人数较为稳定,周末休息日时日客流量波动较大,大多数人出行会选择乘坐地铁。
以年为单位的客流量季节性变化分别如图6所示。由图6可得,在1月至3月客流量变化有一个明显的上升趋势,因为这一时间段由国家传统节日“春节”,节日窗口前后的客流量波动较为明显,从三月至十月期间的趋势保持缓慢上升趋势,十月之后的客流量趋势减少。模型为了更好的拟合数据,通过对已知的突变点检测,使得季节性因素的影响作用显著增强。
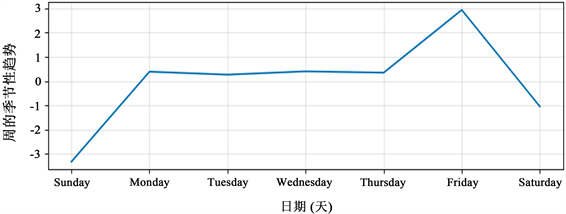
Figure 5. Seasonal change of passenger flow in weeks
图5. 以周为单位的客流量季节性变化
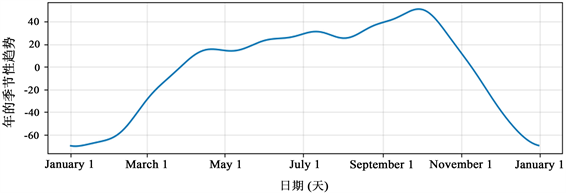
Figure 6. Seasonal change of passenger flow in year
图6. 以年为单位的客流量季节性变化
4.2.2. 客流量预测结果可视化分析
由于Prophet模型对时间序列整体的长度有一定的限制,且对于时间标签有着严格的要求,故采取两周的数据利用Python进行拟合预测,拟合情况如图7中Prophet模型拟合和预测结果所示。

Figure 7. Prophet model fitting and prediction results
图7. Prophet模型拟合和预测结果
图7中的横坐标为配合模型的输入而制作的从2021年1月1日至2021年12月31连续的时间标签,纵坐标即为客流量(万人次)。图中蓝色连续线为拟合后的数据,而离散的黑点为原始的苏州市地铁一号线的实际日客流量。预测的两周客流量结果为图中右边的最后部分(无黑点的部分),浅蓝色的区间为预测的置信上限与置信下限的范围。根据图7能够清晰地表现出模型拟合所选时段的日客流量规律,包括节假日以及季节性的变换规律。
4.3. 两种模型预测对比分析
通过ARIMA模型与Prophet模型的预测结果进行对比,可以清晰看出Prophet模型的优越性与准确性。根据两种模型的预测拟合情况可以发现,无论是采用哪种模型,都能够掌握基本的客流规律特征,并对未来一段时间的数据进行预测,但预测的精度却不同。本文分别选用R2、均方根误差(MSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)四个预测模型评价指标对ARIMA和Prophet模型的预测结果对比分析,结果如表1所示。

Table 1. Values of evaluation indexes of two models
表1. 两种模型评价指标的值
通过表2的结果对比显示,ARIMA预测相对误差小于0.1的有9天,大于0.1且小于0.2的有3天,大于0.2的有2天,最小相对误差为0.067,最大相对误差为0.3412,平均相对误差为0.1048。对于地铁日客流量的预测,从相对误差分析结果得到,ARIMA模型的预测结果在误差允许的范围内。Prophet模型预测结果相对误差小于0.1的有11天,大于0.1且小于0.2的有2天,大于0.2的有1天,相对误差值最小的为0.037,相对误差值最大的为0.2885,平均相对误差为0.0714。

Table 2. Comparison of passenger flow prediction results of two models
表2. 两种模型客流量预测结果对比
综合以上预测结果,根据预测拟合评价指标以及预测结果对比可以发现:
1) ARIMA作为一种最简单的传统时间序列模型来说从实际的客流规律来看,能勉强描述客流的大致趋势,仅仅拟合了以天为单位的具有相同特征的客流规律,对于某天因节假日等因素导致的大客流情况拟合的较差。
2) Prophet模型单从预测结果上来说,曲线更加平缓,客流预测的精度上于ARIMA相比较好,说明该模型适合长时间段的预测。
3) 两种模型的预测结果不同,其原因是由于不同单项模型对数据的敏感性不同,如ARIMA模型对时间序列中存在的线性趋势变化有较强的拟合分析能力,Prophet模型增加了对历史数据中节假日影响因子的有效分析,使得数据的预测分析更加接近于真实情况。由此可以看出,不同单项模型都有其各自的特点和局限性,因此单项模型的预测性能有待进一步提高。
5. 总结与展望
本文在对城市轨道交通客流预测模型进行系统分析的基础上,分别应用ARIMA模型和Prophet模型对城市轨道交通客流量进行拟合和预测,进而对两个模型预测的结果进行对比分析,从而评估模型预测的精度和性能。研究结果表明,首先结合ACF和PACF图进行模型的识别与定阶,利用SPSS进行时间序列预测得到最佳ARIMA预测模型。其次,Prophet模型是时间序列预测的一种新方法,其算法特点在于对历史数据中存在的节假日效应和季节效应的影响具有强敏感性,本文结合了Prophet算法这一特点构建了城市轨道交通客流量Prophet预测模型,最后通过对单项预测模型的预测结果进行了可视化分析并结合模型预测评价指标对两种模型之间的预测误差进行了综合对比分析。因此,针对日客流量的预测,Prophet模型的预测精度整体高于ARIMA模型,预测值与数据整体趋势大致相同,峰值存在误差,但整体偏差不大,结果表明需要优化或组合方法来提高预测的准确性。
基金项目
本文得到山东省自然科学基金项目(ZR2021MF109)和山东高速集团科技项目(2020-SDHS-GSJT-024)的联合支持。