基于BMA-QM的福建区域降水预报订正及暴雨检验研究

Precipitation Forecast Correction and Rain-storm Test in Fujian Province Based on Bayesian Model Averaging-Quantile Map-ping Method

摘要: 以全球交互式大集合预报系统提供的六种模式模拟的福建省及其周边区域2019年至2020年的4月至6月的日降水数据结果作为降水预报资料，以国家气象信息中心多源融合降水格点产品作为降水观测资料。对降水预报资料进行贝叶斯模型平均(简称BMA)方法订正后，对BMA方法订正结果使用分位数映射法(简称QM)进行再订正。结果表明：1) BMA方法订正后，提升模式在晴雨和小雨的预报技巧，但在中雨和大雨中未体现出优势。2) BMA-QM方法订正后，保持晴雨处的预报技巧之余，提升了小雨处的预报技巧，尤其提高了大雨处的预报技巧。3) BMA-QM方法订正之下，暴雨TS (0.163)和暴雨ETS (0.147)的提升率分别为98.30%、108.16%。BMA-QM方法订正可以提升模式对强降水的预报技巧，这将对做出更为准确的暴雨预警有着重要的意义。

Abstract: The 24-hour cumulative precipitation data from April to June in Fujian Province and its surround-ing areas from 2019 to 2020 simulated by six models provided by TIGGE are used as precipitation forecast data. The grid precipitation observation data are provided by CMPA. After the precipitation forecast data were revised by Bayesian model averaging, the results of BMA were revised using quantile-mapping. The results show as follows: 1) After BMA revision, the forecasting skills of mod-els in clear-rainy and light rain have been improved, but there is no improvement in moderate rain and heavy rain. 2) After BMA-QM revision, the forecasting skill of light rain, especially heavy rain, are improved while maintaining the forecasting skill of clear-rainy. 3) After BMA-QM revision, Thereat Score (0.163) and Equitable Threat Score (0.147) in rainstorm increased by 98.30% and 108.16% respectively. The correction of BMA-QM can improve the prediction skills of heavy precip-itation, which is of great significance to make more accurate rainstorm warning.

1. 引言

天气系统是一个混沌系统，天气预报无法达到百分之百的准确率，故在观测资料和模式模拟中都存在着不确定性 [1]。这些不确定性不利于获得准确的降水预报。集合预报的出现，促成天气预报从单一的数值预报走向概率性预报。Raftery等 [2] 在2005年将贝叶斯模型平均(Bayesian model averaging, BMA)引入气象领域的天气预报中，该法能量化概率性预报的不确定性。集合预报对比单一的确定性预报具有更高的研究价值，但是原始集合模式预报中也存在偏差，集合预报统计学后处理技术便应运而生 [3]。在Leamer [4] 给出BMA方法的框架之后，国内外学者开始探索如何将BMA方法延至多模式集合预报订正。

周梦瑶等 [5] 利用第五次耦合模式比较计划八个气候模式的预报资料来对赣江与汉江流域的降水和气温进行建模订正，结果表明在BMA方法订正后，都提高了模拟结果对气温和降水的精度，其中对气温订正效果的显著程度远比降水更高。吴裕珍等 [6] 利用了全球交互式大集合预报系统(THORPEX Interactive Grand Global Ensemble, TIGGE)收集的预报资料，研究东江流域降水概率预报，研究发现，BMA方法在降水量较小的情况下，改进了整个流域的各个时段中的预报效果。祁海霞等 [7] 将BMA方法应用于清江流域后，指出50%分位数预报对于一般降水的预报效果较好，而面对强降水、极端降水，确定性预报的分位点在50%~90%选取的效果更好。Javanshiri等 [8] 对比集合模型输出统计法和贝叶斯模型平均法的订正效果，可以发现经过后处理的集合预报均比未处理之前的预报结果更接近实况，且BMA方法更准确可靠。Sloughter等 [9] 证明，BMA方法对强降水事件订正的表现优于逻辑回归。周洁琴 [10] 指出BMA方法对轻降水事件预报准确，但是对中强降水的预报性能有限。

分位数映射法(Quantile-Mapping, QM)作为一种依赖频率分布来订正预报的方法，也是常用的统计学后处理技术。雷华锦等 [11] 将QM方法改进后应用于黑河上游区域的降水误差订正，发现订正后的预报数据在频率和降水量中都有明显的订正效果。包慧濛等 [12] 用频率匹配法对江西省欧洲中期气象预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)的降水预报进行偏差订正后降低了模式预报的小雨的空报率，以及大雨和暴雨量级中的漏报率，且订正后对于强降水的空间分布的形态和位置刻画效果较好。智协飞等 [13] 基于卡尔曼滤波法使用频率匹配法进行偏差订正后提升了各降水量级的ETS，对小于5毫米和大于15毫米的降水事件的预报技巧提升最为明显。Hamill等 [14] 选用QM方法进行偏差订正后不仅提高了预报技巧，也保持了降水分布的形态。喻雪晴等 [15] 对比研究了QM方法和比例缩放法，发现QM方法订正后的平均绝对百分比误差值最大值为2.31%，远比比例缩放法小。韩振宇等 [16] 对比前人的研究，指出QM方法能有效提高集合预报模式中的气温和降水的预报技巧。

福建省雨量充沛，气象灾害频发，精确的降水预报对该区域尤为重要，故本文选取福建省及其周边地区为研究区域，其中该区域的全年平均降雨量为1400至2000毫米之间 [17]。文中首先利用BMA方法对TIGGE数据集中六个模式日降水数据进行订正，并给出订正后的降水预报结果，分析BMA方法在不同降水分级中的订正效果。其次，对BMA方法订正后的结果使用QM方法进行再订正(记为BMA-QM)，以期提高预报在强降水处的预报技巧。BMA-QM方法订正或能提供更为准确的暴雨预警。

2. 资料与方法

2.1. 数据介绍

预报数据选取的是TIGGE提供的六个模式在福建省及其周边地区(23˚N~29˚N, 115˚E~121˚E)的日降水数据(1˚/day)。观测资料选取CMPA (China Merged Precipitation Analysis)降水融合资料(0.05˚/hourly)。降水资料信息如表1所见。时段为2019年至2020年的4月至6月。由于数据的空间分辨率不统一，采用双线性插值法统一分辨率为1˚ × 1˚。

Table 1. Precipitation data information

表1. 降水资料信息

2.2. 贝叶斯模型平均

贝叶斯模型平均(Bayesian model averaging, BMA)方法是一种基于贝叶斯理论的数据后处理方法，并能针对预报值得到具有预报效果的概率密度函数 [10]。

令 $f=f_1,\cdots ,f_k$ 分别表示K个不同数值模式预报结果，y为需要预报的变量， $y^{\text{T}}$ 为训练期数据。依据BMA原理，预报量y在训练数据下基于K个不同模式下的概率分布函数为：

$p\left(y|f_1,\cdots ,f_k\right)={\displaystyle \underset{k=1}{\overset{K}{\sum }}{w}_k{g}_k\left(y|\left(f_k,y^{\text{T}}\right)\right)}$ (1)

式中： $g_k\left(y|\left(f_k,y^{\text{T}}\right)\right)$ 为预报变量y在模型训练期阶段 $y^{\text{T}}$ 、模式 $f_k$ 预报为最佳预报条件下的概率密度函

数； $w_k$ 为各个集合模式在训练期为最佳预报的后验概率，也可称之为权重，非负且 ${\displaystyle \underset{k=1}{\overset{K}{\sum }}{w}_k}=1$，反映的是

每个数值模式在模型训练期对预报技巧的相对贡献程度。

类似降水数据这类不连续的变量，并不服从高斯分布。因此 $y|\left(f_k,y^{\text{T}}\right)$ 的分布可以分成两个部分来进行假设 [10]。

$g_k\left(y|\left(f_k,y^{\text{T}}\right)\right)=P\left(y=0|f_k\right)I\left[y=0\right]+P\left(y>0|f_k\right)g_k\left(y|\left(f_k,y^{\text{T}}\right)\right)I\left[y>0\right]$ (2)

其中，第一部分，无降水部分： $P\left(y=0|F^{M_i},Y\right)$ 是由逻辑回归模型得到的无降水概率。第二部分，有降水部分： $P\left(y>0|F^{M_i},Y\right)$ 为有降水概率， $y|F^{M_i}$ 服从伽马分布。

2.3. 分位数映射法

将降水事件通过不同的阈值划分成不同的等级后，在相同等级中，将预报的降水频率调整到和观测的降水频率一致，这就是频率匹配法 [13]。分位数映射法(Quantile-Mapping，QM)属于频率匹配法的一类，其认为观测降水和模拟降水在频率分布上是一致的 [11]。该方法通过建立模拟降水和观测降水之间的传递函数，对模拟降水进行订正。具体如下 [18]：

1) 计算CMPA降水数据和TIGGE提供的六种模式的降水预报数据的累积概率密度分布

2) 建立CMPA降水数据和各模式的降水预报数据的累积概率密度分布之间的传递函数

3) 利用传递函数对验证期的数据进行订正

$X_{cor}=F_{obs}^{-1}\left(F_{mod,train}\left(X_{mod,fut}\right)\right)$ (3)

其中， $F_{obs}$ 、 $F_{mod,train}$ 分别表示训练期内观测数据和模式数据的经验累积分布函数； $X_{mod,fut}$ 表示验证期(或者预测期，因为QM方法假设CMPA降水数据和各模式的降水预报数据的累积概率密度分布之间的传递函数在未来时期也不发生改变)； $X_{cor}$ 为验证期内模式的订正结果。

2.4. 预报效果检验方法

本文选取两种类型的指标对订正效果进行检验和评估，一类是统计指标，从数学的角度评价模型的效果；第二类是分级气象降水评价指标，从业务检验的角度来评估订正模型的效果。统计指标中选取平均绝对误差(Mean Absolute Error, MAE)和连续概率排位分数(Continuous Ranked Probability Score, CRPS)。平均绝对误差反映预报数据和观测数据之间的差距大小，连续等级概率评分是可以量化真实值和理论值之间的差异的指标。理想状态是 $\text{MAE}=0$， $\text{CRPS}=0$。两个指标的计算方式如下：

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|f{o}_i-o{b}_i\right|}$ (4)

$\text{CRPS}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{{\displaystyle \int \left[f\left(f{o}_i\right)-H\left(f{o}_i-o{b}_i\right)\right]}}^2\text{d}x}$ (5)

其中， $f{o}_i$ 和 $o{b}_i$ 分别代表的是第i个格点处的模式预报数据和观测数据， $f\left(f{o}_i\right)$ 表示概率预报累积分布函数； $H\left(f{o}_i-o{b}_i\right)$ 是Heaviside函数， $f{o}_i<o{b}_i$ 时为0，反之则为1；n是预报的总格点数。

业务上从降水分级角度对预报效果进行评估，降水分级则是按降水量为标准 [10] (如表2)。计算分级预报评价指标中，涉及到表3的混淆矩阵。表3中，NA、NB、NC、ND分别表示为命中个数、空报个数、漏报个数、反命中个数。技巧评分(Thereat Score, TS)是用以评价确定性预报的准确率的评分标准；公平技巧评分(Equitable ThreatScore，ETS)则在TS的基础上，考虑了空报和漏报的情况，并对这两种情况加以惩罚。偏差评分(Bias Score)是用以衡量模式预报与实况的预报偏差，可以用来体现降水总体的预报效果。理想预报状态下， $\text{TS}=1$， $\text{ETS}=1$， $\text{BIAS}=1$。各个指标的计算公式如下：

$TS=\frac{NA}{NA+NB+NC}$ (6)

$ETS=\frac{NA-R}{NA+NB+NC-R}$ (7)

$R=\frac{\left(NA+NB\right)\left(NA+NC\right)}{NA+NB+NC+ND}$ (8)

$BIAS=\frac{NA+NB}{NA+NC}$ (9)

Table 2. Classification table of precipitation grades

表2. 降水等级划分表

Table 3. Classification of predictive tests

表3. 预报检验分类表

3. 结果分析

3.1. BMA方法降水预报订正

3.1.1. 训练期选取

因为天气系统是一个无时无刻不在改变的系统，因此本文选择滑动建模。本文选取平均绝对误差(MAE)和连续概率排位分数(CRPS)作为指标来确定训练期长度。图1是不同训练期长度下福建及其周边地区BMA方法降水回报的MAE和CRPS趋势图，可见在94天的训练期之前，随着训练期长度的增加平均绝对误差和连续概率排位分数两个指标均出现了下降的趋势，并且在94天之后均趋于平稳。因此，确定训练期长度为94天。

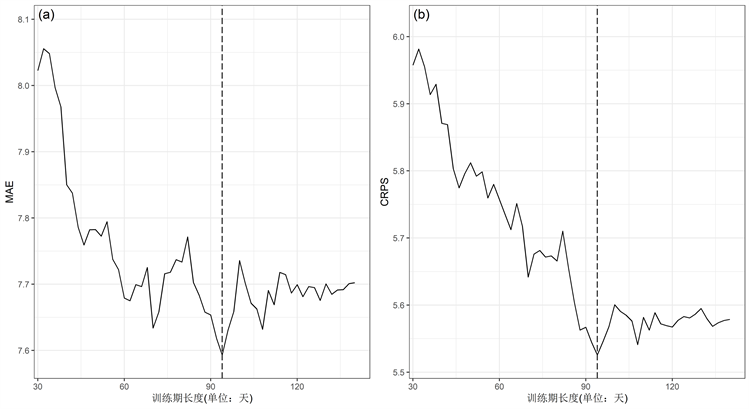
Figure 1. Index trend chart of precipitation return by BMA method in Fujian and its surrounding areas under different training periods (imaginary line is the position of 94 days): (a) MAE, (b) CRPS

图1. 不同训练期长度下福建及其周边地区BMA方法降水回报的指标趋势图(虚直线为94天所处位置)：(a) MAE指标，(b) CRPS指标

3.1.2. 各个集合模式的权重分布对比

根据BMA中各模式的权重随验证期内天数变化的折线图(图2(a))可以看到，各个模式的权重随时间变化而变化。这符合天气系统常常处于变化之中的现实情况。由BMA中各模式权重分布的箱线图(图2(b))可见，ECMWF和NCEP的权重的中位数分别是0.526和0.434，远远高于其他模式。即在建模过程中，ECMWF和NCEP对于订正效果的提升贡献较大。同时，通过评估各原始预报模式的预报技巧，确定原始最优模式为ECMWF，次优模式为NCEP。

3.1.3. BMA方法订正的降水预报结果评价

表4是BMA方法订正前后的分级降水预报评价指标对比，其中RAW表示加拿大气象局(ECCC)、欧洲中期天气预报中心(ECMWF)、日本气象厅(JMA)、韩国气象厅(KMA)、美国国家环境预测中心(NCEP)、英国气象局(UKMO)六个模式订正前的评价结果。由表4可得，经过BMA方法订正后，晴雨TS达到80.75%，对比ECMWF提升率达21.12%；在小雨处的TS提升率为35.49%。在各降水量级中，BMA方法订正后结果的ETS都比ECMWF更靠近1，即在ETS中体现出BMA模型在各降水量级的优势。经BMA方法订正后，结果在小雨量级处的BIAS评分更接近于1。

在三个指标的中强降水中，BMA方法订正后，TS和ETS次于ECMWF模式；BIAS评分仅优于NCEP模式。由此可得，经过BMA方法订正后，对比原始集合模式预报，在中雨和大雨以上量级中均出现了负技巧。这在一定程度上说明了BMA方法在小雨的订正效果明显，而在中强降水中预报能力有限。

同时通过对比不同指标的情况可以发现，相同的模型中，会出现指标的差异性，在之后分析也会从多角度出发。

Figure 2. Comparison of weight distribution of each set mode in the validation period: (a) Line chart of weight change of set mode, (b) Boxplot of weight distribution of set mode

图2. 验证期内各集合模式的权重分布对比：(a) 集合模式权重变化折线图，(b) 集合模式权重分布箱线图

Table 4. Comparison of evaluation indexes of graded precipitation forecast before and after the revision of BMA method

表4. BMA方法订正前后的分级降水预报评价指标对比

3.2. QM方法降水预报订正

本文对六个集合模式的降水预报使用QM方法订正，探讨QM方法在不同预报模式的订正效果差异，验证QM方法可以提升模式在小雨和大雨的预报技巧，而对于中雨的订正效果不如小雨和大雨这一结论的泛化性。

图3是QM方法订正前后的评分指标对比图。可见，除ECCC外的五个模式在QM方法之后的晴雨TS都出现了大幅度提升，并且整体在小雨TS有提升。NCEP的大雨TS的提升率甚至达32.15%，与此同时，ECMWF在大雨TS提升率也有3.6%。在各降水量级的ETS中，各模式的小雨ETS的订正效果最明显。除ECCC外的五个模式订正的小雨ETS均出现了提升，最低提升率超过30%，ECMWF模式的小雨ETS在QM订正后提升率高达264.72%，NCEP模式的小雨ETS提升率为289.70%。ECMWF模式和NCEP模式订正后的BIAS评分在各量级中表现均优，即在订正后表现出BIAS评分更接近1。在大雨BIAS评分中，改良效果最好的是ECMWF模式。改良效果最明显的是NCEP模式，ECMWF模式是改良效果次明显的模式。在QM方法订正后，NCEP模式|BIAS-1|的变化率达26.45%，ECMWF模式的变化率为8.39%。

改良效果的显著程度在不同的指标下不相同。对三个指标的趋势进行结合考虑后得出：其一，对预报性能越好的预报模式数据进行QM订正后的订正效果越显著；其二，对模式数据进行QM方法订正后，订正效果的显著程度随量级的增大而减小；其三，QM方法在小雨和大雨量级处的订正效果优于中雨量级。

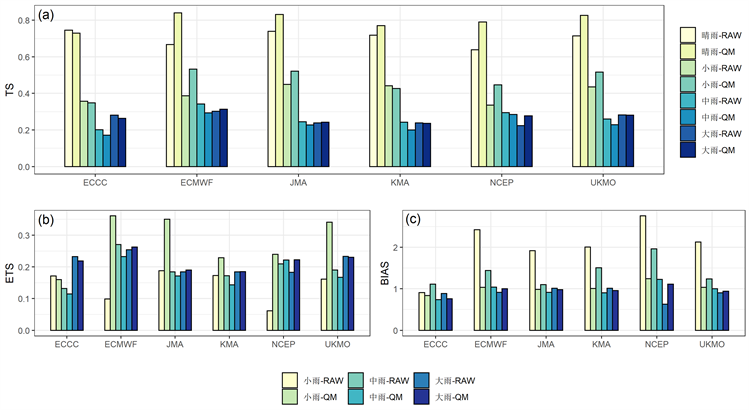
Figure 3. Comparison of scoring indexes before and after QM revision: (a) TS, (b) ETS, (c) BIAS

图3. QM订正前后的评分指标对比: (a) TS, (b) ETS, (c) BIAS评分

3.3. BMA-QM降水预报订正

由前文可得，BMA方法订正后的模式数据在中雨以上量级都出现了预报负技巧，QM方法具有改善预报中存在“小雨空报，大雨漏报”问题的能力。为此本节将结合BMA方法对中强降水预报技巧提升有限的情况，对BMA方法订正后的结果使用QM方法进行再订正。

3.3.1. BMA-QM方法订正的降水预报结果评价

图4是BMA和BMA-QM方法订正前后评分指标对比图。对比BMA方法订正，BMA-QM方法订正后在晴雨TS、小雨TS和大雨TS的提升率分别为3.62%、3.08%和8.63%，在小雨ETS和大雨ETS的提升率分别为16.63%和4.62%。对比ECMWF模式，BMA-QM方法订正后在小雨TS和大雨TS提升率分别为39.67%和5.69%，在小雨ETS和大雨ETS提升率分别为85.25%和4.97%。经BMA方法订正的和BMA-QM方法订正的结果在各降水量级BIAS评分中，均体现出BMA-QM方法的优势，这与前文QM方法在BIAS评分下的效果一致，即ECMWF模式在各量级BIAS评分都体现出改良效果。ECMWF模式的大雨BIAS评分为0.916，即存在漏报的情况。在进行BMA-QM方法订正之后，BIAS评分从BMA方法订正的0.645提升至1.103。

在BIAS评分中，BMA-QM方法订正后，提升了模式预报对于中雨事件的预报技巧。然而，BMA方法订正和BMA-QM方法订正后，在TS和ETS指标中，未表现出对中雨降水事件的订正技巧提高。结合三个指标说明，对中雨事件的预报订正中，减轻了空报情况的同时，加剧了漏报和不能命中预报的情况。

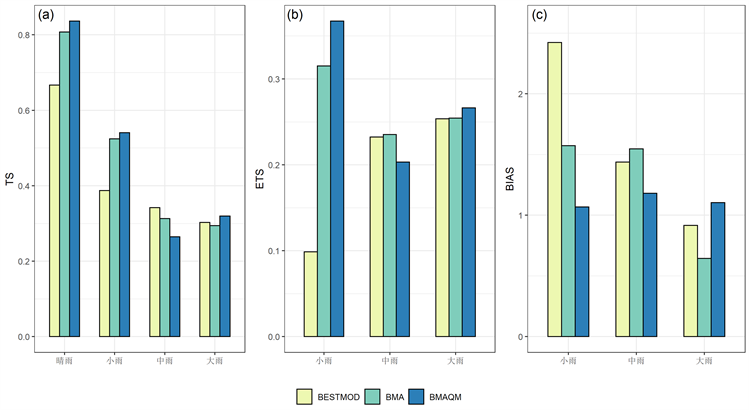
Figure 4. Comparison of scoring indexes before and after BMA revision and BMA-QM revision: (a) TS, (b) ETS, (c) BIAS

图4. BMA方法订正和BMA-QM方法订正前后评分指标对比：(a) TS，(b) ETS，(c) BIAS评分

3.3.2. BMA-QM方法订正的暴雨检验评分

结合前文，本文给出BMA-QM方法订正后全区域的暴雨检验评分。表5是BMA方法订正和BMA-QM方法订正前后的暴雨检验评分对比，其中BESTMOD、BMA、BMA-QM分别代表ECMWF模式的数据、BMA方法订正后的结果、BMA-QM方法订正后的结果对应的暴雨检验评分。经BMA-QM方法订正后，暴雨TS对比ECMWF模式提升率达98.30%，暴雨ETS的提升率达108.16%。基于ECMWF模式和BMA方法订正的暴雨BIAS评分都小于1的情况来看，BMA-QM方法订正后暴雨BIAS评分大于1。出现这样的结果，是因为在调节降水强度的过程中，减少了漏报的同时也增加了空报，而空报增加的幅度远低于漏报减少的幅度，同时，预报命中情况从好到差的顺序为BMA-QM方法订正后的结果、ECMWF模式数据、BMA方法订正后的结果。这导致了BMA-QM的最终结果在暴雨量级中的TS和ETS表现良好，但BIAS评分表现不佳。总体而言，BMA-QM方法订正对暴雨的预报技巧的提升明显。

Table 5. Comparison of rainstorm test scores before and after BMA revision and BMA-QM rerevision

表5. BMA方法订正和BMA-QM方法订正前后的暴雨检验评分对比

3.3.3. 2020年6月5日降水订正的个例分析

由图5的2020年6月5日日降水情况对比图可见，ECMWF模式能较好的刻画出该地区的降水重心，尤其是研究区域的西北部，但ECMWF模式并没有将研究区域在东南部的无雨带刻画出来。BMA方法订正后，将这个区域的无雨带及主雨带的位置和形态刻画出来。BMA-QM方法订正之后，将主雨带的形态、位置、强度刻画相对完整。BMA方法订正以及BMA-QM方法订正之后主雨带的形态和位置几乎相似，且在无雨部分，BMA-QM更接近实况。

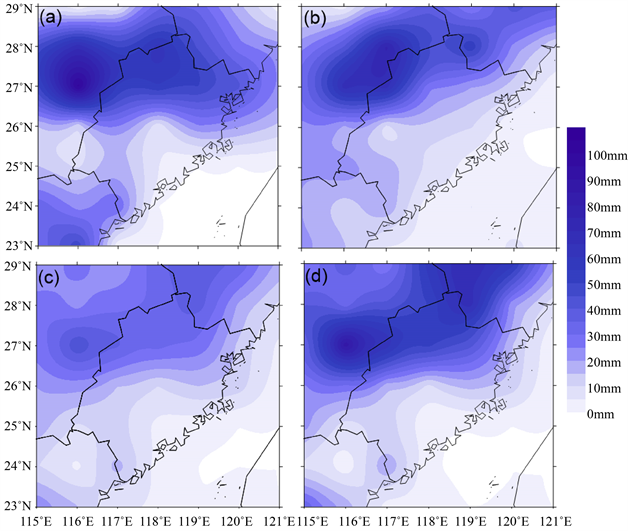
Figure 5. Comparison of cumulative precipitation in 24 hours on June 5, 2020 (unit: mm): (a) Observation, (b) Original optimal forecast model, (c) Deterministic precipitation forecast after BMA correction, (d) Deterministic precipitation forecast after BMA-QM revision

图5. 2020年6月5日24小时累积降水情况对比(单位：mm)：(a) 观测，(b) 原始最优预报模式，(c) BMA方法订正后降水预报，(d) BMA-QM方法订正后降水预报

通过计算指标，BMA-QM方法对比BMA方法在平均绝对误差的订正率为4.95%，对比ECMWF模式平均绝对误差的订正率为4.37%。由图6的2020年6月5日降水预报各个指标对比图，可以看出BMA-QM方法订正后的TS和ETS在三个量级都比BMA方法订正之下的情况更好。在BIAS评分中，小雨和大雨量级里，BMA-QM方法订正均改善了空报的情况，而在中雨量级中，BMA方法订正已经达到理想预报的状态，此时BMA-QM并没有保持中雨的BIAS评分，甚至还比ECMWF模式还差。说明在该订正个例的降水过程中，BMA-QM方法订正后的中雨量级里的空报，对比BMA方法订正和ECMWF模式更严重。出现这样的情况是因为BMA-QM方法订正的过程中，在大雨量级的降水强度调高的同时，接近中雨的小雨处对应的预报降水强度也提高了，最终导致中雨量级空报增加。

总体而言，在此次降水过程中，BMA-QM方法订正后，不仅保持了晴雨量级下的预报技巧，也提升了小雨处的预报技巧，尤其是提高了中雨和大雨量级的预报技巧。这也验证了前文的分析结论。

Figure 6. Comparison of precipitation forecast indicators for June 5, 2020: (a) TS, (b) ETS, (c) BIAS

图6. 2020年6月5日降水预报各个指标对比：(a) TS，(b) ETS，(c) BIAS评分

4. 结论

本文使用福建省及其周边地区在2019年至2020年4月~6月的日降水资料以及6个集合预报模式的日降水数据，利用BMA方法对六个集合预报模式的降水数据进行订正后，利用QM方法对经BMA方法订正后的结果进行再订正。选取2020年5月28日~2020年6月26日作为验证期，得到以下的主要结论：

1) BMA方法订正后，在晴雨和小雨处的订正效果最明显，但BMA方法订正后在TS和BIAS评分中并没有在中强降水上表现出订正优势。BMA方法订正后的结果在ETS指标中，对比ECMWF模式在中强降水上有改良效果。说明在不同的指标中，订正效果的显著程度不相同。

2) 在对六个原始模式分别进行QM方法订正后发现，TS、ETS、BIAS评分均表明QM方法在ECMWF和NCEP这两个模式的订正较好。并且也验证了QM方法在小雨和大雨，对比中雨有更好的订正效果。

3) BMA-QM方法订正之后，其结果在各级BIAS评分中对比ECMWF模式均有改进。对比ECMWF模式，BMA-QM方法订正后的晴雨、小雨和大雨的TS提升率分别为25.5%、39.67%和5.69%；小雨和大雨的ETS的提升率分别为85.25%和4.97%。同时，BMA方法订正和BMA-QM方法订正的结果对应的中雨TS分别为31.33%、26.47%，中雨ETS分别为23.52%、20.31%，对比ECMWF模式(中雨TS：34.17%、中雨ETS：23.25%)，BMA方法订正和BMA-QM方法订正的结果均未表现出对中雨事件订正技巧提高，且BMA-QM方法订正的结果对比BMA方法订正结果出现了更明显的负技巧。

4) 对研究区域进行暴雨检验后发现：BMA-QM方法订正后的结果对比ECMWF模式的数据，暴雨TS和暴雨ETS提升率分别高达98.30%和108.16%。BIAS评分不减反增之因或在，调节降水强度时，为保实况资料和BMA方法订正后的结果两者累积概率密度分布一致，不免将实况中大雨降水事件调至暴雨事件，便增加了空报。个例分析表明：经BMA-QM方法订正后，不仅保持了晴雨处的预报技巧，提升小雨处的预报技巧，也提高了中雨量级和大雨量级的预报技巧。BMA-QM方法订正后的结果在中雨量级里，空报对比BMA订正和ECMWF模式更严重。

致谢

本论文的顺利完成离不开导师的指导和林青和潘宁两位福建省气象台的专家提供的数据，向三位老师表示衷心感谢。同时，也向帮助和关心过我的同门表示感谢。

基金项目

江苏省研究生科研实践项目(SJCX21_0374)。