基于多线激光雷达的地图构建技术研究

Research on Map Construction Technology Based on Multi-line Li DAR

摘要: 基于激光雷达的三维点云地图构建过程中点云配准是一个重要的研究部分，目前点云配准主要采用传统迭代最近点算法(ICP)。由于传统迭代最近点算法使用点到点的配准方式，导致点云配准耗时长，容易产生误差造成点云配准精度低的问题。针对上述问题，本文在基于传统迭代最近点算法原理上结合Point-to-Line ICP (PL-ICP)算法与Point-to-Plane ICP (PP-ICP)算法提出了一种对ICP算法改良的方案。在点云帧间配准中，将寻找对应点集的配准方式改为点到线和点到面的方式进行点云配准，实验结果表明，本文提出的方法能够有效构建点云地图，减少了点云配准时间，具有良好的配准精度。

Abstract: Point cloud registration is an important part of 3D point cloud map construction based on mul-ti-linelidar. At present, traditional iterative nearest point algorithm (ICP) is mainly used for point cloud registration. For the traditional iterative nearest point algorithm, point cloud registration is time-consuming and error-prone, which leads to the low accuracy of point cloud registration. Based on the principle of traditional iterative nearest point algorithm, this paper proposes an improved ICP algorithm combining PL-ICP algorithm and PP-ICP algorithm. In the point cloud inter-frame registration, the registration method of finding the corresponding point set is changed to the point-to-line and point-to-surface methods for point cloud registration. The experimental results show that the method proposed in this paper can effectively construct a point cloud map. The point cloud registration time is reduced and the registration accuracy is good.

1. 引言

近些年随着科技的发展进步，无人驾驶 [1] [2] [3] 越来越受到人们的关注。同时定位与建图(SLAM) [4] [5]，在无人驾驶领域可以理解为无人车从一个未知的位置开始运动并于运动过程中构建地图。目前点云匹配技术 [6] [7] 已经发展的比较成熟，由Besl和McKay提出的迭代最近点算法(ICP) [8] 是目前在应用建图中最为经典的算法。它的主要思路是在获取到源点云和目标点云后，通过欧式距离最近策略不断的迭代调整源点云的位姿，使得源点云和目标点云在同一坐标系，最终使得源点云和目标点云误差累积最小化，进而获取激光雷达的运动估计。但是由于传统的ICP算法使用点到点的配准方式 [9]，导致点云配准耗时长，容易产生误差造成点云配准精度低。针对这些问题，Censi A等人 [10] 提出的ICP变种算法PL-ICP和Pathak K [11] 提出的PP-ICP算法，都改进了对应点集的选取方式，效率得到提高，但相较于ICP算法对初值更敏感，需要从大量的激光雷达中提取特征点。近年来也有学者提出将多个匹配算法相结合 [12] 的方案，如：2020年姜祚鹏等人 [13] 提出了一种基于PL-ICP和NDT的点云匹配算法，该算法是基于二维的单线激光雷达 [14] 来实现建图，在一些较小场景下效果较好，缺点是对于使用三维的多线激光雷达采集较大场景的点云数据建图，建图精度较差。

基于以上研究，本文根据传统迭代最近点算法(ICP)原理结合PL-ICP算法与PP-ICP算法，基于多线激光雷达提出了一种对ICP算法改进的方案。首先对点云进行预处理，主要对原始点云进行降采样和特征点提取，提取的点云分为边缘点集点云和平面点集点云。在点云帧间配准中，将传统ICP算法点到点寻找对应点集的配准方式改为点到线和点到面的方式进行点云配准。该方法能够有效避免传统迭代最近点算法对点云配准耗时长和容易产生误差造成点云配准精度低的问题。

2. 迭代最近点算法

假设得到两片源点云集合 $P=\left\{p_1,p_2,\cdots ,p_N\right\}$ 和目标点云集合 $X=\left\{x_1,x_2,\cdots ,x_N\right\}$，经典ICP算法使用的点到点的对应关系如公式1所示：

$d=\min \Vert X-{\left(R\ast P+t\right)}^2\Vert$ (1)

式(1)中R和t分别是源点云集P到目标点云集X的旋转矩阵和平移矩阵，d为两个对应点云的最小欧氏距离，迭代最近点算法(Iterated Closest Points, ICP) [15] 的流程如下：

1) 初始化过程：

a) 设置最大迭代次数 $j_{\max }$ 和误差的阈值φ。

b) 分别初始化旋转矩阵R和平移矩阵t，R为单位矩阵、t为零向量。

2) 迭代过程：

a) 通过遍历当前源点云集P的每个点的欧式距离，找到与目标点云X匹配的对应点对。

b) 通过找到对应点的约束关系，构造两帧点云间的误差函数： ${\min }_{R,t}=\frac{1}{S_p}{\displaystyle {\sum }_{i=1}^{S_p}{\Vert x_i-\left(R{p}_i+t\right)\Vert }^2}$，计

算旋转矩阵R和平移矩阵t。 $S_p$ 代表当前源点云集P的点云数，R、t构成位姿变换矩阵记为T。

c) 判断当前的迭代次数是否达到最大迭代次数 $j_{\max }$ 或者位姿变换矩阵T的变化量是否满足误差阈值φ的条件，如果满足的话，停止迭代；若没有达到满足条件，则重新开始进行再次迭代。

该算法的问题在于使用点到点的方式寻找对应点集，容易找到错误的对应点产生误差造成点云配准精度低的情况，从而造成配准粗糙。ICP变种算法PL-ICP和PP-ICP算法，都是基于传统ICP算法的原理进行的改良。两种算法都改进了对应点集的选取方式，PL-ICP是点到线的方式寻找对应点集，效率得到提高，但相较于ICP算法对初值更敏感。PP-ICP是点到面的方式寻找对应点集，效率更高，但需要从大量的激光雷达中提取特征点。为减少误差的产生，计算出来的点云变换是精确的，本文结合这两种算法对传统ICP算法进行改进。

3. 改进的迭代最近点算法

3.1. 点云预处理

对于多线激光雷达，在获得原始的点云数据过程中，每秒的点云数据量高达几十万，十分巨大。如果直接使用原始的点云数据，在点云匹配等一些处理中，点云数据量巨大使得算法的时间复杂度非常高，同时误差的累计使得算法的运行效果不良。因此在后期应用需要对原始的点云数据进行预处理，本文主要对原始点云进行降采样。建图是一个增量式的实时建图过程 [16] [17]，需要存储大量的点云数据而且密集，故此需要在不丢失点云数据的环境表征能力的前提之下使用降采样法，本文采用体素网格滤波器的方法来对原始点云进行降采样。

体素网格滤波的实现原理是：首先将输入的三维点云表示的空间划分为一个个边长相等的三维体素网格，然后在每个体素网格中选择一个点来近似代替所有存在的点，使用每个体素网格的质心作为近似值，其质心的坐标 $\left(x_c,y_c,z_c\right)$ 如公式(2)所示：

$x_c=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{x}_i},y_c=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{y}_i},z_c=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{z}_i}.$ (2)

体素内总共有N个点云，每个点云用 $p_i=\left(x_i,y_i,z_i\right)$ 表示。本文采用PCL实现的VoxelGrid类，图1显示了使用体素网格滤波器的方法，原始点云滤波前后的对比结果。可以看出在保证点云的原始形状特征和空间结构信息基本不变的情况下，一定程度上降低了点云的密度与数量。

Figure 1. Comparison of point clouds before and after voxel grid filtering

图1. 体素网格滤波前后点云对比图

3.2. 特征点提取

为了计算激光雷达的运动位姿，需要得到的是相邻帧间的姿态变换关系。在相邻帧间点云配准中，若直接将相邻两帧之间的点云进行匹配，计算量巨大，是不可靠的。为了减少计算的时间消耗，使用特征点来代替完整的数据帧，本文根据点的曲率来计算平面光滑度作为提取当前帧的特征信息的指标。平滑度公式如下：

$\text{C}=\frac{1}{s\ast \left|M_i^L\right|}\ast \left|{\displaystyle {\sum }_{j\in s,j\ne i}\left(M_i^L-M_j^L\right)}\right|\text{.}$ (3)

公式(3)中，i是某一帧点云数据中的一个点， $M_i^L$ 表示激光雷达坐标系{L}下的坐标，s表示计算平滑度点的数量。

计算每个点对应的c值，根据c值的大小来确定特征点，某点对应的平面光滑度越大，表明该点在其所在的局部曲面上越尖锐，当某点的平面光滑度超过一定阈值时，该点可以定义为边缘点；相反，如果某点对应的平面光滑度较小，则表明该点在其所在的局部曲面中更平滑，当某点的平面光滑度低于某个阈值时，可以将该点定义为平面点。因此根据平面光滑度大小可以将特征点划分为两大类：平面特征点和边缘特征点。本文特征点提取的主要思路为：

1) 为了保证提取的特征点均匀分布，将激光点云按照激光雷达线束的形式排列，将每一条线束均匀分成各小段，再在每一段中遍历每个点计算c值。

2) 根据c值的大小，将每段截面中的点从大到小排序，然后选择平滑度最大的两个点，判断其值是否大于边缘特征点的设定阈值。如果大于，则它们将用作边缘特征点。然后判断平滑度最低的四个点的值是否小于面特征点的设定阈值。如果小于，则将其视为平面特征点。

3) 最后，提取的边缘特征点和平面特征点分别构成边缘特征点集和平面特征点集。因此，该方法可以获得当前帧的点云数据对应的特征点信息。

3.3. 帧间匹配

特征点提取之后，需要将两帧特征点数据进行匹配 [18]。本文的帧间匹配算法是在传统ICP算法的基础上进行的改良，针对寻找对应点的方式提出了一种结合点到线的ICP算法和点到面的ICP算法的配准方式。在前面特征点提取部分已经得到了边缘特征点集合和平面特征点集合，然后通过提出的算法，对获得的边缘特征点集和平面特征点集分别进行边缘特征点匹配和平面特征点匹配，把寻找对应点改为寻找对应线和对应面。通过该方法可以使得点云配准有针对性，提高点云配准精度。

3.3.1. 边缘特征点匹配

如图2所示，图中p点是当前帧的边缘特征点，q点是上一帧边缘点集合中离p点距离最近的点，r点是上一帧q点的邻近点，p点是上一帧qr形成的“折线”中的某点在当前帧被提取，所以p点到qr的距离表示了当前帧和上一帧的运动关系。

用坐标的形式把图2中的点来表示，设p点的坐标为 $\left(x_p,y_p,z_p\right)$，q点的坐标为 $\left(x_q,y_q,z_q\right)$，r点的坐标为 $\left(x_r,y_r,z_r\right)$，则向量 $a$ 可表示为 $\left(x_p,y_p,z_p\right)-\left(x_q,y_q,z_q\right)$，向量 $b$ 可表示为 $\left(x_q,y_q,z_q\right)-\left(x_r,y_r,z_r\right)$，向量 $c$ 可表示为 $\left(x_p,y_p,z_p\right)-\left(x_r,y_r,z_r\right)$。由于向量积在数值上等于向量 $a$， $c$，夹角 $\theta$ 组成的平行四边形的面积，可以得出 $S_{pqnr}=S_{pqrm}=\left|a\right|\ast \left|c\right|\ast \sin \theta =S_{oqrt}=\left|b\right|\ast d$，由此可以推导出点p到直线qr的距离为：

$d=\frac{\left|a\ast c\right|}{\left|b\right|}$ (4)

若是用点坐标来表示，则式(4)可以表示为：

$d=\frac{\left|\left\{\left(x_p,y_p,z_p\right)-\left(x_q,y_q,z_q\right)\right\}\ast \left\{\left(x_p,y_p,z_p\right)-\left(x_r,y_r,z_r\right)\right\}\right|}{\left|\left(x_q,y_q,z_q\right)-\left(x_r,y_r,z_r\right)\right|}$ (5)

式(5)表示了p点到qr的距离即当前帧的边缘特征点与上一帧对应的边缘特征点之间的运动关系。

Figure 2. Geometric relationship between point and line distance

图2. 点到直线距离的几何关系

3.3.2. 平面特征点匹配

如图3所示，图中p点是当前帧的平面特征点，q点是上一帧平面点集合中离p点最近的点，在最近邻点q点所在线束再寻找另外一个最近点m点，以及在最近邻点q点所在线束的相邻线束中寻找第三个最近点r点，m和r点都是上一帧q点的邻近点，这个三点组成匹配平面。p点是上一帧qmr形成的“平面”中的某一点在当前帧被提取，所以p点到qmr平面的距离表示了上一帧和当前帧的运动关系。

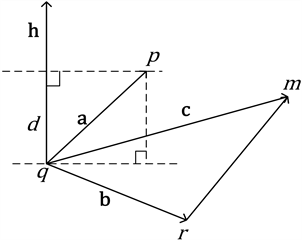
Figure 3. Geometric relationship between point and plane distance

图3. 点到平面距离的几何关系

用坐标的形式表示图3中的点，设p点的坐标为 $\left(x_p,y_p,z_p\right)$，q点的坐标为 $\left(x_q,y_q,z_q\right)$，r点的坐标为 $\left(x_r,y_r,z_r\right)$，m点的坐标为 $\left(x_m,y_m,z_m\right)$。用坐标的形式表示向量 $a$ 可表为 $\left(x_q,y_q,z_q\right)-\left(x_p,y_p,z_p\right)$，向量 $b$ 可表为 $\left(x_q,y_q,z_q\right)-\left(x_r,y_r,z_r\right)$，向量 $c$ 可为 $\left(x_q,y_q,z_q\right)-\left(x_m,y_m,z_m\right)$。d可以用来表示p点到qmr三点形成的平面的距离，而向量 $a$ 在向量 $h$ 上的投影也可以用d来表示。所以d可表示为：

$d=\frac{\left|a\ast h\right|}{\left|h\right|}$ (6)

由向量积知 $\left|h\right|=\left|b\times c\right|$，所以d表示为：

$d=\frac{\left|a\ast \left(b\times c\right)\right|}{\left|b\times c\right|}$ (7)

若是用坐标来表示，则式(7)可以表示为：

$d=\frac{\left|\left\{\left(x_q,y_q,z_q\right)-\left(x_p,y_p,z_p\right)\right\}\ast \left\{\left\{\left(x_q,y_q,z_q\right)-\left(x_r,y_r,z_r\right)\right\}\times \left\{\left(x_q,y_q,z_q\right)-\left(x_m,y_m,z_m\right)\right\}\right\}\right|}{\left|\left\{\left(x_q,y_q,z_q\right)-\left(x_r,y_r,z_r\right)\right\}\times \left\{\left(x_q,y_q,z_q\right)-\left(x_m,y_m,z_m\right)\right\}\right|}$ (8)

式(8)则表示了p点到qmr三点形成的平面的距离即当前帧的平面特征点与上一帧对应的平面特征点之间的约束方程。

本节通过计算边缘特征点到对应直线的距离和平面特征点到对应面的距离，推导出特征点云和与之匹配的点云之间的运动变化量作为最终的误差函数。采用非线性优化算法(高斯牛顿法或列文伯格–马夸尔特法)更新变化矩阵，最小化误差函数。当迭代次数达到最大迭代次数或者位姿变换矩阵的变化量满足误差阈值的条件时，停止迭代，从而完成帧间运动估计。然后通过增量式地图构建，可以创建出完整的全局点云地图。

4. 实验与分析

实验所用到的计算机主要配置为Intel(R) Core(TM) i5-10200H 2.40 GHz CPU，16GB内存，英伟达RTX2080显卡，操作系统为Ubuntu 16.04下kinetic版本的ROS系统。本文从点云配准精度和点云配准耗时的角度来设计实验，将该算法与其他配准算法进行比较分析。以下实验分两部分进行：Mulran数据集点云配准效果和精度对比、配准算法的配准用时比较。

4.1. Mulran数据集点云配准效果和精度对比

本实验所需要的点云数据来自于Mulran数据集下的KAIST02激光雷达数据。该数据集包含市区高层建筑之间的道路、园区封闭环境以及河流和桥梁等场景的点云数据，是目前自动驾驶领域应用最广泛的算法评估数据集，本实验采用数据集中KAIST02园区场景的部分点云数据。在该场景下对点云配准效果进行验证比较，首先是对原始点云降采样，然后运用本文算法来进行实验，结果如图4所示，图4(a)为两帧未配准的点云，蓝色为源点云，红色为目标点云。点云配准精度对比结果如表1所示。

(a) 未配准 (b) NDT算法 (c) 传统ICP算法 (c) PP-ICP算法 (d) PL-ICP算法 (e) 本文算法

Figure 4. Park scene point cloud registration effect

图4. 园区场景点云配准效果

Table 1. Comparison of registration accuracy of each algorithm in park point cloud scene

表1. 园区点云场景下各个算法配准精度比较

4.2. 配准用时比较

本实验从Mulran数据集中截取3000帧点云数据来进行各个配准算法的帧间配准用时对比，图5为各个配准算法的各帧配准用时效果图，表2为各个配准算法的配准结果的数据。

Figure 5. Frame registration time

图5. 各帧配准用时

Table 2. Comparison of registration time of each registration algorithm

表2. 各个配准算法的配准用时比较

4.3. 实验结果分析

结合以上点云配准效果和帧间配准用时实验数据对比分析可知，NDT配准算法虽然时间上面耗时最短，但是其点云配准容易产生误差，点云配准效果不理想。传统ICP算法采用点到点的对应方式，对点云进行配准耗时长，容易陷入局部最优导致点云配准精度低。PP-ICP配准算法和PL-ICP配准算法都是在传统ICP算法的基础上进行的改良，改进了对应点集的选取方式。PL-ICP是点到线的选取方式，PL-ICP算法误差函数为点到线的距离优点是点云配准精度提高，但和PP-ICP算法与本文算法相比较其点云配准时间耗时比较长。PP-ICP是点到面的选取方式，其优点是点云配准时间耗时少，缺点是点云配准精度不理想。本文算法使用点到线和点到面相结合的方式进行点云配准，在点云配准效果上都优于以上算法，配准效率也比较良好满足需求。通过以上实验对比分析，我们得出本文算法更适合基于多线激光雷达的地图构建。

5. 点云建图结果

使用Mulran数据集采用本文算法来构建完整的地图效果如下：

图6(a)为该区域的全局俯视图，可以看出这是一个园区闭环地图。图6(b)为整体的全局侧视图，图6(c)和图6(d)为该区域局部不同放大程度的细节图。从这两幅详图中，可以清楚地看到场景中建筑物、停放车辆和其他物体的轮廓，道路两侧的树木清晰，具有很高的真实性。

(a) 全局俯视图 (b) 全局侧视图 (c) 细节图1 (d) 细节图2

Figure 6. Closed-loop area mapping effect

图6. 闭环区域建图效果

6. 结语

本文对获取的点云进行了配准算法的研究和改进工作，针对传统迭代最近点算法(ICP)在建图过程中，在点云进行配准过程中使用点到点的配准方式，导致点云配准耗时长，容易产生误差造成点云配准精度低的问题，提出了一种对ICP算法改进的方案。该方法在点云数据预处理方面，通过降采样和特征点提取，减少了点云配准时间。在点云帧间配准中，将传统ICP算法点到点寻找对应点集的配准方式改为点到线和点到面的方式进行点云配准，最终获取激光雷达的运动估计。通过多个实验与其他配准算法进行对比，得出该方法基于多线激光雷达能够有效构建点云地图，利用点到线和点到平面的约束关系改善了传统迭代最近点算法误匹配的弱点，减少了点云配准时间，具有良好的配准精度。

基金项目

国家重点研发计划资助(2021YFB2501800)；天津市技术创新引导专项(基金)21YDTPJC00130。