基于格上的一次群签名方案

Lattice-Based Primary Group Signature Scheme

摘要: 传统的签名方案大多基于离散对数困难问题和大整数的素数分解问题，不能抵抗量子计算的攻击。针对此问题，本文基于格上ISIS困难问题，提出了一种新的一次群签名方案，并证明了方案的正确性、签名的不可伪造性、签名者的匿名性。新方案只需要密码杂凑算法的计算，具有更高的效率。

Abstract: Traditional signature schemes are mostly based on discrete logarithmic hard problems and prime factorization problems of large integers, which cannot resist the attack of quantum computing. Aiming at this problem, this paper proposes a new primary group signature scheme based on the difficult problem of ISIS on the lattice, and proves the correctness of the scheme, the unforgeability of the signature and the anonymity of the signer. The new scheme only needs the calculation of the cryptographic hash algorithm and has higher efficiency.

1. 引言

1991年，Chaum等人 [1] 提出了群签名方案。群签名方案允许群中的任一合法成员都可以代表群对消息进行匿名签名，在验证的过程中，只需要群公钥，同时签名不可伪造。如果需要进一步确定签名者身份，需要群管理员用追踪密钥找出签名者并核实其身份信息。群签名的这些特征，使得它在电子货币、电子商务、电子投票等领域得到很好地应用。一次性签名作为一种特殊的签名方式，其原理是基于无陷门单向密码杂凑函数对输入的消息进行签名。签名的安全性取决于密码杂凑函数安全。因此，一次签名方案具有较高的安全性和签名生成、验证的效率。本文一次群签名是在群签名的过程中暴露部分私钥。每签名一次更换一次密钥，来保证签名的绝对安全性。

随着量子计算的飞速发展，传统群签名方案的安全性受到了严重威胁，例如基于RSA、ElGamal、ECC等公钥密码体制的群签名方案 [2] [3]。因此，急需研究设计能够抵御量子计算机攻击的群签名方案。基于格上的一次群签名算法方案具有效率高、抗量子计算机攻击等特点，成为当前后量子密码算法研究热点之一。

1979年，Lamport [4] 等人提出了一种基于单向函数的一次数字签名方案。由此引出了利用单向密码杂凑算法进行数字签名的研究，但由于该方案中需要存储大量的密钥，使得该方案在实际应用中受限。2010年，Dov Gordon、Katz和Vaikuntanathan在亚洲密码学会上第一次提出基于错误学习问题(LWE)设计的基于格的群签名方案 [5] (简称GKV方案)。然而，GKV方案在防止陷害攻击方面存在缺陷，其中，群管理员会盗用合法群成员进行签名，并且不能有效地管理群成员的加入和退出，使得签名的长度会随着群成员的增加而增长。2013年，Laguillaumie、Langlois、Libert和Stehlé在亚洲密码学会上对基于格的群签名方案进行了改进 [6]，该方案解决了群签名长度随成员个数快速增长的问题，使得群成员个数与群签名长度满足对数关系。但是，该方案中采取加解密来设计追踪机制，使得签名效率大大降低，同时，还需要满足“加密方案”是安全的。2015年，Nguyen、Jiang Zhang和Zhenfeng Zhang为了使签名长度摆脱全成员的依赖，提出了基于LWE和小整数解问题(SIS)的格上群签名方案 [7]，然而，该签名方案不能有效地管理群成员的加入和退出，在防止陷害攻击方面仍存在漏洞。2006年，Zhou等人提出了一种基于混沌的Hash函数，可以极大地提高数字签名的安全性能 [8]。然而，该方案依赖RSA公钥密码体制，数字签名仍存在依赖大整数分解的困难性，在量子计算机的时代，无法抵抗后量子时代的量子攻击。在最近设计的基于格的群签名方案中 [9] [10] [11] [12] [13]，仍然存在随着群成员的个数的增多，签名长度也在快速增加的问题。

本文针对上述问题，结合基于格上ISIS困难问题，提出了一个新的基于格上的一次群签名方案。该方案在整个算法的设计中用到了格的One-Way Function (OWF)，在签名密钥和群公钥产生的过程中，通过哈希函数来计算，并将一次性签名融入其中，能够抵抗已知攻击，其安全性是利用哈希函数的单向性来保障，因为安全的哈希函数会有更多次扩散和混淆，原理是通过循环迭代一种特殊的结构使其更加安全，能抵抗量子计算的攻击。

2. 格上的困难问题

本文所设计的一次群签名方案是基于格上的困难问题，为便于理解，本节首先介绍格上的一些基本概念和安全模型。

设共有m个线性无关的向量 $v_1,v_2,\cdots ,v_m\in R^n$，产生的集合： $\wedge \left(v_1,v_2,\cdots ,v_m\right)=\left\{\underset{i=1}{\overset{m}{{\displaystyle \sum }}}{t}_i{v}_i|t_i\in Z\right\}$ 称为格。

LWE (Learning With Error)问题：已知整数 $n,m\ge n,q>2$，矩阵 $A\in Z_q^{n\times m}$，向量 $v\in Z_q^n$，概率分布 $\chi m$，向量e服从 $Z_q^m$ 上的分布 $\chi m$，则可分为两类：

1) 搜索版本的LWE：基于等式 $v^t=s^{t}A+e^t$，找到s的值。

2) 判定版本的LWE：判定 $v^t$ 是均匀选取的还是由公式 $v^t=s^{t}A+e^t$ 计算得出的。

SIS问题(Small Integer Solutions Problem)：我们可以根据已知条件 $q\in Z,\beta \in R,A\in Z_q^{n\times m}$，找到一个向量(非0) $v\in Z^m$，使得等式 $Av=0\mathrm{mod}q$ 成立，并且满足条件 $\Vert v\Vert \le \beta$。

ISIS问题(Inhomogeneous Minimum Integer Solution Problem)：已知 $q\in Z,\beta \in R,A\in Z_q^{n\times m}$，向量 $u\in Z_q^n$，可以找到非零向量 $v\in Z^m$，使得 $Av=u\mathrm{mod}q$，并且 $\Vert v\Vert \le \beta$。

这个单向函数(OWF)的构造如下。首先，我们随机选取一个 $n\times m$ 阶的矩阵 $A\in {\mathbb{Z}}_q^{n\times m}$，然后，我们这个OWF的输入就是一个二进制向量 $x\in {\left\{0,1\right\}}^m$。这个OWF的输出则是： $f_A\left(x\right)=Ax\mathrm{mod}q$。记 $H=f_A\left(x\right)=Ax\mathrm{mod}q$。

2.1. 格上选择明文攻击(CPA)模型

现在的数字签名方案中，很多的学者利用Chosen-Plaintext Attack (CPA)模型来证明其方案的安全性。

CPA是一种典型的攻击模型。在限定的时间内，攻击者F会随机选择消息，通过询问随机预言机O来获得对消息的签名，并通过刚刚拿到的签名来构造一个合法的消息签名 $\left(M^{\prime },{\sigma }^{M^{\prime }}\right)$。其中，图1展示了该过程。伪造者F给随机预言机O发送消息集合 $\left(M^1,M^2,\cdots ,M^n\right)$，随机预言机将得到的签名集合 $\left({\sigma }^1,{\sigma }^2,\cdots ,{\sigma }^n\right)$ 再发送给F。通过这些签名集合，F可以伪造一个消息–签名对 $\left(M^{\prime },{\sigma }^{M^{\prime }}\right)$。如果 ${\sigma }^{M^{\prime }}$ 是合法的，并且消息 $M^{\prime }$ 不在询问的消息中，则F伪造成功。CPA-Secure-Model模型原理是利用伪造者F成功的概率极小，并且这个概率可以忽略不计。

Figure 1. CPA model diagram

图1. CPA模型图

2.2. 格上非交互零知识证明

在2013年，基于ISIS问题的一个零知识证明被Lauillaumie等提出，只需要一个Fiat-Shamir转换，就能得到一个ISIS关系的非交互零知识证明(NIZKP)： $R_{ISIS}=\left\{\left(A,y,\beta ,x\right)|\exists x\in Z_q^m,Ax=y\mathrm{mod}q,\Vert x\Vert \le \beta \right\}$，这里， $A\in Z_q^{n\times m},y\in Z_q^m,\beta \in R$。

3. 基于ISIS群签名方案的设计

本文选取基于格上的哈希函数，提出了一种基于格上的一次群签名方案。该方案不仅在生成消息摘要的过程中使用哈希函数，而且在生成密钥算法、签名算法和验证算法中都是依赖此哈希函数。

3.1. 签名密钥的产生

假设群中有m ( $m\ge 2$ )个群成员，群中每个成员选取n个二进制向量 $g_k{}_i\in {\left\{0,1\right\}}^n$， $\left(1\le k\le m,1\le i\le n\right)$，令 $X_k=\left(g_{k_1},g_{k_2},\cdots ,g_{k_n}\right)$，那么， $X_k$ 为成员k的签名私钥。

3.2. 群公钥产生

对于群中每个成员，计算n个二进制向量私钥的哈希值，并进行异或计算得到代表自己身份的 $B_k$，即 $B_k=H\left(g_{k_1}\right)\oplus H\left(g_{k_2}\right)\oplus \cdots \oplus H\left(g_{k_n}\right)\left(1\le k\le m\right)$，其中，H为哈希运算。然后，这m个群成员分别将自己的 $B_k$ 通过安全信道传输给可信第三方(TA)，这样，TA将得到m个n维二进制向量 $B_1,B_2,\cdots ,B_m$。TA将收到的 $B_1,B_2,\cdots ,B_m$ 进行异或并求哈希得到群公钥 $C_k=H\left(B_1\oplus B_2\oplus \cdots \oplus B_m\right)$。

3.3. 签名过程

群中的所有成员都可以对消息进行签名，若由第k个成员进行签名，则签名过程如下：

假设消息为 $M\in {\left\{0,1\right\}}^{*}$，计算消息M的摘要 $d=\left(d_1,d_2,\cdots ,d_n\right)$，其中， $d_i\in {\left\{0,1\right\}}^n$。

第k个成员将表示自己身份的 $B_k$ 发送给TA，TA通过群成员的身份集 $\left(B_1,B_2,\cdots ,B_m\right)$ 验证他是否为合法的群成员里的一员。如果未通过，直接丢弃该请求；若验证通过，被判定为群内一员，TA计算 $Y_k={\displaystyle \underset{j\ne k}{\sum }\oplus B_j}$ 并将 $Y_k$ 发送给该成员k。该群成员根据自己的签名密钥和可信第三方发送过来的 $Y_k$ 对消息进行签名。

具体签名过程如下：

当 $d_i$ 向量中的0的个数大于 $n-m$ 的时候，记 $d_i={\left\{0\right\}}^n$，此时 $g_{k_i}$ 保持不变；否则 $d_i={\left\{1\right\}}^n$，求出 $g_{k_i}$ 对应的Hash值 $H\left(g_{k_i}\right)$。在 $n+1$ 的位置将 $Y_k$ 添加到签名中。

那么，对消息M的签名 $S=\left\{s_1,s_2,\cdots ,s_n,Y_k\right\}{\in }^{\left\{n+1,m\right\}}$，其中：

$s_i=\{\begin{array}{l}{g}_{k_i}{d}_i={\left\{0\right\}}^n\hfill \\ H\left(g_{k_i}\right)d_i={\left\{1\right\}}^n\hfill \end{array}\left(1\le i\le n\right)$。

3.4. 验证过程

验证者收到群签名后，首先计算消息M的摘要 $d=\left(d_1,d_2,\cdots ,d_n\right)$。然后利用群公钥 $C_k$ 对收到的签名 $S=\left\{s_1,s_2,\cdots ,s_n,Y_k\right\}$ 进行验证。

首先，计算 $P=\left(P_1\oplus P_2\oplus \cdots \oplus P_n\oplus Y_k\right)$，其中：

$p_i=\{\begin{array}{l}H\left(s_i\right)d_i=\left\{0\right\}\hfill \\ s_i{d}_i=\left\{1\right\}\hfill \end{array}\left(1\le i\le n\right)$。

计算 $H\left(P\right)\oplus C_k$ 的值是否等于 $0\in {\left\{0\right\}}^n$。若相等，则认为得到的签名消息有效，否则无效，说明该签名为非法签名。

具体的签名和验证过程如图2所示。

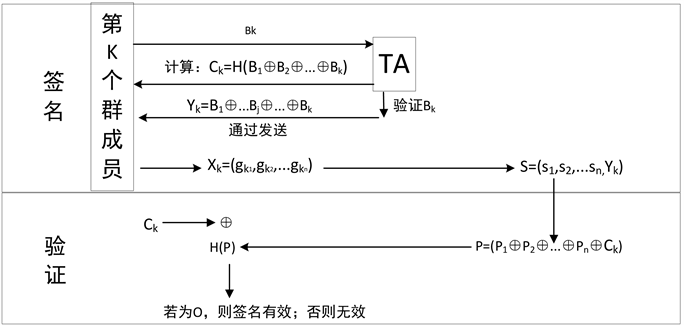
Figure 2. Signing and verification process

图2. 签名和验证过程

下面对上述签名方案的正确性进行证明。

事实上，由上述签名过程知，当 $d_i={\left\{0\right\}}^n$ 时， $p_i=H\left(s_i\right)=H\left(g_{k_i}\right)$ ；当 $d_i={\left\{1\right\}}^n$ 时， $p_i=s_i=H\left(g_{k_i}\right)$。

所以，

$H\left(P\right)=H\left(P_1\oplus P_2\oplus \cdots \oplus P_n\oplus Y_k\right)=H\left(H\left(g_{k_1}\right)\oplus H\left(g_{k_2}\right)\oplus \cdots \oplus H\left(g_{k_n}\right)\right)$。

又因为，群公钥为 $C_k=H\left(B_1\oplus B_2\oplus \cdots \oplus B_m\right)=H\left(H\left(g_{k_1}\right)\oplus H\left(g_{k_2}\right)\oplus \cdots \oplus H\left(g_{k_n}\right)\right)$。

所以，可以得出 $H\left(P\right)\oplus C_k=0$。明显，上述签名验证是正确的。

4. 安全性分析

4.1. 不可否认性

在得到对消息M的群签名 $S=\left\{s_1,s_2,\cdots ,s_n,Y_k\right\}$ 后，如果想知道群中谁完成了此次签名，只需要可信第三方TA计算 $p_i=\{\begin{array}{l}H\left(s_i\right)d_i={\left\{0\right\}}^n\hfill \\ s_i{d}_i={\left\{1\right\}}^n\hfill \end{array}\left(1\le i\le n\right)$，从而计算 $B_k=P_1\oplus P_2\oplus \cdots \oplus P_n$，TA通过 $B_k$ 和存储的每个群成员的签名密钥的哈希值，就能确定该签名人员，因此，本方案具有不可否认性。

4.2. 不可伪造性

在第2.1节中我们介绍了CPA安全模型，在此基础上，本节将描述本文方案具备不可伪造性。本文首先，假设存在一个伪造者F，假设伪造者F只知道公钥 $C_k$，并且只能对一条消息的签名进行询问。

定理1在CPA安全模型下，该方案具有不可伪造性。令 $t_{ow}$， ${\epsilon }_{ow}$ 为正实数，让 $G=\left\{H:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^n\right\}$ 是 $\left(t_{ow},{\epsilon }_{ow}\right)$ 个单向函数族。在使用G的CPA模型和 $\left(t_{OTS},{\epsilon }_{OTS},1\right)$ 参数下，满足 ${\epsilon }_{OTS}\le 4n{\epsilon }_{OW}$ 和 $t_{OTS}=t_{OW}-t_{SIG}-t_{GEN}$，其中， $t_{GEN}$ 和 $t_{SIG}$ 分别为密钥生成和签名时间。

本节只需证明底层哈希函数是一个单向哈希函数，即本文在CPA模型下存在不可伪造性，即将证明安全性规约为底层哈希函数的安全性。

在伪造者F只知道公钥 $C_k$，随机预言机(O)能够获取新的密钥对 $\left(sk,pk\right)$ 的前提下，伪造者F会向O询问消息M的合法签名，当收到来自随机预言机返回的签名 $s_i^M$ 时，F再将试图构造一个合法的消息–签名对 $\left(M^{\prime },s_i^{M^{\prime }}\right)$，必须满足签名 $s_i^{M\text{'}}$ 合法，且 $M\ne M^{\prime }$。如果在有限时间t内，伪造者F能成功构建消息－签名对的概率不大于 $\epsilon$，则说明我们的签名方案在CPA安全模型下不可伪造，记为 $\left(t,\epsilon ,1\right)-EU$。

攻击者以均匀分布随机选择索引 $a\in \left\{1,\cdots ,n\right\}$ 和 $b\in {\left\{0,1\right\}}^m$。他将矩阵 $y_a\left[b\right]$ 替换为目标矩阵y。接下来， $Ad{v}_{OTS}$ 使用修改后的公钥运行伪造F。如果伪造者要求其预言机签署消息M的摘要 $d=\left(d_1,d_2,\cdots ,d_n\right)$，并且如果 $d_a=1-b$，则攻击者扮演预言机的角色，签署消息并返回签名。攻击者可以签署这条消息，因为他知道原始密钥对，并且由于 $d_a=1-b$，公钥中修改后的向量没有被使用。但是，如果 $d_a=b$，则对手无法签署M。所以他对预言机查询的回答是失败，这也导致伪造者中止。如果伪造者的预言机查询成功，或者伪造者根本没有询问预言机，伪造者可能会产生伪造消息 $M^{\prime }$ 和签名 $s_i^{M^{\prime }}$。如果 ${d^{\prime }}_a=b$，则 $s_a^{M^{\prime }}$ 是攻击者返回y的原像。否则，对手返回失败。正是描述如算法1：

我们现在计算攻击者 $Ad{v}_{OTS}$ 的成功概率。我们用表示伪造者成功的概率，用表示它的运行时间，通过 $t_{GEN}$ 和 $t_{SIG}$，我们分别表示方案中生成密钥和签名所需的时间。当且仅当F使用消息M和 $d_a=1-b$ 查询预言机时，对手 $Ad{v}_{OTS}$ 可以成功地找到y的原像，或者如果他根本不查询预言机，如果伪造者返回消息 $M^{\prime }$ 的有效签名，其中 ${d^{\prime }}_a=b$。由于b是均匀分布的随机选择，因此， $d_a=1-b$ 的概率为 $\frac{1}{2}$。由于 $M^{\prime }$ 必须与查询的消息M不同，因此，至少存在一个索引c使得 ${d^{\prime }}_c=1-d_c$。如果c=a， $Ad{v}_{OTS}$ 成功的概率至少为 $\frac{1}{2n}$。因此，攻击者在时间 $t_{OW}=t+t_{SIG}+t_{GEN}$ 中找到原像的成功概率至少为 $\frac{\epsilon }{4n}$。证毕。

因此， $Ad{v}_{OTS}$ 在时间 $t_{OTS}$ 内能成功构建消息－签名对 $\left(M^{\prime },s_i^{M^{\prime }}\right)$ 的概率不大于 ${\epsilon }_{OTS}$，这也能看出该方案的安全性可规约为底层哈希函数的单向性。

4.3. 匿名性

定理2在随机预言机模型下，本方案在LWE假设下是CPA-匿名的。

证明：通过游戏 $G_0$ 、 $G_1$ 证明。

$G_0$ ：挑战者依据本方案得到群公钥 $C_k=H\left(B_1\oplus B_2\oplus \cdots \oplus B_m\right)$ 、成员私钥 $X_k$，并将 $\left(X_k,C_k\right)$ 发送给敌手，从 $\left\{1,\cdots ,m\right\}$ 中随机选择两个身份标识 $i_1,i_2$，并记 $i_0\leftarrow \left\{i_1,i_2\right\}$，并以身份 $i_0$ 按照本方案对消息M进行签名，得到 $S^{\prime }=\left\{{s^{\prime }}_1,{s^{\prime }}_2,\cdots ,{s^{\prime }}_n{Y}_k\right\}$，并将该签名发送给敌手。

$G_1$ ：与 $G_0$ 一样，除了用NIZKP生成。依据NIZKP性质可知， $G_0$ 和 $G_1$ 在计算上不可取分。

综上所述，在随机预言机模型下，本方案在LWE假设下是CPA-匿名的。

5. 结束语

在当代密码学研究中，量子发展迅速，后量子时代数字签名算法已经变得不可或缺。本文基于格上的哈希函数设计了一种一次群签名方案，相比较于传统的RSA、ECC等公约密码体制建立的数字签名，可以有效地抵抗量子攻击。与已有的签名方案相比，本文是基于格上的一次性签名方案，可以获得更高的效率。相信在未来，随着后量子计算机的发展，传统的签名算法将逐步被淘汰，而抗量子的这些签名算法将会成为主流，尤其今年NIST将后量子数字签名算法SPHINCS⁺推荐进入第四轮行业标准的评估，抗量子的算法进一步得到发展。下一步将基于格的一次性环签名，进一步解决密钥太大的问题。

基金项目

国家自然科学基金(61370188)；北京市教委科研计划(KM202010015009)；北京市教委科研计划资助(No. KM202110015004)；北京印刷学院博士启动金项目(27170120003/020)；北京印刷学院科研创新团队项目(Eb202101)；北京印刷学院校内学科建设项目(21090121021)；北京印刷学院重点教改项目(22150121033/009)；北京印刷学院科研基础研究一般项目(Ec202201)。