信息隐藏技术概述及实现可逆信息隐藏的代价分析

Overview of Information Hiding Technology and Cost Analysis of Realizing Reversible Information Hiding

摘要: 作为信息安全保护和版权保护的重要手段，信息隐藏技术在20世纪后得到了迅速发展，目前可大致分为两种类型：可逆信息隐藏和不可逆信息隐藏。本文总结了信息隐藏技术及其发展脉络，并对多种信息隐藏算法进行性能分析，就三种不可逆算法——LSB算法、NEC算法、DCT算法，和两种可逆算法——像素直方图平移算法、相邻像素差构造直方图算法，共五种算法采用定量分析方式进行算法性能的探究，并对五种算法的不可感知性、鲁棒性和信息容量进行纵向比较，探究实现可逆信息隐藏的代价。

Abstract: As a necessary approach of information security and copyright protection, information hiding technology has developed rapidly since the 20th century, and can be roughly divided into two types: reversible information hiding and irreversible information hiding. The paper summarizes the information hiding technology and its development, and mainly analysis the performance of five information hiding algorithm, which contain three kinds of irreversible algorithm-the LSB algorithm, NEC and DCT algorithm, and two reversible algorithmpixel histogram translation algorithm, adjacent pixel difference histogram construction algorithm. In this paper, quantitative analysis is adopted to compare the performance of the algorithms by longitudinal measurement of imperceptibility, robustness and information capacity, and explore the cost of realizing reversible information hiding.

1. 信息隐藏的概述及其发展

信息隐藏或数据隐藏是一种把有意义的信息隐藏在另一个称为公开载体(如文本、图像、声音及视频)的信息中得到隐蔽载体，非法者不知道这个普通信息中是否隐藏了其他的信息，即使知道也难以提取或去除隐藏的信息的方法 [1]。信息隐藏主要由隐密术和数字水印技术构成。

隐密术是利用人类感官系统的不敏感性，将隐秘信息以某种方式隐藏在特定的信息载体中，使之不易察觉，即通过掩盖信息本身来传递真实信息 [2]。

相较于隐密术，数字水印更有发展和探究空间，本文主要就数字水印的发展及其迭代的各种算法进行分析。

数字水印是20世纪90年代出现的一门技术，是一种将特定的数字信息(如身份信息、序列号、文字或图像标志等)嵌入到图像、音频、视频或软件等各种数字产品中，以达到信息安全和版权保护等目的的技术 [3]。数字水印技术弥补了密码编码学中无法对解密后信息进行进一步保护的不足，还满足了数字签名技术中一次性嵌入大量数据的需求，是一种有效保护数字版权的方法。数字水印技术大体可分为两种类型：可逆数字水印和非可逆数字水印。

非可逆数字水印比较有代表性的是空间域方法，例如1994年Schyndel等人提出的LSB (Least Significant Bit最低有效位)算法，直接将像素点数值的二进制位最低位作为隐藏位置，用秘密信息替换原值，这种方法操作简单快速，对原始图像的改变很小，不可感知性很好，但会对原始图像造成永久的破坏，并且由于使用了图像不重要的像素位，算法的鲁棒性差，水印信息很容易被破坏。基于此，Cox等人提出一种将空间域图像变换至DCT变换域后再嵌入秘密信息的方法，即NEC算法。其实现方法是，首先以密钥为种子来产生伪随机序列，该序列具有高斯N(0, 1)分布 [4]；其次对图像做DCT变换，最后用伪随机高斯序列来调制(叠加)该图像除直流(DC)分量外的1000个最大的DCT系数 [4]。通过修改部分系数，Cox等人发现，为满足水印的不可见性，将水印嵌入DCT变换域的交流(AC)高频系数更加合适；但若需要保证鲁棒性，则DC低频系数作为嵌入点更加合适。为解决水印不可见性和鲁棒性之间的矛盾，1997年Cox等人提出了DCT算法。DCT算法是第一个基于扩频思想的数字水印算法，它以NEC算法为基础，并借鉴了通信中的扩频技术，先把图像分割成小块，再把水印信息嵌入到图像的DC低频系数中，同时舍弃部分AC高频系。

可逆数字水印是指在载体图像内嵌入一个特定的信息，该信息能够在需要的时候被完整地提取出来，同时载体图像能够在提取出该特定信息后被完全复原。该技术能够满足对图像进行认证，或在其中隐藏信息的目的。对于可逆数字水印算法，可大致分为两类——基于直方图的数字水印算法和基于误差预测的数字水印算法。

2006年，Ni等人提出了一种基于直方图的可逆信息隐藏算法，即通过改变零值点和峰值点之间的像素在峰值点附近构造零值点，并将0-1比特流分别嵌入峰值点和构造出的零值点所对应的像素值中，从而达到嵌入水印的目的。这种方法实现了数字水印的可逆恢复，该算法依旧存在两个问题：一是像素直方图算法的嵌入容量受限于峰值点个数，因此该算法的嵌入容量十分有限；二是嵌入数据后直方图的峰值点会发生明显变化。2009年，Tai等人提出了相邻像素差构造直方图进而嵌入数据的方法，并应用像素差值二叉树，使每个差值通过二叉树规律扩展后的像素值不会重复，从而保证了提取数据时可以根据二叉树将像素值恢复原状，且扩大了嵌入容量。但这种二叉树使数据的嵌入对图像造成的失帧大，嵌入数据后的图像质量有所损伤。之后提出的“高保真直方图平移算法”则是对于峰值点变化问题起到了一定的改善作用。该算法不直接用峰值点作为嵌入点，而是选择满足一定条件的点P的集合C(P)进行水印嵌入。但对于上述基于直方图的算法而言，均未考虑像素之间的相关性，零值点是否存在，以及峰值–零值点对是否重叠等问题。

针对上述问题，在基于误差预测的数字水印算法中得到了一定改善。在基于误差预测的数字水印算法中，残差直方图算法结合了直方图算法与误差预测技术。该算法将图像分为不重叠的块，用线性预测器求出每一块的残差，进而求出残差的多对峰值–零值点，然后嵌入信息，并利用线性逆变换得到携带秘密信息的图像。该算法解决了像素之间存在相关性，零值点不存在以及峰值–零值点对可能重叠等问题，且针对重叠和不重叠的峰值–零值点对有不同的嵌入规则，但复杂算法不可避免的会带来图像失帧更大的问题，同时，预测的不准确性也会对嵌入效果带来一定影响。

2. 衡量算法性能的三个指标

2.1. 不可感知性

不可感知性是指嵌入信息后，原始图像质量仍旧保持良好且视觉效果未有明显变化的特性。不可感知性是信息隐藏的前提和基础。如果这一特性不达标，就失去了“隐藏”的根本意义。

在信息隐藏领域中，定量度量信息隐藏的不可感知性的客观指标主要是峰值信噪比(PSNR)和均方误差(MSE) [5]。对于一个 $m\times n$ 像素的灰度图像，假设原始载体图像和嵌入信息后的载体图像每个像素的值分别为 $f\left(i,j\right)$ 和 $g\left(i,j\right)$，其中 $i\in [1,m],j\in [1,n]$，图像的PSNR和MSE值分别有公式：

$\text{PSNR}=10{\log }_{10}\left(\frac{\max f{\left(i,j\right)}^2}{\frac{1}{mn}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\left(f\left(i,j\right)-g\left(i,j\right)\right)}^2}}}\right)$ (1)

$\text{MSE}=\frac{1}{mn}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\left(f\left(i,j\right)-g\left(i,j\right)\right)}^2}}$ (2)

由于8位灰度图像最大值为255，则PSNR可表示为：

$\text{PSNR}=10{\log }_{10}\left(\frac{{255}^2}{\text{MSE}}\right)$ (3)

需要注意的是，MSE和PSNR值的变化基于 $f\left(i,j\right)-g\left(i,j\right)$ 的变化。

由式(1) (2)可知，当原图像F与嵌入信息后的图像G越相似，则像素差值 $f\left(i,j\right)-g\left(i,j\right)$ 就越小，MSE的值就越小，PSNR的值就越大。即不可感知性和PSNR的值成正比。PSNR值高于40dB说明图像质量极好，非常接近原始图像，其在30~40 dB范围通常表示图像质量是好的(即图像稍有失帧，可以察觉，但处于可接受范围内) [6]。本文将通过设置同等增幅的隐写量对比PSNR值来评价五种数字水印算法的其不可感知性。

2.2. 鲁棒性

数字水印的鲁棒性是指嵌入信息的载体在传输处理等过程中经历了一些无法避免的损伤(如编码压缩、解码还原等)，或是遭到一些刻意攻击之后，仍能从载体中正确提取水印的能力 [7]。

本文将通过在不同强度的噪声影响下提取出的水印信息的BER值(错误比特率)来评价五种数字水印算法的鲁棒性。

关于衡量标准，通过分析大量文献，我们可以认为：当BER值低于15%时，该算法具有鲁棒性。

2.3. 信息容量

信息容量是指在保证数字水印完整、正确的基础上，原始载体单次可嵌入的水印信息的最多比特。信息容量越大越好，这样能一次性让载体隐藏更多的信息。

本文将对比五种数字水印算法的信息容量。

3. 定量分析方式下五种数字水印算法的分析及对比

实验采用的原始载体图像均为 $512\times 512$ 的灰度图像lena.bmp。

3.1. LSB算法

3.1.1. LSB算法的实现

LSB全称为 Least Significant Bit(最低有效位)，是一种常被用做图片隐写的算法，属于空间域算法中的一种。当采用 $512\times 512$ 的灰度图像作为嵌入信息的载体时，灰度化的图像为单通道格式存储像素，每个像素值在0~255内，即00000000~11111111。把每个像素的相同位抽取出来组成一个新的平面，就是图的位平面。位平面越高，包含的原图像信息越多，对图像的灰度值贡献越大，并且相邻比特的相关性越强，反之相反。与最低位平面相关的几乎都是图片中的随机噪点，基本上不包含图像具体信息。因此，可以在最低位平面嵌入水印或秘密信息，即LSB算法原理。

3.1.2. LSB算法性能分析

1) 不可感知性

读取灰度图像“lena.bmp”，并将其转化为二维像素值数组；在上述LSB算法的基础上，定义psnr函数，探究不同隐写量前提下PSNR值的变化。

需要注意的是，由于在LSB算法中仅在每一像素点的最低位嵌入一个比特的信息量，因此PSNR值取决于嵌入秘密信息的长度。我们将嵌入秘密信息的长度与载体像素点个数的比值称为隐写量，用来表示每像素所占存储空间的比特位数，基本单位是bits per pixel (bpp)，通常情况下，隐写量设置为0.4 bpp或者更低。秘密信息长度和隐写量成正比。本实验设置隐写量范围为0.01~0.09 bpp (即秘密信息长度范围为2621~23,593)。

当隐写量范围在0.01~0.09 bpp之间时，计算出的PSNR值如表1所示。

可以看出，PSNR值均大于40dB，意味着LSB的不可感知性较好。但随着嵌入信息量(即隐写量)的不断增大，PSNR值也在逐渐减小。

Table 1. PSNR values of LSB under different embedding information sizes

表1. LSB在不同嵌入信息量大小下的PSNR值

2) 信息容量

由于在LSB算法中仅在每一像素点的最低位嵌入一个比特的信息量，故LSB的满嵌率为 $512\times 512$，即262,144 bit。并且，当嵌入信息量达到最大极限时，PSNR值为51.1548 dB，也可得出LSB的不可感知性较好。

3) 鲁棒性

对使用LCB算法嵌入秘密信息的图像添加不同强度的高斯噪声，分别提取加噪前和加噪后图像中的秘密信息，计算BER值。结果如表2所示。

Table 2. BER value of LSB under different intensity Gaussian noise

表2. LSB在不同强度高斯噪声影响下的BER值

由于LSB算法的NC值大于0.9818，且在一定噪声的影响下，BER值始终小于15%，因此，LSB算法的鲁棒性较好。

针对上述实验结果可以看出，随着嵌入容量的增大，尽管算法的不可感知性在迅速减弱，但当达到最大嵌入容量时，其PSNR值仍大于40 dB，确保了图像的不可感知性。同时在不同程度高斯噪声的影响下，BER值仍然维持较低水平，因此我们可以认为，LSB算法的不可感知性和鲁棒性都达到较好水平。但不可否认的是，LSB算法的嵌入容量受到了极大的限制，难以实现对较大型数据文件的隐写。

3.2. NEC算法

3.2.1. NEC算法的实现

该算法首先将密钥作为种子用于产生伪随机序列，该序列具有高斯N(0, 1)分布的特征 [8]；其次对图像做DCT变换，最后用伪随机高斯序列来调制(叠加)该图像除直流(DC)分量外的N个最大的DCT系数 [5]。本实验中采用的二维DCT变换就是将二维图像从空间域转换到频率域。

实验对图像数据进行二维的DCT变换，在得到的频率域中寻找最大的N个DCT系数index来携带水印信息W，并根据公式 $I_i=X_i{\left(1+\alpha W\right)}_i$ 得到含水印的DCT系数I (其中 $\alpha$ 是尺度因子，用于控制嵌入强度，本实验取 $\alpha =0.1$ )。最后进行二维逆DCT变换，并将像素灰度值进行截断使其值位于[0, 255]之间，从而得到含水印的图像。

3.2.2. NEC算法性能分析

1) 不可感知性

通过计算嵌入不同量级信息前后图像的PSNR值，结果如表3所示。

可以发现，嵌入不同量级的信息量，NEC的PSNR值变化平稳，但始终维持在较低水平。由于PSNR值高于40 dB才证明图像有较好的不可感知性，因此可以看出，NEC算法的不可感知性较为逊色。

Table 3. PSNR value of NEC under different embedding information sizes

表3. NEC在不同嵌入信息量大小下的PSNR值

2) 信息容量

理想状态下，满嵌率可达到1 bpp，即262,144 bit。此时的PSNR值为37.2284 dB。

3) 鲁棒性

对使用NEC算法嵌入秘密信息的图像添加不同强度的高斯噪声，分别提取加噪前和加噪后图像中的秘密信息，计算BER值。结果如表4所示。

Table 4. BER value of NEC under different intensity Gaussian noise

表4. NEC在不同强度高斯噪声影响下的BER值

可以发现，在不同强度的高斯噪声影响下，对于BER值，较低程度的噪声对于隐藏信息的提取几乎没有影响，当噪声强度达到0.1时，仅有0.1%的信息受到影响。因此，NEC算法的鲁棒性很强。通过对大量文献的总结可以得知，NEC算法的鲁棒性非常强，在遭到一般性的攻击(如缩放、剪切、JPEG压缩等)时影响不大，经过一系列操作后仍然可以将水印从图像中提取出来 [9]。表5为NEC算法在不同水印攻击下检出隐秘信息的情况。

Table 5. NEC algorithm detects secret information under different attacks

表5. NEC算法在不同攻击下检出隐秘信息的情况

3.3. DCT算法

3.3.1. DCT算法的实现

DCT算法在NEC算法的基础上进行了改进，已解决其不可感知性较弱的问题。DCT算法同样是在频率域上进行隐藏操作。DCT算法先在空间域上进行图像的分割，将图像分割为若干个 $8\times 8$ 的块，对每一块进行DCT变换后再将水印信息嵌入到图像的DC低频系数中。

对于分割后的一个 $8\times 8$ 小块，DCT算法规定对该块进行DCT变换，然后分别选择变换后图像中的两个位置(这里用 $\left(u_1,v_1\right)$ 和 $\left(u_2,v_2\right)$ 代表所选定的两个系数的坐标)，进行以下操作。

对于一串二进制比特流：

1) 如果 $B_i\left(u_1,v_1\right)>B_i\left(u_2,v_2\right)$，代表隐藏1：如果相反，则交换两系数；

2) 如果 $B_i\left(u_1,v_1\right)<B_i\left(u_2,v_2\right)$，代表隐藏0；如果相反，则交换两系数；

关于系数的选择需要注意，如果选择的两系数相差较大，则对图像的影响较大，因此应选择相近的值(如中频系数)。

3.3.2. DCT算法性能分析

1) 不可感知性

对嵌入了0.01~0.09 bpp大小的数据量的图像进行实验，所得的PSNR值如表6所示。

Table 6. PSNR values of DCT under different embedding information sizes

表6. DCT在不同嵌入信息量大小下的PSNR值

可以发现，相对与NEC算法而言，DCT算法的不可感知性有了极大的提升。同时，随着隐写量的增加，PSNR值没有大幅度改变，保留了NEC算法在不可感知方面较为稳定的特性。

2) 信息容量

理想状态下，满嵌率可达到1 bpp，即262,144 bit。

3) 鲁棒性

该方法根据NEC算法改进得来，故保留了NEC算法强鲁棒性的特征。同样对嵌入信息后的图像进行高斯噪声水印攻击后，再提取隐藏信息，结果如表7所示。

Table 7. BER value of DCT under different intensity Gaussian noise

表7. DCT在不同强度高斯噪声影响下的BER值

可以看出，DCT算法的鲁棒性同NEC相似，该算法具有较强的抗干扰能力，在较强的高斯噪声影响下，其错误比特率始终维持在极低水平

3.4. 像素直方图平移算法

3.4.1. 像素直方图平移算法的实现

像素直方图平移算法是一种给基于图像像素直方图的的可逆信息隐藏算法。它通过改变零值点和峰值点之间的像素在峰值点附近构造零值点，并将0~1比特流分别嵌入峰值点和构造出的零值点所对应的像素值中，从而达到嵌入水印的目的。该算法实现了数字水印的可逆恢复。实现像素直方图平移算法的步骤如下：

a) 将图像像素值转换为像素直方图；

b) 选定直方图的峰值和离峰值最近的零值点；

c) 将峰值点和零值点之间的像素值向左(若零值点在峰值点左侧)或向右(若零值点在峰值点右侧)平移一个单位，在峰值点旁创造一个嵌入空间；

d) 若构造出的新的零值点在峰值点左侧(即c中像素值左移)，此时，依次扫描图像各像素点的像素值，若某点像素值等于峰值且需要嵌入的秘密信息为1，则该像素值−1；若想嵌入0，则该像素值维持不变。反之，若构造出的新零值点在峰值点右侧(即c中像素值右移)，在扫描图像各像素点像素值后，若某点像素值等于峰值且需要嵌入的秘密信息为1，则该像素值+1；若想嵌入0，则像素值保持不变。

3.4.2. 像素直方图平移算法性能分析

1) 信息容量

像素直方图算法的嵌入容量受限于峰值点个数。在本实验使用的原始图像条件下，最大嵌入容量仅有5056 bit，此时PSNR值为59.3220 dB。

2) 不可感知性

通过信息容量分析得知，最大嵌入容量为5056 bit，因此在对PSNR进行分析时，选择嵌入数据量范围在0.001~0.013 bpp之间的图像进行实验，所得的PSNR值如表8所示：

Table 8. PSNR values of pixel histogram translation algorithm under different embedding information sizes

表8. 像素直方图平移算法在不同嵌入信息量大小下的PSNR值

可以发现，随着嵌入容量的增大，PSNR值未发生明显改变且均高于40 dB。因此像素直方图算法的不可感知性较强且十分稳定。

3) 鲁棒性

对图像进行不同强度高斯噪声的干扰后，提取图像的秘密信息并与原秘密信息进行比对，得到的BER值如表9所示。

Table 9. BER value of pixel histogram translation algorithm under different intensity Gaussian noise

表9. 像素直方图平移算法在不同强度高斯噪声影响下的BER值

可以发现，在强度为0.5的噪声影响下，依旧可以准确提取书出秘密信息。说明像素直方图平移算法具有极强的鲁棒性。

3.5. 相邻像素差构造直方图算法

3.5.1. 相邻像素差构造直方图算法的实现

为扩大嵌入容量，Ni等人提出了利用多对峰值—零值点组合进行信息隐藏，但该方法在进行提取恢复时需要知道各组合之间峰值—零值点的对应方式，因此对于发送方而言，会增加发送方需要传输的数据量。并且，一旦该数据被截获，则会造成水印信息的泄露，存在一定的安全隐患。

基于以上种种，Tai提出了一种相邻像素差值构造直方图算法，该算法同时还提高了嵌入容量。具体实现步骤如下：

a) 将二维像素矩阵按照S型顺序进行扫描，连接成一个一维数组；

b) 计算数组中相邻像素的差的绝对值，以此确定像素差直方图以及其峰值P；

c) 再次扫描图像，对于差值大于P的像素进行平移，对于差值等于P的像素进行数据的嵌入，最后得到携密图像；

d) 使用同样的P值进行信息提取；

e) 最后恢复原始图像。

为扩大嵌入容量，可在原方案的基础上利用多个峰值点来隐藏数据。改进后的方案利用一棵完全二叉树来传递峰值点信息。在图1的二叉树中，每个节点代表一个差值。若差值小于2^L，嵌入0，访问左子树；嵌入1，则访问右子树。若差值大于等于2^L，则将像素平移2^L。其中，L是二叉树的高度。这样，发送方只需要传输二叉树的高度L。

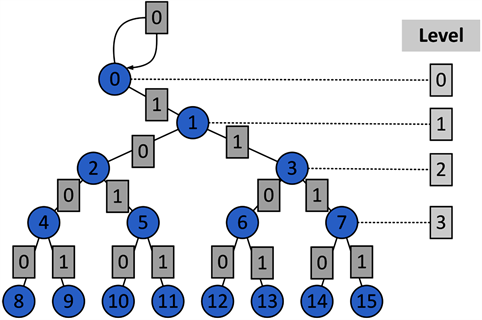
Figure1. Pixel adjacent difference binary tree

图1. 像素相邻差二叉树

3.5.2. 相邻像素差构造直方图算法性能分析

1) 不可感知性

对嵌入了0.01~0.09 bpp大小的数据量的图像进行实验，所得的PSNR值如表10所示：

Table 10. PSNR value of histogram algorithm constructed by adjacent pixel difference under different embedding information size

表10. 相邻像素差构造直方图算法在不同嵌入信息量大小下的PSNR值

可以看出，该算法的PSNR值虽然不高，但依旧大于40%，说明在秘密信息长度较小时，相邻像素差构造直方图算法依旧有较强的不可感知性。

2) 信息容量

本算法的最大嵌入信息容量与设定的二叉树深度L值有关。深度L、最大嵌入容量和相应PSNR值如表11所示：

Table 11. Different L corresponds to the maximum embedding capacity and its PSNR value

表11. 不同的L对应的最大嵌入容量及其PSNR值

3) 鲁棒性

分别提取加噪前和加噪后图像中的秘密信息，计算BER值。数据见表12：

Table 12. BER value of adjacent pixel difference histogram translation algorithm under different intensity Gaussian noise

表12. 相邻像素差直方图平移算法在不同强度高斯噪声影响下的BER值

4. 数据分析

综合上述实验结果，可以得到表13、表14和表15。

4.1. PSNR

分析PSNR表格可以发现，非可逆算法的不可感知性要远强于可逆算法的不可感知性(NEC算法除外)。这是因为，可逆算法为达到可逆的目的，需要使用更为复杂的算法，而更复杂的算法带来的是图像改变的增大，进而造成图像失帧严重。因此，图像不可感知性变差是实现可逆的代价之一。

Table 13. PSNR values of five algorithms with different embedding capacities

表13. 五种算法在不同嵌入容量下的PSNR值

4.2. 最大嵌入容量

在同等PSNR水平和BER水平的前提下，可以发现，非可逆算法的嵌入容量要远大于可逆算法的嵌入容量。尽管像素差直方图平移算法可以达到较大的嵌入容量，但其不可感知性不能维持较高水平。由此可见，为实现可逆，算法需要更多的嵌入空间来保证算法的可逆性，留给信息嵌入的空间将不可避免的减少。因而，嵌入容量也是实现可逆的代价之一。

Table 14. Maximum embedding capacity of five algorithms

表14. 五种算法的最大嵌入容量

4.3. 鲁棒性

根据实验结果，该实验所涉及的三种非可逆算法均有较好的鲁棒性，其错误比特率在较强噪声的干扰下依旧能处于较低水平。对于两种可逆算法来说，在相同程度的噪声影响下，相邻像素差直方图平移算法的BER值远大于15%，而直方图平移算法的BER值趋近于0。造成该种差异的原因主要是两者的嵌入容量相差较大。直方图平移算法的嵌入容量仅有5056 bit，而相邻像素差直方图平移算法的嵌入容量能达到甚至超过非可逆算法的最大嵌入容量。由此可以看出，鲁棒性也是实现可逆信息隐藏的代价之一。对于可逆算法而言，衡量水印算法的三个指标：不可感知性，嵌入容量和鲁棒性之间是相互制约的关系。

Table 15. BER values of five algorithms under different noise intensities

表15. 五种算法在不同噪声强度干扰下的BER值