1. 引言
研究响应变量和解释变量之间的关系是统计分析中重要的一部分,在研究中通常建立回归函数来解释这种关系。在生存分析或可靠性研究中经常会遇到右删失数据,因此有大量的文献研究右删失数据的非参数模型。本文中记解释变量为X,响应变量为Y,T为未受到删失的变量,C为删失变量,观测样本记
,
,此处
以及
,
为集合A的示性函数。在一般情况下,删失变量C与解释变量和响应变量
并不是独立的,但在给定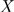 的情况下,C与T条件独立,即
的情况下,C与T条件独立,即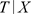 与
与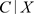 独立。
独立。
在非参数统计推断领域中,条件密度函数的估计不仅在给定解释变量时对响应变量的预测发挥着重要作用,并且它是探索解释与响应变量之间所有关系的基本工具。Tjøstheim (1994) [1] 和Polonik and Yao (2000) [2] 对条件密度函数进行直接估计。Hyndman et al. (1996) [3] 中提出了条件密度的核估计方法。Hyndman和Yao (2002) [4] 提出了对于条件密度估计中选择平滑系数简单且有效的方法。Gooijer和Zerom (2003) [5] 的Nadaraya-Watson估计量。但这些文章中所研究的都是完整的观测值,删失变量的非参数估计可以回溯到Kaplan和Meier (1958) [6] 提出T的生存函数,之后多位学者证明了此估计量的弱收敛性、一致收敛速度等性质。在Beran (1981) [7] 了在右删失数据下条件密度函数的非参数回归估计估计量。Gonzalez (1994) [8] 此估计量的一些渐近性质及应用。Khardani和Semmar (2014) [9] 在C与
独立情况下非参数条件密度函数核估计,但其对
和
的独立性假设太强。因此,本文将其独立性假设放松为
和给定
的
之间的独立性假设。
本文研究的主要目的是当响应变量Y为右删失数据时,构造条件密度函数的非参数估计量,证明估计量的一致强相合性并得出收敛速度。在第二节中,给出本文构造的条件密度函数估计量;第三节中给出本文用到的假设及主要结论,并给出证明;最后对构造的估计量进行模拟,计算其估计误差来验证估计效果。
2. 估计量的构造
考虑n对定义在
上的独立随机变量
,
为独立同分布的删失随机变量,且服从未知连续分布函数G。当假设
与
独立时,删失变量的生存函数估计量在Kaplan和Meier (1958) [6] 中被定义为
本文考虑在响应变量
是右删失时,研究给定
时T的非参数条件密度估计。删失变量的条件生存函数在Gonzalez (1994) [8] 中构造的一致收敛到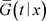 的估计量被定义为
的估计量被定义为
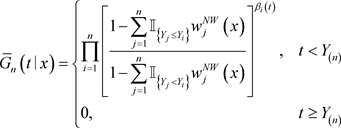 (1)
(1)
此处
,
。
对于
的观测值
,本文定义条件密度函数 的非参数估计为
的非参数估计为
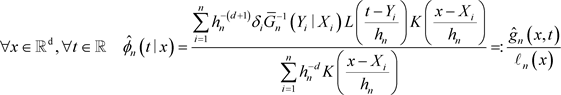 (2)
(2)
此处
,
。
3. 假设与主要结论
3.1. 假设
本文定义
和
分别为T和C的分布函数且,
和
为生存函数
和
的上端点,假设
并且C与T条件独立,即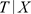 与
与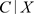 独立。我们假设存在一个紧集
,此处的
是解释变量X的边缘密度函数,
也是一个紧集使得
。对于平滑系数h,我们设定
。在推导中为了方便表示,将M定义为任意的正常数。
独立。我们假设存在一个紧集
,此处的
是解释变量X的边缘密度函数,
也是一个紧集使得
。对于平滑系数h,我们设定
。在推导中为了方便表示,将M定义为任意的正常数。
假设A. 核函数K和L是Lipschitz连续函数并且满足紧支撑,且对所有的
,
,有
(3)
假设B.
1) X的边缘密度函数
二阶可微且满足Lipschitz条件,对所有的
且
,有
。
2)
的联合密度函数为
有界函数且二阶可导。
假设C.
1) 数列
满足
。
2) 对一些
,有
。
3.2. 一致强相合性及收敛速度
定理3.1. 在假设A,B和C下,得到
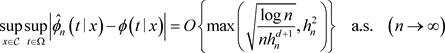
证明:令
定理3.1的证明在以下分解的基础上进行
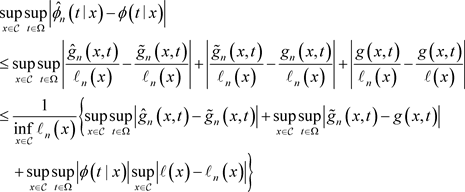 (4)
(4)
引理3.2. 在假设A,B (2)和C下,可以得到
引理3.3. 在假设A,B (1)和C下,可以得到
引理3.4. 在假设A,B (2)和C下,可以得到
4. 模拟
在这一部分中通过计算均方误差来观察估计量
的估计效果。本文利用R语言生成
的n组随机数,其中解释变量
,
,其中
,
,其中
,则我们可以获得n组观测值
,此处
以及
。
Spierdijk (2008) [10] 中利用期望删失数据比例来计算
,使得可以借助
来控制删失数据率。在本节模拟中设定删失数据率分别为10%,30%,50%,计算后
。这与Kim (2010) [11] 中的设定相似。
在计算中
和
均使用Gaussian核函数,估计量的均方误差计算公式为
删失比例分别为10%、30%和50%的情况下估计量的最小均方误差如表1所示。在计算过程中,我们生成取值在
上,间隔为0.01的平滑系数,计算出使得估计量均方误差最小的平滑系数。从表1可以看出,随着删失比例的下降或样本容量的增加,估计量的最小均方误差减小,这与我们的预期相符,因为删失比例的下降或样本容量的增加意味着数据信息的增加。

Table 1. Minimum MSEs of estimator in the different censored rate
表1. 不同删失比例下估计量的最小均方误差
5. 中间结果的证明
5.1. 引理3.2的证明
证明:此处将其分解为两个部分
(5)
首先来证明
由于
,对于所有的可测函数
以及所有的
,有
因此可以得到
由
以及
,有
通过换元
,并将g在
处泰勒展开
由假设可知
于是有
因此,
现在,证明另一部分
对任意的
和
,根据
和
选取k和j,由于集合
和
的紧集性质,对于
和
,有
和
其中
和
并且
。
在这个部分中,将其依照如下分解来分别证明
(6)
首先对于
:运用核函数L的Lipschitzian条件可以得到
由假设可知
是紧支撑的,并且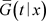 是删失变量的生存函数,则
与
是删失变量的生存函数,则
与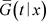 均为有界,因此
均为有界,因此
由假设有
下面对于
之后同理可得
下面对于
之后同理可得
之后对于
同理可得
最后对
进行证明,对所有的
,令
由于核函数K和L以及
均为有界函数,则有
以及
在此简要介绍Berstein不等式Hoeffding (1994) [12] (式2.13):
为X的独立样本,
,
,
,M为常数,且
,则
(7)
其中对于所有的
,有
。
因此,使用Berstein不等式,对于所有的
有
现在,令
,则对于任意的
可以得到
接下来利用
,可以得到
因此,选取合适的
使得
收敛,并且运用Borel-Cantelli引理可以得到
引理3.2证得。
5.2. 引理3.3的证明
证明:首先,将其分解为两部分
(8)
第一部分
与引理3.2类似,即
对于
同样借助核函数K的Lipschitzian条件,可得
由引理3.2证明中对
的设定,可以得到
对于
同样可以得到
因此,
部分同引理3.2的最后一部分证明,可以得到
对于本引理的第二部分,同样借助泰勒展开,得到
则可以得到
引理3.3证得。
5.3. 引理3.4的证明
证明:我们有
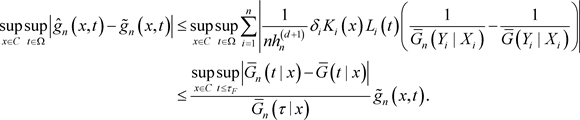 (9)
(9)
又由于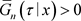 且
有界,可以得到
且
有界,可以得到
根据Gonzalez (1994) [8] 中结论有
(10)
引理3.4得证。
6. 结论
在众多文献中对数据的独立性进行了较强的假设,即假设C与
独立,但在实际观测到的数据中其只能满足条件独立的假设。因此本文考虑在右删失数据与未受到删失影响的数据条件独立的情况下,构建了具有一致强相合性的条件密度函数的非参数估计量,并计算其收敛速度。本文在构造非参数估计量时用到了经典的Nadaraya-Watson核估计,对于其他核估计,例如能够减少边界效应的局部线性回归核估计,所构成的非参数估计量将在未来的工作中被讨论。